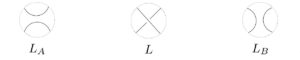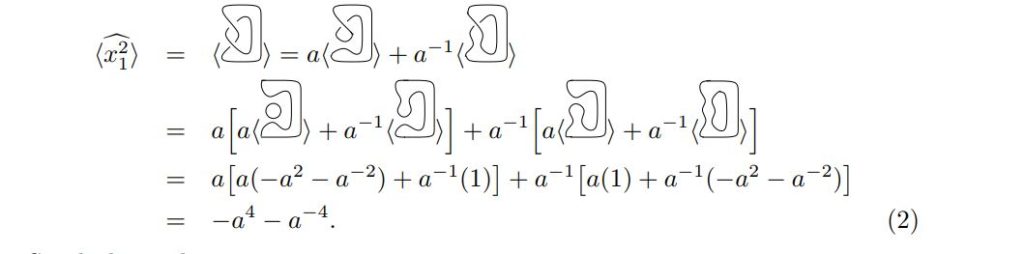Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2017.0008
Kauffman Bracket of 2- and 3-Strand Braid Links
Abdul Rauf Nizami\(^1\)
Abdus Salam School of Mathematical Sciences, Government College University, Pakistan. (A.R.N)
\(^{1}\)Corresponding Author: arnizami@sms.edu.pk
Abstract
Keywords:
1. Introduction
The Kauffman bracket was introduced by L. H. Kauffman in 1987 in [1]. The Kauffman bracket (polynomial) is actually not a knot invariant because it is not invariant under the first Reidemeister move. However, it has many applications and it can be extended to the popular Jones polynomial, which is invariant under all three Reidemeister moves. In the present work we shall confine ourselves to the Kauffman bracket to avoid from unnecessary length and to leave it for applications. In [2] Nizami et al, computed Khavanov Homology of Braid Links and in [3] gave recursive form of Kauffman Bracket. This paper is organized as follows: In Section 2 we shall give the basic ideas about knots, braids, and the Kauffman bracket. In Section 3 we shall present the main results.2. Preliminary Notions
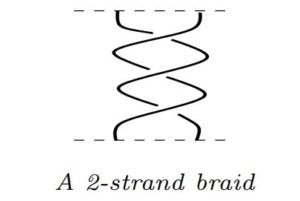
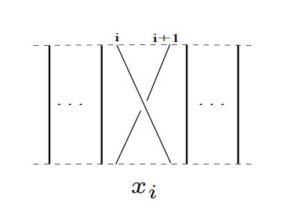
2.1. Links. A link is a disjoint union of circles embedded in \(\mathbb{R}^{3}\). A one-component link is called a knot. Links are usually studied via projecting them on a plan; a projection with extra information of overcrossing and undercrossing is called the link diagram.2.2 Braids. Braids were first studied by Emil Artin in 1925 [5, 6], which play an important role in knot theory, see [7, 8] for detail. An \(n\)-strand braid is a set of \(n\) non intersecting smooth paths connecting \(n\) points on a horizontal plane to \(n\) points exactly below them on another horizontal plane in an arbitrary order. The smooth paths are called strands of the braid.
Remark 2.1. In the last section we shall present all the links as closures of products of elementary braids.
2.3. The Kauffman Bracket The Kauffman bracket was introduced by Kauffman in [10]. Before the definition it is better to understand the two types of splitting of a crossing, the \(A\)-type and the \(B\)-type splittings:Definition 2.1 The Kauffman bracket is the function \(\langle \cdot\rangle: \mbox{Links}\rightarrow \mathbb{Z}[a,a^{-1}]\) defined by the axioms: \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \langle L\rangle &=& a\langle L_{A} \rangle + a^{-1} \langle L_{B} \rangle \\ \langle L \sqcup \bigcirc\rangle &=& (-a^{2} - a^{-2} )\langle L \rangle \\ \langle \bigcirc\rangle &=& 1 \end{eqnarray*} Here \(L\), \(L_{A}\), and \(L_{B}\) are three links which are isotopic everywhere except at one crossing where the look as in the figure:
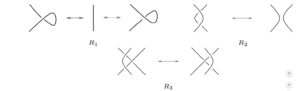
Proposition 2.2. The Kauffman polynomial is invariant under second and third Reidemeister moves but not under the first Reidemeister move.
3. Main Results
In this section we shall give the Kauffman bracket of the links \(\widehat{x_{1}^{n}}\) and \(\widehat{x_{1}^{b}x_{2}^{m}}\), and show that \(\langle\widehat{x_{1}^{b}x_{2}^{m}}\rangle=\langle\widehat{x_{1}^{b}}\rangle\langle\widehat{x_{2}^{m}}\rangle\).
The links \(\widehat{x_{1}^{n}}\) fall into two categories, the two-component links when \(n\) is even and the one-component links (means knots) when \(n\) is odd. When \(n\) is even, we have:Proposition 3.1. The Kauffman bracket of the link \(\widehat{x_{1}^{n}}\), when \(n\geq2\) is even, is
Proof.
We prove it by induction on \(n\).
When \(n = 2\),
Proposition 3.2. The Kauffman bracket of the knots \(\widehat{x_{1}^{n}}\), when \(n\) is odd, is
Proof. Similar to the proof of Proposition 3.1.
Proposition 3.3. The Kauffman bracket of the braid link \(\widehat{x_{1}^{b} x_{2}^{b}}\), when \(b\) is even, is \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \langle \widehat{x_{1}^{b} x_{2}^{b}} \rangle &=& \sum_{i=1}^{b-1}i(-1)^{i+1}a^{6b-4i}+\sum_{i=1}^{b}(-1)^{i+1}(b-i)a^{2b-4i}-(b-2)a^{2b}\\ &&+a^{4-2b}+a^{-2b-4}. \end{eqnarray*}
Proof. We prove it by induction on \(b\). When \(b = 2\), we have
Similarly, we get
Proposition 3.4. The Kauffman bracket of the braid link \(\widehat{x_{1}^{b} x_{2}^{b}}\), when \(b\) is odd, is \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \langle \widehat{x_{1}^{b} x_{2}^{b}} \rangle &=& \sum_{i=1}^{b-1}i(-1)^{i+1}a^{6b-4i}+\sum_{i=1}^{b}(-1)^{i}(b-i)a^{2b-4i}+(b-2)a^{2b}\\ &&+a^{4-2b}+a^{-2b-4}. \end{eqnarray*}
Proof. Similar to the proof of proposition 3.3.
Proposition 3.5. The Kauffman bracket of \(\widehat{x_{1}^{b} x_{2}^{m}}\), when \(b>m\geq2\), is \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \langle \widehat{x_{1}^{b} x_{2}^{m}} \rangle &=& \sum_{i=1}^{m-1}(-1)^{b+m+1-i}(i)a^{3(b+m)-4i}+(-1)^{b+1}(m-1)a^{3b-m}\\ &&+m\sum_{i=1}^{b-m-1}(-1)^{b+1-i}a^{3b-m-4i}+(-1)^{m+1}(m-1)a^{-b+3m}\\ &&+\sum_{i=1}^{m-2}(-1)^{m+1-i}(m-i)a^{-b+3m-4i}+2a^{-b-m+4}+a^{-b-m-4}. \end{eqnarray*}
Proof.
We first verify the result for arbitrary \(b\) and \(m=2\):
Resolving all \(2^{3+2}\) crossings as were resolved for \(\langle \widehat{x_{1}^{2} x_{2}^{2}} \rangle\) in Proposition 3.3, we get
\begin{eqnarray*}
% \nonumber to remove numbering (before each equation)
\langle \widehat{x_{1}^{3} x_{2}^{2}} \rangle &=& -a^{11}+a^{7}-a^{3}+2a^{-1}+a^{-9}
\end{eqnarray*}
Similarly, we get
Theorem 3.6. For any \(b,m\geq2\), $$\langle \widehat{x_{1}^{b} x_{2}^{m}} \rangle = \langle \widehat{x_{1}^{b}} \rangle \langle \widehat{x_{1}^{m}} \rangle.$$
Proof.
Depending on \(b\) and \(m\), the proof is divided into three cases: when \(b,m\) are even and equal, when \(b,m\) are odd and equal, and when \(b,m\) are distinct.
Case I. (When \(b\) and \(m\) are even and equal.)
In this case, letting \(m=b\), we show that \(\langle \widehat{x_{1}^{b} x_{2}^{m}} \rangle = \langle \widehat{x_{1}^{b}} \rangle \langle \widehat{x_{1}^{m}} \rangle.\) So, we proceed as follows:
\begin{eqnarray*}
% \nonumber to remove numbering (before each equation)
\langle \widehat{x_{1}^{2} x_{2}^{2}} \rangle &=& a^{8} + 2 + a^{-8}= (-a^{4}-a^{-4})(-a^{4}-a^{-4})=\langle \widehat{x_{1}^{2}} \rangle \langle \widehat{x_{1}^{2}} \rangle.
\end{eqnarray*}
Also, we have
\begin{eqnarray*}
% \nonumber to remove numbering (before each equation)
\langle \widehat{x_{1}^{4} x_{2}^{4}} \rangle &=& a^{20}-2a^{16}+3a^{12}-2a^{8}+3a^{4}-2+2a^{-4}+a^{-12} \\
&=& (-a^{10}+a^{6}-a^{2}-a^{-6})(-a^{10}+a^{6}-a^{2}-a^{-6})\\
&=& \langle \widehat{x_{1}^{4}} \rangle \langle \widehat{x_{1}^{4}} \rangle
\end{eqnarray*}
and
\begin{eqnarray*}
% \nonumber to remove numbering (before each equation)
\langle \widehat{x_{1}^{6} x_{2}^{6}} \rangle &=& a^{32}-2a^{28}+3a^{24}-4a^{20}+5a^{16}-4a^{12}+5a^{8}-4a^{4}\\
&&+3-2a^{-4}+2a^{-8}+a^{-16} \\
&=& (-a^{16}+a^{12}-a^{8}+a^{4}-a^{0}-a^{-8})(-a^{16}+a^{12}-a^{8}\\
&&+a^{4}-a^{0}-a^{-8})=\langle \widehat{x_{1}^{6}} \rangle \langle \widehat{x_{1}^{6}} \rangle.
\end{eqnarray*}
Now we assume that the result is true for \(b=k\), that is
$$\langle \widehat{x_{1}^{k} x_{2}^{k}} \rangle = \langle \widehat{x_{1}^{k}} \rangle \langle \widehat{x_{1}^{k}} \rangle.$$
Since
\(\langle \widehat{x_{1}^{n}} \rangle = -a^{3(n)-2} + a^{3(n)-6} + a^{-2}(\langle \widehat{x_{1}^{n-2}} \rangle)\), we have
Case II. (When \(b\) and \(m\) are odd and equal.) Similar to Case I.
Case III. (When \(b\) and \(m\) are distinct.)
In order to prove this part let us agree on the terminology: \begin{eqnarray*} % \nonumber to remove numbering (before each equation) \overline{x}_{n} &=& (-1)^{m+n}a^{3m-(4n-2)}, n=1,2,\ldots,m-1, \overline{x}_{m}=-a^{-m-2}\\ \overline{y}_{l} &=& (-1)^{b+l}a^{3b-(4l-2)}, l=1,2,\ldots,b-1, \overline{y}_{b}=-a^{-b-2}\\ i&=&1,2,\ldots,m, j=1,2,\ldots,b; b\geq2\\ \end{eqnarray*} \begin{eqnarray*} % \nonumber to remove numbering (before each equation) &&\langle \widehat{x_{1}^{b}} \rangle \langle \widehat{x_{1}^{m}}\rangle \\ &=&\sum_{i+j=2}^{m}\overline{x}_{i}\overline{y}_{j}+\sum_{i+j=m+1, i\neq m}\overline{x}_{i}\overline{y}_{j}+\Big[\sum_{i+j=m+2, i\neq m}\overline{x}_{i}\overline{y}_{j}+\overline{x}_{m}\overline{y}_{1}\\ &&+\sum_{i+j=m+3, i\neq m}\overline{x}_{i}\overline{y}_{j}+\overline{x}_{m}\overline{y}_{2}+\cdots+\sum_{i+j=b, i\neq m}\overline{x}_{i}\overline{y}_{j}+\overline{x}_{m}\overline{y}_{b-m-1}\Big]\\ &&+\Big[\sum_{i+j=b+1, i\neq 1,m}\overline{x}_{i}\overline{y}_{j}+\overline{x}_{m}\overline{y}_{b-m}\Big]+ \Big[\Big(\sum_{i+j=b+2, i\neq 2,m}\overline{x}_{i}\overline{y}_{j}+\overline{x}_{m}\overline{y}_{b-m+1}+\overline{x}_{1}\overline{y}_{b}\Big)\\ &&+\Big(\sum_{i+j=b+3, i\neq 3,m}\overline{x}_{i}\overline{y}_{j}+\overline{x}_{m}\overline{y}_{b-m+2}+\overline{x}_{2}\overline{y}_{b}\Big)+\cdots\\ &&+\Big(\sum_{i+j=b+m-3, i\neq m-3,m}\overline{x}_{i}\overline{y}_{j}+\overline{x}_{m}\overline{y}_{b-4}+\overline{x}_{m-4}\overline{y}_{b}\Big)\\ &&+\Big(\overline{x}_{m-1}\overline{y}_{b-1}+\overline{x}_{m}\overline{y}_{b-3}+\overline{x}_{m-3}\overline{y}_{b}\Big) +\Big(\overline{x}_{m}\overline{y}_{b-2}+\overline{x}_{m-2}\overline{y}_{b}\Big)\Big]\\ &&+\Big(\overline{x}_{m}\overline{y}_{b-1}+\overline{x}_{m-1}\overline{y}_{b}\Big)+\overline{x}_{m}\overline{y}_{b} \end{eqnarray*} Since this agrees with the result of Proposition 3.5, the proof is finished.
Competing Interests
The author(s) do not have any competing interests in the manuscript.References
- Kauffman, L. H. (1987). State models and the Jones polynomial. Topology, 26(3), 395-407. [Google Scholor]
- Nizami, A. R., Munir, M., Sohail, T., & Usman, A. (2016). On the Khovanov Homology of 2-and 3-Strand Braid Links. Advances in Pure Mathematics, 6(06), 481-491. [Google Scholor]
- Nizami, A. R., Munir, M., Saleem, U., & Ramzan, A. (2014). A Recursive Approach to the Kauffman Bracket. Applied Mathematics, 5(17), 2746-2755.
- Reidemeister, K. (1948). Knot theory, Chelsea Publ. Co., New York.
- Artin, E. (1925, December). Theorie der z\(\ddot{o}\)pfe. In Abhandlungen aus dem Mathematischen Seminar der Universitt Hamburg (Vol. 4, No. 1, pp. 47-72). Springer Berlin/Heidelberg.
- Artin, E. (1947). Theory of braids. Annals of Mathematics, 101-126. [Google Scholor]
- Birman, J. S. (2016). Braids, Links, and Mapping Class Groups.(AM-82) (Vol. 82). Princeton University Press. [Google Scholor]
- Murasugi, K. (2007). Knot theory and its applications. Springer Science & Business Media. [Google Scholor]
- Alexander, J. W. (1923). A lemma on systems of knotted curves. Proceedings of the National Academy of Sciences, 9(3), 93-95. [Google Scholor]
- Kauffman, L. H. (1990). An invariant of regular isotopy. Transactions of the American Mathematical Society, 318(2), 417-471. [Google Scholor]