Box-Behnken design of quadratic model for Gas Metal Arc Welding (GMAW) and optimization analysis on desirability function

1. Introduction

In Gas Metal Arc Welding (GMAW), materials are melted and joined by heating them by an arc which is produced between filler wire which is continuously fed the metals. Arc is protected and shielded by using inert gases like Helium and Argon and because of this GMAW is also called Metal Inert Gas (MIG) process. Other than inert gases some active gases i.e. \(CO_{2}\) are used so GMAW is now the widely used name for this process. This is constant voltage process and Direct Current Electrode Positive (DCEN) is used in GMAW. Either Direct Current Electrode Positive (DCEN) or Alternating Current (AC) transfer of metal is unreliable. But here arc is a stable transfer of metal smoothly, low chances of spatters, and high penetration is worthy characteristics of this process [1, 2].

M. Azadi [3] studied the optimization of GMAW over API-X42 material through L36 Taguchi matrix and proposed back propagation neural network (BPNN). Omer Bataineh [4] studied the GMAW process to find the effects of welding factors over welding strength; the optimization was done through factorial design methodology and ANOVA. Izzatul [5] optimized the welding responses such as penetration, microstructural and hardness by utilizing robotic GMAW process. Pawan Kumar [6] studied the dissimilar welding joints welded by GMAW and optimized the result by Taguchi orthogonal L9 array and analysis was concluded based on the signal to noise ratios. Chandresh [7] worked with full factorial design experiment to optimize the GMAW responses on AISI 1020 material.

All above investigation and experimental study were conducted on GMAW process under a controlled environment such as well-established and equipped closed welding workshop whereas we have studied the semi-automatic GMAW performed under tough environmental conditions such as windy and dusty in the mobile or outdoor welding shop. Through data mining of field engineering on nominal identical data on which we have done field study and relevant data points are chosen. The portable welding shop is the shop which moves the location to location base on projects scope such as for cross-country pipeline.

2. Process Features and Parameters [1]

In the gas metal welding, arc regulation is auto-adjusted by any of two ways. The most known technique is to employ a constant-speed electrode feed unit with a variable current and constant voltage source. With the variation of gap between gun and work piece, the variation in arc length is also noted, where if arc length decrease power source gives more current and if arc length increases then of course less current. So there will be relevant changes in meting rate due to such changes in current which in turn require maintaining arc length. Other technique of arc regulation is to employ a constant-current source along with adjustable-speed, voltage-sensing electrode feeder. Here any change in arc length originates a relevant variation in the AC voltage. Based on the electrode feed unit changes the speed of filler metal wire depending upon higher/lower speed. This is more useful for larger electrodes when lower feed speed of filler metal wire is required. The GMAW setup used for the research work is depicted in Figure 1.

3. Design of Experiment Methodology [8, 9]

The factors can be classified as either continuous with low and high value or categorical with different level. We have selected continuous type of factors instead of the categorical type with minimum and maximum value because GMAW factor's values fluctuate frequently due to welding in the temporary welding shop. Design of experiment is done by selecting voltage (V), welding consumable feed speed (mm), and travel speed (cm/mm) as continuously controllable factors with low and high values as defined in Table 2. These controllable factor's effects are studied on four responses such as weld bead (mm), bead reinforcement height (mm), penetration depth (mm) and deposition efficiency(%). Each response is assigned with minimum and maximum values which are obtained from design condition for ASME B31.3 process piping for non-sour and non-lethal service and are mentioned in Table 1. The response's results are studied and analyzed on mean values basis and target to maximize the mean of the depth of penetration, deposition efficiency. The quantitative relation between responses and factors in term of Response Surface Methodology (RSM) can be expressed as below: \begin{equation*} Y = f( \text{Voltage, wire feed , travel speed}) \end{equation*} whereas \(Y\) is the responses which are to be optimized and \(V, F\) \& \(S\) are the controllable factors. The system behavior will be obtained through quadric model or by higher order polynomial model which is developed by the least square method by considering the interaction of factors to maximize or minimize the response variables, below is the quadratic model for author case: In Equation (1), the author designate betas as coefficient of linear, quadratic and interaction of input \(V\), \(F\), and \(T\). The \(\beta0\) is the intercept term whereas \(\beta1, \ \beta2, \ \beta3 \ and \ \beta11,\ \beta22, \ \beta33\) are the linear terms and interaction between variables terms respectively.

Table 1. Defining of controllable factors to be measured.

Name	Units	Type	Role	Low	High
A:Welding Voltage	V	Continuous	Controllable	29.0	34.2
B: Wire Feed Speed	mm	Continuous	Controllable	3.9	9.7
C:Welding Speed	mm/min	Continuous	Controllable	50.0	70.0

Table 2. Defining of responses to be varied.

Name	Units	Analyze	Goal	Impact	Sensitivity	Low	High
Depth of Penetration	mm	Mean	Maximize	3.0	Medium	4.5	6.0
Deposition Efficiency	%	Mean	Maximize	3.0	Medium	55.6	93.4
Bead Width	mm	Mean	Maximize	3.0	Medium	6.5	8.0
Bead Reinforcement	mm	Mean	Maximize	3.0	Medium	0.7	3.0

Design of experiment's run and the model was established by Box-Behnken design which was developed by George E. P. Box. Box-Behnken is one of the experimental strategies for RSM where each factor is placed at equally distributed values on at least three levels and it fit on the quadratic model the design is equidistant from the design center which is placed in last. Total 30 runs are designed with 3 center points per block. The Design of experiments (DOE) parameters are tabulated in Table 3 [8].

Table 3. Design of experiments for a gas metal arc welding process.

Type of  Factors	Design Type	Center points Per Block	CenterPoint Placement	Design is Randomized	Number of  Replicates	Total Runs	Total Blocks
Process	Box-Behnken design	3	Last	Yes	1	30	2

To fit the results of the experiment, the Quadratic model of factors interaction is used and below table is the statistical data collected from large data points of the mobile welding shop, 30 runs are collected and responses of each run are measured from actual testing in mechanical laboratory refer to Table 4 for detail. The welding was conducted on API 5L Gr. 70 (fine grain Normalized 19mm thickness) material with single bevel angle. Bevel angle was checked with Dye penetrant testing for any possible defects like crack etc. GMAW machine of model MAXI 505 was used for welding. Whereas reinforcement was measured by using Cambridge type welding gauge. The welding joint design is given below in Figure 2; (joint design and bead width and reinforcement height etc [2].)

The larger pool of field data for GMAW process is reported in Raw Data file by authors [9].

Table 4. GMAW data for optimization process.

Sr. No.	Factors			Responses
	F1	F2	F3	R1	R2	R3	R4
	Voltage	Wire Feed	Travel Speed	Depth of Penetration (mm)	Deposition Efficiency (%)	Bead Width (mm)	Weld Reinforcement (mm)
1	29	6.8	50.0	5	55.6	6.50	0.7
2	34.2	6.8	70.0	6	91.6	6.50	2.0
3	29	9.7	60.0	5	90	6.00	2.0
4	31.6	3.9	50.0	5.5	77	8.50	3.0
5	29	3.9	70.0	5	77	8.00	2.5
6	31.6	3.9	50.0	4.5	56	6.50	0.8
7	34.2	6.8	70.0	5.5	92.5	6.50	2.2
8	34.2	9.7	60.0	6	92	6.00	2.2
9	31.6	9.7	50.0	6.5	80	8.00	3.0
10	31.6	9.7	60.0	5.3	92.3	6.50	2.0
11	34.2	3.9	70.0	5.2	92.1	6.40	2.0
12	29	6.8	50.0	5.3	92.3	6.50	2.0
13	31.6	6.8	60.0	5	92.2	6.50	2.0
14	34.2	9.7	70.0	5.3	88.7	7.0	3.0
15	31.6	3.9	50.0	5.6	90.2	7.7	2.9
16	31.6	6.8	60.0	5.3	90.7	6.3	2.5
17	34.2	3.9	70.0	5.3	88.6	7.8	3.1
18	29	6.8	50.0	6.0	94.7	7.3	2.7
19	31.6	9.7	60.0	6.1	94.0	9.4	2.9
20	34.2	9.7	70.0	6.1	94.6	6.1	2.5
21	31.6	3.9	50.0	5.7	93.0	8.5	2.9
22	31.6	6.8	60.0	5.2	88.3	6.3	2.9
23	34.2	6.8	70.0	5.2	87.7	7.0	3.0
24	29	9.7	50.0	5.2	89.1	6.3	2.5
25	31.6	3.9	60.0	5.4	89.4	7.7	2.9
26	34.2	6.8	70.0	5.8	93.3	7.3	2.7
27	29	3.9	50.0	6.3	96.5	9.6	3.4
28	31.6	6.8	60.0	5.9	95.2	6.6	2.6
29	34.2	9.7	70.0	6.3	98.9	10.5	2.6
30	31.6	3.9	50.0	5.6	91.7	6.6	2.8

4. Analyze the Experiments Results [8]

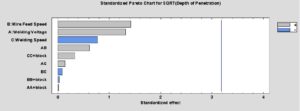
The variance's analysis is performed by Analysis of variance (ANOVA) was conducted to investigate the controllable factor's influences on measured responses then the standardized Pareto chart is drawn for each response with respect to significant factors. The analysis of variance is calculated for each of response and is explained in detail, refer below to Table 5 for depth of penetration, Table 6 for deposition efficiency, Table 7 for bead width and Table 8 for weld reinforcement height:

Table 5. Variance's analysis for SQRT of Depth of Penetratione.

Source	Sum of Squares	Dof	Mean Square	F-Ratio	P-Value
A:Welding Voltage	0.0330452	1	0.0330452	1.73	0.2799
B:Wire Feed Speed	0.0384051	1	0.0384051	2.01	0.2512
C:Welding Speed	0.0113129	1	0.0113129	0.59	0.4975
AA	0.00000229293	1	0.00000229293	0.00	0.9919
AB	0.00715199	1	0.00715199	0.37	0.5838
AC	0.00036437	1	0.00036437	0.02	0.8989
BB	0.0000164209	1	0.0000164209	0.00	0.9784
BC	0.000137468	1	0.000137468	0.01	0.9377
CC	0.0020654	1	0.0020654	0.11	0.7639
Total error	0.0572911	3	0.019097
Total (corr.)	0.150612	12

Table 5 is the variance analysis known as ANOVA where statistical significance is calculated by associating the experimental error with a mean square. The mean square value was obtained by computing the variability in Sq-Root (DOP) into a distinct run for each of the effects. In author occasion, no interactions of factors have P-values less than 0.05 which confirmed that all interactions are meaningfully diverse from "0" at the 95.0% confidence level.

The R-Squared calculation shows that the model as fitted illuminates 59.7% of the variability in Sq-Root (Depth of Penetration). The adjusted R-squared calculation is 39.55%, The standard error of the calculation indicates as 0.0871038.
The mean absolute error of 0.0590065 is the average value of the residuals.

Based on analysis of variance through ANOVA, the significant controllable factors are identified and then plotted against the standardized effect. Figure 3 shows that Wire Feed, welding voltage and their quadratic effect have a major effect on depth of penetration as compared to other factors. P-value for all interactions are greater than 5.0%.

Table 6. Variance's analysis for SQRT of Deposition Efficiency.

Source	Sum of Squares	Dof	Mean Square	F-Ratio	P-Value
A:Welding Voltage	1.16387	1	1.16387	2.45	0.2158
B:Wire Feed Speed	1.12495	1	1.12495	2.36	0.2217
C:Welding Speed	0.272031	1	0.272031	0.57	0.5045
AA	0.00838265	1	0.00838265	0.02	0.9028
AB	0.128551	1	0.128551	0.27	0.6391
AC	1.20742	1	1.20742	2.54	0.2094
BB	0.205795	1	0.205795	0.43	0.5577
BC	0.95518	1	0.95518	2.01	0.2515
CC	0.821663	1	0.821663	1.73	0.2802
Total error	1.42735	3	0.475783
Total (corr.)	7.44221	12

Table 6 is the variance analysis known as ANOVA where statistical significance is calculated by associating the experimental error with a mean square. The mean square value was obtained by computing the variability in Sq-Root (DOP) into a distinct run for each of the effects. In author occasion, No interactions of factors have P-values less than 0.05 which confirmed that all interactions are meaningfully diverse from “0” at the 95.0% confidence level. The R-Squared calculation shows that the model as fitted illuminates 80.82% of the variability in Sq-Root (Depth of Penetration). The adjusted R-squared calculation is 23.22%, The standard error of the calculation shows 0.689771 for the standard deviation of the residuals. The mean absolute error of 0.271215 is the average value of the residuals.

Based on analysis of variance through ANOVA, the significant controllable factors are identified and then plotted against the standardized effect. Figure 4 shows that quadric effect of Welding voltage and wire feed and wire feed and welding speed have a major effect on deposition efficiency as compared to other factors. P-value for all interactions is greater than 5.0%.

Table 7. Variance's analysis for SQRT of Bead Width.

Source	Sum of Squares	DOF	Mean Square	F-Ratio	P-Value
A:Welding Voltage	0.0111456	1	0.0111456	0.42	0.5650
B:Wire Feed Speed	0.037308	1	0.037308	1.39	0.3232
C:Welding Speed	0.0519844	1	0.0519844	1.94	0.2581
AA	0.0122513	1	0.0122513	0.46	0.5475
AB	0.0222912	1	0.0222912	0.83	0.4291
AC	0.0	1	0.0	0.00	1.0000
BB	0.0177043	1	0.0177043	0.66	0.4760
BC	0.00189437	1	0.00189437	0.07	0.8076
CC	0.0122513	1	0.0122513	0.46	0.5475
Total error	0.0804485	3	0.0268162
Total (corr.)	0.271784	12

The R-Squared calculation shows that the model as fitted illuminates 70.3999% of the variability in Sq-Root (Depth of Penetration). The adjusted R-squared calculation is 0.0%, which is appropriate for analyzing matrix with dissimilar number of independent variables. The estimated standard error for standard deviation of the residuals to be 0.163756. The mean absolute error of 0.0639226is the average value of the residuals.

Based on analysis of variance through ANOVA, the significant controllable factors are identified and then plotted against the standardized effect. Figure 5 shows that Welding speed and wire feed have a major effect on bead width as compared to other factors. There is no figure for serial autocorrelation in the residuals at significance level of 5.0% because P-value for interactions is greater than 5.0%.

Table 8. Variance's analysis for SQRT of Weld Reinforcement.

Source	Sum of Squares	DOF	Mean Square	F-Ratio	P-Value
A:Welding Voltage	0.0376313	1	0.0376313	0.24	0.6554
B:Wire Feed Speed	0.0222486	1	0.0222486	0.14	0.7295
C:Welding Speed	0.0523154	1	0.0523154	0.34	0.6013
AA	0.00538944	1	0.00538944	0.03	0.8637
AB	0.0139183	1	0.0139183	0.09	0.7836
AC	0.104516	1	0.104516	0.68	0.4709
BB	0.0264368	1	0.0264368	0.17	0.7068
BC	0.0675445	1	0.0675445	0.44	0.5556
CC	0.0141117	1	0.0141117	0.09	0.7821
Total error	0.46308	3	0.15436
Total (corr.)	0.841292	12

The R-Squared calculation shows that the model as fitted illuminates 44.9561% of the variability in Sq-Root (Depth of Penetration). The adjusted R-squared (the appropriate one) calculation is 0.0%, .The estimated standard error of the residuals to be 0.392887. The mean absolute error of 0.156633 is the average value of the residuals.

Based on analysis of variance through ANOVA, the significant controllable factors are identified and then plotted against the standardized effect. Figure 6 shows that Quadric effects of Welding voltage and welding speed have a major effect on bead width as compared to other factors.

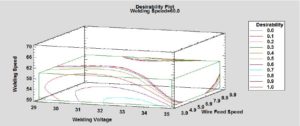
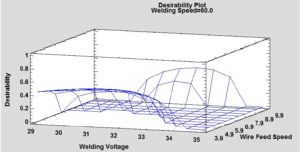
5. Optimization through Desirability-Function [8]

Optimum factors setting values are obtained through the value of optimized desirability which is obtained by considering the combined results of all five responses for specific predicted values. For optimization of response values, we have selected confident level of 95%. Whereas predicted values of each response is a mean value of upper 95% and lower 95% limit. Observed desirability is calculated from observed values of all response's values for each run of an experiment by using Derringer's model. Whereas predicted desirability is obtained from predicted values of all response base on lower and upper 95% limits of the confidence level.

6. Desirability Function [9, 10, 11 ]

The desirability function and loss function are used optimized approaches and we have used desirability function methodology because it is more applicability and flexibility as compared to loss function moreover it is a most suitable function to solve multi-objective optimization problems. As per definition is given by Harrington [9], "converts every response's value into scale-free value is known as desirability". The desirability function was also studied and shared by Derringer and Suich's [10] which is used for nominal-the best (NTB), larger-the-best (LTB), smaller-the-best (STB) type of measurable responses. In our DOE, we have selected the larger the best which is defined as: \[ d(i)= \begin{cases} 0, & yl \leq LSL_{i} \\ \frac{\hat{y}-USL_{i}}{LSL_{i}-USL_{i}}, & LSL \le \hat{y} \le USLi{i}\\ 1, & yl = USL_{i} \end{cases} \] Where \(d(i)\) is the desirability function, yet is the response, \(USL_{i}\) is the upper 95% limit and \(LSL_{i}\) is the lower 95% limits. Table 9 shows all calculation where responses are optimized by getting their prediction by taking the mean of lower 95.0% limits and upper 95.0% limit. Base on Derringer and Suich's desirability function as defined above, the desirability is calculated for depth of penetration, deposition efficiency, bead width, and bead reinforcement are 52.8%, 85.3%, 81.3% and 93.9% respectively [8]. The overall desirability or optimized desirability is equaled 77%, which is obtained by considering the desirability of all responses then taking each value to the power equal to its impact, taking the product of both results, and the resultant product raises to a power equal to 1 divided by impact summation.

Table 9. Optimum Response Values.

Response	Optimized	Prediction	Lower 95.0% Limit	Upper 95.0% Limit	Desirability
Depth of Penetration	yes	5.2921	3.47671	7.48744	0.528068
Deposition Efficiency	yes	87.8636	51.8112	133.382	0.853534
Bead Width	yes	7.72064	5.11714	10.8577	0.813758
Bead Reinforcement	yes	2.8614	0.204658	8.58927	0.939741

Optimized Desirability = 77%. Optimums setting of factors are obtained based on optimized desirability vs optimized responses values and are given in Table 10 and the graphical representation is mentioned in Figure 7.

Table 10. Factor settings at optimum.

Factor	Setting
Welding Voltage	33.2783
Wire Feed Speed	3.9
Welding Speed	60.0

The graphical presentation of optimal result shows in Figure 7 and Figure 8. Where within the model with respect to controllable welding variables desirability zone are marked in different color, blue color zone depicted the undesirable zone with value of 0 and red zone depict the ideal condition with 100% desirability. Base on welding condition and variables range, optimal desirability zone is 77% for the given values of welding parameters.

7. Validation, Discussion, and Conclusion

After getting the optimal values for factors next stage was to validate these values. In order to do this final weld, the run was conducted by using these optimal values obtained during these analyses. Welding was performed under same circumstances using the same material. Final results were obtained and found very close to the optimal responses as mentioned in Table 11.

Table 11. Comparison between optimized and actual results.

Optimized Factors	Optimized Responses	Actual Results (Responses)
Welding Voltage = 33.2 V	Depth of Penetration = 5.2921 mm	Depth of Penetration = 5.3 mm
Wire Feed Speed = 3. mm	Deposition Efficiency =87.8 %	Deposition Efficiency = 90 %
Welding Speed = 60 cm/ mm	Bead Width = 7.72 mm	Bead Width = 6.52 mm
	Reinforcement = 2.86 mm	Reinforcement = 2.2 mm

This study discloses the application of RSM Box-Behnken design and desirability analyses for gas metal arc welding to optimize the welding output. By using these methodologies optimal values for selected controllable factors and responses are found and then optimal responses values are validated by performing an actual run of the weld and then comparing the actual results with the calculated optimal values. Hence conclusion can be made that for given certain material and similar welding circumstances these analyses can be used for the best quality weld.

Acknowledgements

The completion of this research work could not be possible without support and assistance of so many people whose names may not all be enumerated, however, we would like to express our thanks to particular Mr. Ali Raza lone - QC manager of Saudi Arkad, Mr. Azhar - Ph.D. student of King Fahd University of Petroleum and Minerals (KFUPM), Mr. Saravanan - JGC Department Manager of Construction and the most Mr. ITO Kenji - Senior Manager JGC for their endless support during my research work. The research work's Abstract of same methodology on Flux-cored arc welding (FCAW) was also presented in 15th Annual Congress on Materials Research & Technology [13].

Competing Interests

The authors declare no competing interest.