A comparative analysis of the travelling salesman problem: Exact and machine learning techniques

1. Introduction

The Traveling Salesman Problem (TSP) is one of the variant of Vehicle Routing Problem (VRP) which is a classical and widely studied problem in combinatorial optimization [1]. TSP has been studied in Operations Research (OR), engineering and computer science since \(1950s\) and several techniques been developed to solve this kind of problem [2]. TSP describes a salesman who must travel through \(n\) cities. The order of visiting the cities is not of importance, as long as the salesman visit every city exactly once and return to the starting city [3]. The cities are connected to one another through a weighted link.

In graph theory, TSP can be understood as to searching for the shortest possible Hamiltonian cycle in a graph, in which nodes of the graph represents cities location and edges represents a path from one city to another [3]. Finding optimal solution for TSP is NP-hard, even in 2D case [4]. TSP can be represented as a graph, where the nodes of the graph represents cities and the edges or arcs represent direct routes between the nodes. The goal is to find the path with the least accumulated weights.

In real life scenario, one can expect quick and near optimal solutions rather than the optimal one. As a result, depending on the size of the problem, heuristics or machine learning methods may be used to find optimum or near optimum solutions. Geldenhuys in [5], implemented the branch-and-cut algorithm to solve a large scale TSP where the problem has to be solved several times using \textit{branch-and-cut} algorithm before a solution to the TSP was obtained. Using large-size instances of the TSP, a substantial portion of the computation time of the entire branch and cut algorithm is spent in linear program optimizer. In their work, they constructed a full implementation of branch and cut algorithm, utilizing the special structure, however, did not implement all of the refinements [6], and used some classes of TSP constraints such as Sub-tour elimination, 2-Matching, Comb and Clique-tree inequalities. Their result were compared with that of [7] and realized that the previous outperform theirs, also, realized how important it is to have more classes of constraints which are essential for solving large instances of the TSP. Only implemented a subtour elimination constraints which has less accuracy in terms of solution as compared to the previous studies and adding more classes such as the ones mentioned above will improved the performance of the [7].

TSP can be classified into the following categories:

• (i) Symmetric Traveling Salesman Problem (s-TSP): Let \(V ={v_1 , ... , v_n }\) be a set of cities, \(A={( p , q ) : p , q \in V }\) be the set of edges, and \(d_{pq} =d_{qp}\) be a cost measure associated with the edge \((p, q) \in A\) which is symmetric. The s-TSP is the problem of finding then, a minimal length closed tour that visit each city once. In this case cities \(v_i \in V\) are given by their coordinates \((x_i , y_i )\) and \(d_rs\) is the Euclidean distance between \(r\) and \(s\) then we have an Euclidean TSP.
• (ii) Asymmetric Traveling Salesman Problem (a-TSP): From the above definition, if the cost measure \(d_{pq} \neq d_{qp}\) for at least one \(( p , q )\) then the TSP becomes an aTSP.
• (iii) Multiple Traveling Salesman Problem (m-TSP): Given a set of nodes, let there be m salesmen located at a single depot node. The remaining nodes (cities) that are to be visited are intermediate nodes. Then, the mTSP consists of finding tours for all m salesmen, who all start and end at the same deport, such that each intermediate node is visited exactly once and the total cost of visiting all nodes is minimized.

Nazari et al.[8] presented an end-to-end reinforcement learning framework which can be used to solve the VRP. The model was applied on TSP and the approach outperforms google's OR-tools and classical heuristics on medium-sized problem in terms of the solution quality with computational time. Also, [9] considered a similar technique by solving a CVRP with exact and machine learning methods. Similarly, [10] applied branch and cut algorithm on TSP and solve instance upto \(200\) nodes.

Applying neural networks to combinatorial optimization problem has a very successful history, where the majority of research focuses on the TSP [11]. One of the earliest proposals, is the use of Hopfield networks [12] for the TSP. The authors modify the networks energy function to make it equivalent to the TSP objective and use Lagrange multipliers to penalize the violations of the problems constraints. A limitation of this approach is that, its sensitive to hyper-parameters and the parameter initialization as analyzed by [13]. Abdoun and Abouchabaka in [14], investigated some of the machine learning heuristics for solving the (TSP). In their paper, they considered Nearest Neighbor, Genetic Algorithm, Ant Colony Optimization and Q-Learning. Where they considered several well-known TSPLIB instances for comparison purposes. In which the Q-learning capability was improved by modifications with an additional support with 2-opt localization approach. The results they had are encouraging for those instances that have less than 200 cities.

Applications of Vehicle Routing Problem cut across several areas which includes; Courier service [15], real-time delivery of customers demand [16], milk runs dispatching system in real time [17], milk collection problem [18]. This study is aimed at developing a machine learning algorithm used in solving TSP and compare the solution exact method in order to determine the optimal gap . To achieving this, we set the following objectives:

• (i) Develop a mathematical formulation for TSP,
• (ii) Develop a machine learning algorithm for solving TSP,
• (iii) Apply this method on solving large size problem.

Inspired by advancements in sequence-to-sequence learning [19, 20, 21, 22]. Our new contribution differs from proposed neural combinatorial optimization for solving TSP problems in [22]. The previous frame work was improved by adding local search (2-opt) to the algorithm.

Local search is one of the oldest and the intuitive optimization technique which consist in starting from a solution and continue to improve it by performing a typical local perturbations which is call moves. In optimization, 2-opt is one of the simple local search algorithm for solving the traveling salesman problem. The main idea behind this method is to take route that crosses over itself and reorder it so that it does not i.e, it gradually improve an initially given feasible answer (local search) until it reaches a local optimum and there is no more improvements can be made. The improvement are done using what is called ``inversion''. It is an optimized solution for both symmetric and asymmetric instances. In our case, we are more concerned in using it for 2D symmetric TSP problem. the technique is not guaranty to find global optimum solution but instead it returns an answer that is usually said to be 2-optimal and making it heuristic.

The remainder of our paper is broken down as follows. Section 2 first introduces the mathematical model of TSP and algorithms proposed. The various techniques discussed are then applied on TSP in Section 3. A summary of the findings and proposed future research directions are finally given in Section 4.

2. Mathematical formulation and methods

We shall talk about the Mathematical Formulation of TSP, branch-and-cut and the machine learning algorithms.

Nomenclatures

• G(V,E) represent a complete graph G.
• \(V = \{v_1, v_2, \dots, v_n\}\); denotes set of cities.
• E \( = \{(v_{i}, v_{j}), v_0 \le i,j \le m \} \) edges between \(V\).
• \(d_{ij} = c:\) is the nonnegative cost-matrix of distance travel.
• Decision variable is defined as; \( y_{ij} = \begin{cases} 1 \hspace{0.3cm} \text{if edge} \hspace{0.3cm} (i,j) \in \text{E is in tour } \\ 0 \hspace{0.3cm} \text{Otherwise} \end{cases} \)
• \(y^{*}\) is the optimal solution.
• \(\gamma\) is a tour.
• \(\vert \vert . \vert \vert_{2}\) is euclidean norm.
• x represent sequence of cities.
• \(\mathcal{P}(\gamma \vert x)\) is a parameter of stochastic policy
• \(\{d_{e}c_{i}\}\) sequences of latent memory states
• \(\theta\) is parameter of the pointer network.
• L is the expected tour length.
• \(\delta(v)\) edges that meet vertices V.
• \(y(\delta(v))\) sums over all variables
• \(G(ref, q)\) is a glimpse function
• T is the hyperparameters temperature
• C is a hypaparameters that controls the range of the logits

2.1. Mathematical formulation of TSP using ILP

There are several mathematical formulations for TSP [19]. Employing a variety of constraints that enforce the requirements of the problem in order to demonstrate how such a formulation is used in the comparative analysis as follows:

Given a complete graph \(G = (V,E)\) with \(\vert V \vert = n\) and \( \vert E \vert = m = \frac{n(n-1)}{2}\), and nonnegative cost of distance traveled, \( d_{ij}\), containing each vertex exactly once. Introducing binary variable; \( y_{ij}\) for the possible inclusion of any edge \( (i,j) \in E \) in the tour we get the following classical ILP formulation;

Recall in section one, since we can travel from one city to another, the graph is complete. That is to say, there is an link/edge between every pair of nodes. For each edge in the graph, we associate a binary variable as follows $$ y_{ij} = \begin{cases} 1 \hspace{0.3cm} \text{if edge} \hspace{0.3cm} (i,j) \in \text{E is in tour } \\ 0 \hspace{0.3cm} \text{Otherwise} \end{cases} $$ Also since the edges are undirected, it suffices to include only edges with \( i < j \) in the model. Furthermore, since we are minimizing the total distance traveled during the tour, so we calculate \( d_{ij}\) between each pair of nodes \(i\) and \,\(j\). So the total distance travelled is then the sum of all the distances of the edges which are included in the tour as follows.\ Since the tour can only pass through each city exactly once, then each node in the graph should have exactly one incoming and one outgoing edge i.e for every \(i\) node, exactly two of \(y_{ij}\) binary variables should be equal to 2. And we write it as follows, Furthermore, eliminating sub tours that might arise from the above constraint, we add the following constraints; This constraints requre that for each proper(non-empty) subset of the set of cities V, the number of edges between the nodes of S must be at most \(\vert S \vert - 1.\) Therefore, the final integer linear program of our TSP formulation is as follows; \begin{equation*} Min \sum_{{(i,j) \in E }} d_{ij} y_{ij}, \end{equation*} subject to: \begin{equation*} \sum_{j \in V } y_{ij} = 2 \, \, \forall i \in V, \end{equation*} And if the set of cities \(V\) is of size \(n\) , then there are \( 2^{n} -2 \) subset of \(S\) of \(V\), excluding \( S=V \) and \( S = \emptyset\), where Equation (1) defines the objective function, Equation (2) is the degree equation for each vertex, Equation (3) are the sub tour elimination constraints (SEC), which forbid solution consisting of several disconnected tours, and Equation (4) defines the integrality constraints. Also note that some of the SEC are redundant: for the vertex sets \( S \subset V, S \neq \emptyset\), and \( S^{'} = V \backslash S \) we get pairs of SEC both enforcing the connection os \( S\) and \( S^{'} \).

2.1.1. LP relaxation for TSP

The LP Relaxation for TSP can be described as follows:
Given a complete graph \( G = (V,E) \) with edge costs \(c = ( d_{ij}:i,j \in E )\), the relaxations have variables \( x =(y_{ij} :i,j \in E).\) From our model, we had introduced an equation for which each vertex \(v\) that requires the variables corresponding to edges having \(v\) as an end to sum up to \(2\). And these degree equations are as follows: Also since \( \delta(v) \) is the set of edges that meet vertices \(v\), and \( y(\delta(v))\) sums over all variables in this set, the problem becomes, \begin{eqnarray*} Min \hspace{0.2cm}c^{T}y, \end{eqnarray*} subject to: which is called the degree of LP Relaxation, or sometimes the assignment LP, where \(c^{T} \) is the transpose of c-vector. Also given a non-empty proper subset \(S\) of \(V\), the subtours inequality for \(S\) requires that the variables corresponds to edges joining vertices in \(S\) to vertices in \( V-S\) sum to at least 2. The inequality can be written as Therefore, The subtour relaxation of the TSP is, \begin{equation*} \text{Min} c^{T}y, \end{equation*} subject to: \begin{equation*} y(\delta(v)) = 2 \hspace{0.3cm} \text{for all vertices } v \end{equation*} Note that the LP problem has an exponential number of constraints and cannot be solved with an explicit formulation, but as part of the cutting plane method for the TSP. Therefore, the general form of the TSP relaxations is of the form where \( Cy \leq d\) is the system of \(m\) inequalities satisfied by all tours.

2.2. Branch-and-cut method

The branch-and-cut algorithm is a combination of the cutting plane method and the widely known branch-and-bound algorithm. The cutting plane method for the TSP was introduced by [24]. The method solves the linear programming relaxation of a problem iteratively, and adds cuts after each iteration. With each cut, the feasible region of the linear programming relaxation is shrunk without deleting possible solution tours. An inequality that cuts the solution space of the linear programming relaxation, but does not cut any feasible solutions to the original integer programming problem, is called a valid inequality, or facet-defining. The procedure of solving the linear programming relaxation and searching for valid cuts is repeated until a feasible solution for the original problem is obtained. In the branch-and-cut algorithm, the first step is to initialize a linear programming relaxation of the original problem. Initially, a cutting plane procedure is used until no more valid inequalities can be found anymore. The best solution for the original problem and the relaxed problem is stored. Then, the first branching step is taken on a fractional variable, which means this fractional variable is restricted to be either 0 or 1. This yields two new nodes in the so-called branch-and-cut tree. In every node, the new linear programming relaxation of a problem is solved. If the solution of the relaxed problem is higher than the best solution found for the original problem, this means there is no room for improvement in this branch of the tree and the node is pruned, i.e. cut off. Otherwise, the procedure of branching, solving and looking for valid inequalities is repeated. Whenever a better incumbent solution is found, the bounds throughout the tree are updated. The step by step algorithm of the branch-and-cut is summarized in Algorithm 1 below.

It is observed that at some point in the computation, the truncated cutting plane method may not longer be satisfied with the quality of the cutting planes that is obtained i.e in a situation where its doesn't provide any cut, or in general if the amount of increase in LP lower bound is insignificant when compared to the remaining gap to the value of the best known solution to our problem. So therefore, the branch and cut scheme is used for turning the truncated cutting plane method into a full solution procedure for the TSP.

Given a finite subset \(S\) of points in some \({\mathbb{R}}^{n}\), and our problem is to for some cost vector \(c \in {\mathbb{R}}^{n}\). It is trivial to create an initial linear system \(Ay \leq b\) that is satisfied by all points in S, and we assume that \(P = \{y:Ay \leq b \}\) is bounded. And since \(S\) is finite, it is a simple matter to choose a system that meets this requirements. The bounding process here is to solve the the LP relaxations, starting with and in general And in the main step of this algorithm, there are three cases to be considered depending on the LP solution \(y^{*}\).

Case 1.

Suppose the LP bound is less than the value \( u = c^{T}y^{*}\) of the best point \( \bar{y} \in S\) found thus far in search, and suppose the LP solution is not a point in \(S\). Since the LP relaxation did not provide any optimal solution to the subproblem We carry out a branching step to continue the search process. To do this, a vector \( \alpha \in {\mathbb{R}}^{n}\) and scalars \( \beta^{'} \) and \( \beta^{''} \) are selected such that each member of \(S\) satisfies either \( \alpha^{T}y \leq \beta^{'}\) or \( \alpha^{T}y \geq \beta^{''}\). New subproblems are created by imposing the external constraint \(\alpha^{T}y \leq \beta^{'}\) in one subproblem and \(\alpha^{T}y \geq \beta^{''}\) in the other subproblem.

Case 2.

Suppose the LP bound is less than \(u\) and suppose \(y^{*}\) is in fact a point in \(S\). Here we update \(u\) and \(\bar{y}\) by setting \(u = c^{T}y^{*}\) and also \(\bar{y} = y^{*}\).

Case 3.

If the LP relaxation is infeasible or if the optimal value \(y^{*} \ge u\), then the subproblem can be discarded (no better point in \(S\) satisfies the constraints defining the subproblem.) In the branch-and-cut scheme, this process is argumented by applying the truncated cutting plane algorithm to each of the subproblems, rather than simply relying on the LP relaxation that is presented. The algorithm is as follows:

Note that we impose the condition that the separation routine FINDCUTS return cutting planes that are valid for the entire set \(S\) rather than for the subproblem solutions \( \{y:Cy \leq d \cap S \}\). This standard practice makes it possible to share the cutting planes that are found with other subproblems by maintaining a list of them in a cut pool that can be searched as one of the separation routines.

2.3. Machine learning

In the machine learning method, we used a combination of Neural network and reinforcement learning called the Neural Combinatorial optimization which solves combinatorial optimization problems. Based on our approach, we considered the combination of a policy gradient of [23] which is called the RL pre-training which uses a training set to optimize a Recurrent neural network (RNN) that parameterize a stochastic policy over solutions using the expected reward as the objective. When testing, the policy is fixed and one performs inference by a greedy decoding or sampling and using a local search which involves no pre-training and start from a random policy and its iteratively optimizes the RNN parameters on a single test instance using again the expected reward as the reward objective. The goal of neural combinatorial optimization is to train an agent to match an input sequence to its corresponding optimal output sequence.

In reinforcement learning, the idea behind it is, an agent will learn from the environment by interacting with it and receiving rewards for performing actions.

2.3.1. Neural network architecture for TSP

Based on the previous discussion, we will make emphasis on the 2D Euclidean TSP. Given an input graph, which is represented as a set of cities \(m\) in 2D given by \( x = \{y_{i}\}_{i=1}^{m}\) where \(y_{i} \in {\mathbb{R}}^{2}\), we are concerned in finding a permutation of the points \(\gamma\) (called tour), that visits each city exactly once and has the least total tour length. Tour length is defined by permutation \(\gamma\) as where \(\vert\vert . \vert \vert_{2}\) denote the \(\ell_2\) norm. We aim to learn (from the input points) the parameters of stochastic policy \(\mathcal{P}(\gamma \vert x)\) which assigns higher probabilities to short tours and vice-versa. We then use the chain rule, which is used in sequence to sequence problems to factorize the probability of a tour in our neural network architecture as follows; then we use the individual softmax modules for each terms in (15). We use the approach of [20] called the pointer network which then allows the model to effectively point to a specific position in the input sequence rather than predicting an index value from a fixed size vocabulary. We use the pointer architecture in [20] as our policy model to parametrize our neural network architecture \( \mathcal{P}(\gamma \vert x) \).

This pointer network has two recurrent neural network (RNN) modules which are the encoder and decoder, both of which consist of a long short time memory (LSTM) cells.

The encoder network reads input sequence x, one city at a time, and transforms it into sequence of latent memory states \(\{ enc_{i} \}_{i=1} ^{n} \) where \(enc_{i} \in {\mathbb{R}}^{d}\). The input of the encoder network at any time step \(i\) is a d-dimensional embedding of 2D point \( x_i \), which is obtained through a linear transformation of \(x_{i}\) which is shared across all input steps. This decoder network also maintains its latent memory states \(\{dec_{i} \}_{i=1} ^{n}\) where \( deci_{i} \in {\mathbb{R}}^{d}\) and at each of the step \(i\), it uses a pointer mechanism used to produce a distribution over the next city to visit in the tour. And once the next city is selected, it is passed out as the input to the next decoder step. The input of the first decoder step as shown in [20]vinyals2015pointer} pointer network architecture which is in a d-dimensional vector that is treated as a trainable parameter of our neural network.

The attention function takes the query vector \( q = dec_{i} \in R^{d}\) as input and a set of reference vectors \( ref = \{enc_{1},...,enc_{k}\} \) where \(enc_{i} \in {\mathbb{R}}^{d}\), and it predicts a distribution \( A(ref, q) \) over the set of \(k\) references. And this probability distribution represent the degree to which the model is pointing to reference \(r_{i}\) upon seeing a query \(q\) [22].

2.4. Optimization with policy gradients

We use a supervised loss function comprising of the conditional log-likelihood of [20] which factors into cross entropy objective between the networks output probabilities and the targets provided by a TSP solver. For NP-hard problems, its undesirable to learn from examples because,

• The performance of the model is tied to the quality of the supervised labels.
• Getting high quality labelled data is expensive and may be infeasible for new problem statements.
• One cares about finding a competitive solution more than replicating the results of another algorithm.

By contrast it is believe that reinforcement learning (RL) provides an appropriate paradigm for training neural networks for combinatorial optimization, because these problems have relatively simple reward mechanisms that could be even used at test time. Hence, we proposed to use model free policy based reinforcement learning to optimize the parameters of the pointer network denoted \(\theta\). Our training objective is the expected tour length which given an input graph \(s\), is defined as The graphs are drawn from a distribution \(S\), and the total training objectives involves sampling from the distribution of graphs i.e \( J(\theta) = \mathbb{E}_{x \sim X} L(\gamma \vert x)\). We choose to use the policy gradient methods and stochastic gradient decent to optimize the parameters. We then use the well known REINFORCE algorithm of [23] to formulate the gradient of Equation (16): where \(b(x)\) denotes a baseline function that does not depends on \( \gamma\) and estimates the expected tour length to reduce the variance of the gradients. By drawing \(B\) i.i.d. sample graphs \( x_{1},x_{2},..., x_{B} \sim X \) and sampling a single tour paragraph, i.e \( \gamma \sim \mathcal{P}_{\theta(. \vert x_{j})} \), the gradient in Equation (17) is approximated with Monte Carlo sampling as follows: We then use the exponential moving average of the regards obtained by the network as a choice of the baseline over time to account for the fact that the policy improves with training . Using a parametric baseline to estimate the expected tour length \( \mathbb{E}_{\gamma \sim \mathcal{P} \theta (.\vert x)} L(\gamma \vert x) \) typically improves learning. We therefore, introduce an auxiliary network, called a critic and parameterized it by \( \theta_{v}\), which is to learn the expected tour length found by our current policy \( \mathcal{P}\theta \) given an input sequence X. The critic is trained with stochastic gradient decent on a mean squared error objective between its predictions \( b\theta_{v}(x)\) and the actual tour lengths sampled by the most recent policy. These additional objective function for optimizing the baseline parameters denoted \(\theta_{v}\) is formulated as The train algorithm is as follows:

We perform our updates asynchronously across multiple workers, but each worker also handles a mini-batch of groups for better gradient estimate [22].

2.5. Search strategy

Since evaluating a tour length is not expensive, then out TSP agent can easily simulate a search procedure at inference time by considering multiple candidate solutions per graph and selecting the best which resembles how solvers search over large set of feasible solutions. We consider mainly two search strategies, which are as follows.

2.6. Sampling

We sample multiple candidate tours from our stochastic policy and select the shortest one. We do not actually enforce our model as compare to heuristics solvers to sample different tours during the process. However, the diversity of sampled tour can be controlled with temperature hyperparameters when sampling from our non-parametric sofmax as below.

2.7. Local search (2-opt)

Local search is one of the oldest and the most intuitive optimization technique which consist in starting from a solution and continue to improve it by performing a typical local perturbations which is call moves. In optimization, 2-opt is one of the simple local search algorithm for solving the travelling salesman problem. The main idea behind this method is to take route that crosses over itself and reorder it so that it does not i.e, it gradually improve an initially given feasible answer (local search) until it reaches a local optimum and there is no more improvements can be made. The improvement are done using what is called ``inversion''. It is an optimized solution for both symmetric and asymmetric instances. In our case, we are more concerned in using it for 2D symmetric TSP problem. the technique is not guaranty to find global optimum answer but instead it returns an answer that is usually said to be 2 - optimal and making it heuristic.

2.8. Local search (2-opt) algorithm

• We fine a trial solution \( x \in X \), for which \(M(x)\) is as small as we can make it at a first try.
• We than apply some inversions(transformation), which transforms this trial solutions into some other elements of \(X\), whose measures are progressively smaller.
• Check C for element which might be included in the final \(x\) at an advantage. if there are any such elements try to find a transformation which decreases the measure of the sequence.

Its noted that during training of RL , supervision is not required. Although, it still requires training data and hence generalization depends on the train data distribution. Since the set of cities are encoded, we randomly shuffle the input sequence before feeding it to our pointer network. Which increases the stochasticity of sampling procedure and it leads to large improvements in active search.

3. Results and discussion

The results obtained by applying the exact and machine learning method in solving the 2D symmetric TSP problem will be presented. Several TSPLIB instances was used in testing our solutions and compared with solution found in other literatures. This enable us to provide comparison between optimal solutions and the obtained results. The following instance was considered; Wi29, DJ38, Berlin52, Pr76, KroA100, pr136, pr144, ch150, qa19 and KroA200 from (TSPLIB 1) and (TSPLIB 2) as part of the exact method experiments. Also, for the Heuristic method, we employed the Google Or-tool algorithm in solving the TSP problem. The distance matrix is computed using Euclidean distance. The distance between two points is the length of the path connecting them. The shortest path distance is a straight line in a 2D plane, that is the distance between points \((x_{1}, y_{1}) \, \text{and} \, (x_{2}, y_{2})\) is given by the Euclidean; For the Gap or Error column, we use the below percentage error formula,

3.1. Exact method with TSP

This section presents the performance tests of branch and cut algorithm on Euclidean instances of TSPLIB library. The tests were performed on a computer processor Intel(R) core (TM) i5-2450m cpu 2.60GHZ @ 2.60GHT and 8GB of Ram. The adaptation of the proposed algorithm is coded into a python programming language version \(3.6 \) . Result obtained by applying the exact method in solving the symmetric TSP problem is summarized in the tables below.

Table 1. Exact method.

Instances	Number of Instance	Best Known Solution	Exact Method	Time(sec)	Error(%)
Wi29	29	27603	27603	0.10	0.0
DJ38	38	6656	6656	0.12	0.0
Berlin52	52	7542	7542	0.15	0.0
pr76	76	21282	21282	0.66	0.0
KroA100	100	108159	108159	0.62	0.0
pr136	136	96772	96772	0.44	0.0
pr144	144	58537	58537	1.63	0.0
ch150	150	6528	6528	7.44	0.0
qa194	194	9352	9352	1.83	0.0
KroA200	200	29437	29437	1.61	0.0

Table 1 above shows the results obtained when Exact method was applied on TSP instance. The method give optimality. Similarly, the Table 2 shows the comparison between the exact and google's tool. The exact outperformed the google OR tool. Tables 1 and 2 shows a summary of the results obtained when we applied our exact method algorithm on the TSPLIB instances. From Table 1, the columns in bold are the optimal values and the gap between our method and the optimal value respectively. We can see that the \(6^{th} \) column has errors equal to zero which shows that our exact method has converged to it optimal solution and has no gap with the global optimum. Also, from the \(5^{th}\) column we can conclude that as the number of instances increases, the computational time of our exact methods tends to increase with an exception of the \(8^{th}\) row. Furthermore, from Table 2, we can see that there is a little gap between our exact method and the heuristic method. Which is much larger in the pr144 instance with \(12.05%\) gap or error. Column five of Table 2 shows the execution time of our exact method based on the TSPLIB instances and we see that the time for execution of an instance increases with increases in the number of instance or cities but with a little drop in pr144 execution time. Also, Column six of Table 2 shows the optimal gap between heuristic and exact method.

Table 2. Exact vs. google's or tools on TSP.

Instances	Number of Instance	Exact Method	google's OR Tools	Time(sec)	Error(%)
Wi29	29	27603	27734	0.02	0.47
DJ38	38	6656	6645	0.03	0.17
Berlin52	52	7542	7924	0.03	5.06
Pr76	76	21282	21923	0.07	3.01
KroA100	100	108159	110928	0.22	2.56
pr136	136	96772	101641	0.44	5.03
pr144	144	58537	65592	0.50	12.05
ch150	150	6528	6638	0.42	1.69
qa194	194	9352	9966	0.99	6.57
KroA200	200	29437	31014	1.07	5.36

Figures 1 is the optimal tours for two instances, Figure 1a with \(194\) nodes and Figure 1b with \(200\) nodes.

3.2. Machine learning method on TSP

We have conducted some experiment to investigate the behaviour of our machine learning method(Combination of Neural Network and reinforcement learning in combinatorial optimization) in solving TSP. Five(5) benchmark tasks where considered(Euclidean TSP5,10,20,50,100) data point where drawn from a uniform random distribution in the unit of square \([0,1]\times [0,1] \).

In all the experiment, mini-batched of 128 sequences where used and 128 hidden layers of LSTM cells and the two coordinate of each point were embedded also in a 128-dimensional space. We used ADAM optimization with a learning rate of \(0.001\) for all the dataset which decay in every 5000 step by factor of \(0.96\). Also, for the RL, a training set of mini-batches was generated and the model parameter was updated using the Actor Critic Algorithm \ref{a2} with a test instance. We sampled \(200\) batches of the solutions from the pretrained model.

The model was finally allowed to train much longer since it start from scratch. For each test graph, we run a local search(2-opt) for \(100\) training steps on TSP\(5,10,20,50 \, \, \text{and} \,100.\) The summary of the whole process is as follows:

Table 3 shows a summary of the results obtained after applying our machine learning method. In Table 3, the Task column shows or indicates the TSPLIB instances we have considered in our research and its contained the number of cities to be visited along side with the problem name. The second column shows the optimal solutions known for the TSP instance based on [20]. Column \(3, 4\) represent the best result obtained by using the meta heuristics and Neural combinatorial optimization with reinforcement learning and the percentage gap between the optimal solution and our method respectively. It is observed that that our method performs better than that of [20] for instance less than or equal \(10\)(column 3 with bold numbers) with percentage error or gap of \(1.89\) and \(0.35\) for TSP5 and TSP10 respectively.

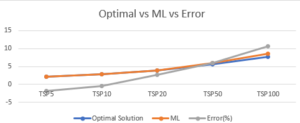
The last column shows that, the model performs relatively very well even though the model wasn't trained directly on the same instance size as in [22]. The solution plot for Optimal, ML and error features in Table 3 is shown in Figure 2. Table 3 shows the execution time in seconds of the machine learning algorithm. As the number of instances increases, the execution time increase. However, the execution time may vary depending on the number of iterations specified in the algorithm and the specification of the device used.

Table 3. Average tour length of our method(ML) and best known result from [20].

Task	Best known solution}}	ML result	ML time	Error(%)	Training(TSP)
TSP5	2.12	2.08	21.78	1.89	5, 10, 50 and 100
TSP10	2.87	2.86	25.15	0.35	10
TSP20	3.83	3.93	42.65	2.61	10 and 100
TSP50	5.68	6.02	155.65	5.99	20
TSP100	7.77	8.60	203.01	10.68	100

From Figure 2 we can see that the gap appears to be negative for instances less than \(12\) and at a point it becomes zero which shows that our model performs better for small instances and as the number of instances increases, the gap also increases.

• The result above shows that as the number of cities increases, the number of iterations required increases sharply, And the increase is not linear increase
• The algorithm developed is non-deterministic,thus it does not promise an optimal solution every time. Although, if it does give near optimal solution in most of the cases, it may fail to converge and give a correct solution.
• This neural network approach is very fast compared to standard programming techniques used for TSP solutions.

3.3. Machine learning and exact method

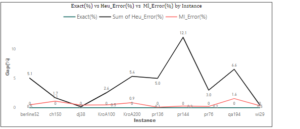
Using the same instances as that of Table 1 on our machine learning algorithm gives the following result as compared to our exact method. The Table 4, column 3 and 4 represent the minimum tour length for each of the instances in column 1 for the exact and machine learning method. The Error column gives the gap between our exact and machine learning method and we can see that the gap is actually very small \((0.22 - 1.56)\) which is negligible in real life application as compared to that of Heuristics.

Figure 3 shows the plot of our exact, machine learning and google's OR tools. We can see from the plot that, the Gap between the Heuristic and our Exact method is very wide as compare to the gap between our Machine learning method. Also, looking further into the exact and machine learning, we can see that the gap is negligible and it overlaps at some point in the plot.

Table 4. Exact method vs. machine learning.

Instances	Number of Instance	Exact	Machine Learning	Error(%)
Wi29	29	27603	27698	0.34
DJ38	38	6656	6685	0.44
Berlin52	52	7542	7579	0.50
pr76	76	21282	21328	0.22
KroA100	100	108159	108673	0.48
pr136	136	96772	96856	0.09
pr144	144	58537	58697	0.27
ch150	150	6528	6601	1.12
qa194	194	9352	9498	1.56
KroA200	200	29437	29687	0.85

Figure 4 is a sample output of 6 plot based on the 100 iterations for the prediction of a TSP with 50 instances trained with 50.

Figures 5 and 6 shows the plot of predicting the permutation of 50 cities at every iteration (10, 20, 30, 50, 80) including the reward before our heuristic search and the reward after our heuristic search.

4. Conclusion

In this paper, we have investigated some solution methods of solving TSP. Where our concentration was based on the Branch and Cut (Exact Method) and machine learning method 2-opt ( Heuristics algorithm). Machine learning itself involves several heuristics algorithm choice which is used for solving combinatorial optimization problems. We compared our solution with optimal solution of TSPLIB instances found previously in other researchers. The branch-and-cut algorithm gave an optimal solution and the machine learning give a near-optimal solution with optimal gap less than \(1%.\) This improved algorithm was able to solve TSP instance upto 200 nodes, it can be used when fast and near-optimal solution is required. In terms of optimal route, this machine learning method can be used in order to obtain a near-optimal solution on a large-sized problem with little experimental time compared with branch-and-cut and Google's tool. Our future work might consider multiple Traveling Salesman Problem with time windows \([a_i, b_i]\). In this problem, each vehicle must visit its defined location within a particular period, and a vehicle may arrive before \(a_i\) and wait till time \(a_i\). The vehicle is not allowed to arrive after \(b_i\).

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

The authors declare no conflict of interest.