A fuzzy solution of nonlinear partial differential equations

1. Introduction

The fuzzy sets were introduced for the first time by Zadeh in [1]. Hundreds of examples have been supplied where the nature of uncertainty in the behavior of given system processes is fuzzy rather than stochastic nature. Recently, many authors showed interest in the study of the theoretical framework of fuzzy initial value problems. Chang and Zadeh [2] introduced the concept of fuzzy derivative. Dubosi and Prade [3] presented the extension principle. The differential and integral calculus for fuzzy-set-valued functions, shortly fuzzy-valued functions was developed in resent work, see [4,5,6,7,8,9].

It is known that phenomena of nature or physical systems can be modeled using partial differential equations (PDEs) such as wave equations, heat equations, Poisson's equation and so on. Hence, studies of PDEs become one of the main topics of modern mathematical analysis and attracted much attention. Many authors developed different methods for solving different kinds of PDEs, see [10,11,12,13,14,15,16,17].

The differential transform method (DTM) was introduced by Zhou [18] and he applied it to solve initial value problems for electric circuit analysis. The DTM is based on Taylor,s series expansion and can be applied to solve both linear and nonlinear ordinary differential equations as well as PDEs. Keskin and Oturanc [19] proposed the RDTM, defining a set of transformation rules to overcome the complicated complex calculations of traditional DTM. Recently some researchers used RDTM for solving different equations, see [20,21,22,23,24,25,26].

This paper is structured as follows: In Section 2, we call some definition on a fuzzy number, fuzzy-valued function and strongly generalized Hukuhara differentiability. In Section 3, Taylor's formula, one-dimensional DTM, and two-and three-dimensional RDTM is introduced. In Section 4, we provide some examples to show the efficiency and simplicity of RDTM. Finally, Section 5 consists of some brief conclusions.

2. Basic concepts

The fuzzy set \(\tilde{u}\in E^{1}\) is called a fuzzy number if \(\tilde{u}\) is a normal, convex fuzzy set, upper semi-continuous and supp\(u=\{x\in R|u(x)>0\}\) is compact. Here \(\overline{A}\) denotes the closure of \(A.\) We use \(E^{1}\) to denote the fuzzy number space [27,28].

For \(\tilde{u},\tilde{v}\in E^{1}\), \(k\in R\), the addition and scalar multiplication are defined by

\begin{align} [\tilde{u}+\tilde{v}]_{r}&=[\tilde{u}]_{r}+[\tilde{v}]_{r},\nonumber\\ [k\tilde{u}]_{r}&=k[\tilde{u}]_{r},\nonumber \end{align} respectively, where \([\tilde{u}]_{r}=\{x:u(x)\geq r\}=[\underline{u}_{r},\overline{u}_{r}]\) for any \(r\in[0,1]\).

We use the Hausdorff distance between fuzzy numbers [28] \(D:E^{1}\times E^{1}\rightarrow[0,+\infty)\) defined by

\begin{align} D(\tilde{u}+\tilde{v})&=\sup_{r\in[0,1]}d([\tilde{u}]_{r}[\tilde{v}]_{r})\nonumber\\ &=\sup_{r\in[0,1]}\max\{|\underline{u}_{r}-\underline{v}_{r}|,|\overline{u}_{r} -\overline{v}_{r}|\},\nonumber \end{align} where \(d\) is the Hausdorff metric. \(D(\tilde{u},\tilde{v})\) is called the distance between \(\tilde{u}\) and \(\tilde{v}\).

Definition 1. [29,30] Let \(\tilde{u}\) be a fuzzy number defined in \({F(R)}\). The \(r\)-level set of \(\tilde{u}\), for any \(r\in[0,1]\) denoted by \(\tilde{u}_{r}\) is a crisp set that contains all elements in \(R\), such that the membership value of \(\tilde{u}\) is greater or equal to \(r\), that is \[ \tilde{u}_{r}=\{{x\in R|\tilde{u}(x)\geq r}\}. \] Whenever we represent the fuzzy number with \(r\)-level set, we mean that it is closed and bounded and it is denoted by \([\underline{u}_{r},\overline{u}_{r}]\), where they represent the lower and upper bound \(r\)-level set of a fuzzy number.

The researchers [31,32] defined the parametrical representation of the fuzzy numbers as in the following definition:

Definition 2. [33] A fuzzy number \(\tilde{u}\) in parametric form is a pair \([\underline{u}_{r},\overline{u}_{r}]\) of functions \(\underline{u}_{r}\) and \(\overline{u}_{r}\) for any \(r\in[0,1]\), which satisfies the following requirements

• \(\underline{u}_{r}\) is a bounded non-decreasing left continuous function in (0,1];
• \(\overline{u}_{r}\) is a bounded non-increasing left continuous function in (0,1];
• \(\underline{u}_{r}\leq\overline{u}_{r}.\)

Some researchers classified the fuzzy numbers into several types of the fuzzy membership function and the triangular fuzzy membership function or also often referred to as triangular fuzzy number is the most widely used membership function.

In order to avoid the inconvenience, in the whole paper, the fuzzy numbers and fuzzy-valued functions are represented with a tilde sign at the top, while the real-value function and interval-valued functions are written directly.

Definition 3. [34] A fuzzy valued function \(\tilde{f}\) of two variable is a rule that assigns to each ordered pair of real numbers, \((x,t)\), in a set \(D\), a unique fuzzy number denoted by \(\tilde{f}(x,t)\). The set \(D\) is the domain of \(\tilde{f}\) and its range is the set of values taken by \(\tilde{f}\), i.e., \(\{\tilde{f}(x,t)|(x,t)\in D\}\).

The parametric representation of the fuzzy valued function \(f:D\rightarrow E^{1}\) is expressed by \(\tilde{f}(x,t;r)=[\underline{f}(x,t;r),\overline{f}(x,t;r)]\), for all \((x,t)\in D\) and \(\alpha\in[0,1]\).

Definition 4. [34,35] A fuzzy valued function \(f:D\rightarrow E^{1}\) is said to be fuzzy continuous at \((x_{0},t_{0})\in D\) if \(\lim_{(x,t)\rightarrow(x_{0},t_{0})}\tilde{f}(x,t)=f(x_{0},t_{0})\). We say that \(\tilde{f}\) is fuzzy continuous on \(D\) if \(\tilde{f}\) is fuzzy continuous at every point \((x_{0},t_{0})\) in \(D\).

Definition 5. [36,37] The generalized Hukuhara difference of two fuzzy numbers \(\tilde{u},\tilde{v}\in E^{1}\) is defined as follows:

In terms of the \(r-\)levels, we get \([\tilde{u}\ominus_{gH}\tilde{v}]=[\min\{\underline{u}_{r}- \underline{v}_{r},\overline{u}_{r}-\overline{v}_{r}\},\max\{\underline{u}_{r} -\underline{v}_{r},\overline{u}_{r}-\overline{v}_{r}\}]\) and if the H-difference exists, then \(\tilde{u}\ominus\tilde{v}=\tilde{u}\ominus_{gH}\tilde{v}\); the conditions for existence of \(\tilde{w}=\tilde{u}\ominus_{gH}\tilde{v}\in E^{1}\) are It is easy to show that (i) and (ii) are both valid if and only if \(\tilde{w}\) is a crisp number. In this case, it is possible that the gH-difference of two fuzzy numbers does not exist. To address this shortcoming, a new difference of fuzzy numbers was presented in [37]

Definition 6. [38] Let \(\tilde{u}(x,t): D\rightarrow E^{1}\) and \((x_{0},t)\in D\). We say that \(\tilde{u}\) is strongly generalized Hukuhara differentiable on \((x_{0},t)\) (gH-differentiable for short) if there exists an element \(\frac{\partial \tilde{u}}{\partial x}|_{(x_{0},t)}\in E^{1}\) such that

• (i)   for all \(h>0\) sufficiently small, \(\exists\; \tilde{u}(x_{0}+h,t)\ominus_{gH} \tilde{u}(x_{0},t), \tilde{u}(x_{0},t) \ominus_{gH} \tilde{u}(x_{0}-h,t)\) and the limits (in the metric D) \begin{equation} \lim_{h\rightarrow0+}\frac{\tilde{u}(x_{0}+h,t)\ominus_{gH} \tilde{u}(x_{0},t)}{h}=\lim_{h\rightarrow0+}=\frac{ \tilde{u}(x_{0},t) \ominus_{gH} \tilde{u}(x_{0}-h,t)}{h}=\left.\frac{\partial \tilde{u}}{\partial x}_{_{gH}}\right|_{(x_{0},t)},\nonumber \end{equation} or
•   (ii) for all \(h>0\) sufficiently small, \(\exists\; \tilde{u}(x_{0},t) \ominus_{gH} \tilde{u}(x_{0}+h,t), \tilde{u}(x_{0}-h,t)\ominus_{gH} \tilde{u}(x_{0},t)\) and the limits \begin{equation} \lim_{h\rightarrow0+}\frac{\tilde{u}(x_{0},t)\ominus_{gH} \tilde{u}(x_{0}+h,t)}{-h} =\lim_{h\rightarrow0+}\frac{\tilde{u}(x_{0}-h,t)\ominus_{gH} \tilde{u}(x_{0},t)}{-h}=\left.\frac{\partial \tilde{u}}{\partial x}_{gH}\right|_{(x_{0},t)},\nonumber \end{equation} or
• (iii)   for all \(h>0\) sufficiently small, \(\exists\; \tilde{u}(x_{0}+h,t)\ominus_{gH} \tilde{u}(x_{0},t), \tilde{u}(x_{0}-h,t)\ominus_{gH} \tilde{u}(x_{0},t)\) and the limits \begin{equation} \lim_{h\rightarrow0+}\frac{\tilde{u}(x_{0}+h,t)\ominus_{gH} \tilde{u}(x_{0},t)}{h}=\lim_{h\rightarrow0+}\frac{\tilde{u}(x_{0}-h,t)\ominus_{gH} \tilde{u}(x_{0},t)}{-h}=\left.\frac{\partial \tilde{u}}{\partial x}_{gH}\right|_{(x_{0},t)},\nonumber \end{equation} or
• (iv)   for all \(h>0\) sufficiently small, \(\exists\; \tilde{u}(x_{0},t) \ominus_{gH} \tilde{u}(x_{0}+h,t), \tilde{u}(x_{0},t) \ominus_{gH} \tilde{u}(x_{0}-h,t)\) and the limits \begin{equation} \lim_{h\rightarrow0+}\frac{\tilde{u}(x_{0},t)\ominus_{gH} \tilde{u}(x_{0}+h,t)}{-h}=\lim_{h\rightarrow0+}\frac{ \tilde{u}(x_{0},t) \ominus_{gH} \tilde{u}(x_{0}-h,t)}{h}=\left.\frac{\partial \tilde{u}}{\partial x}_{gH}\right|_{(x_{0},t)}.\nonumber \end{equation}

Lemma 1. [39] Let \(\tilde{u}(x,t): D \rightarrow E^1.\) Then the following statements hold:

• (a)   If \(\tilde{u}(x,t)\) is \((i)\)-partial differentiable for \(x\) (i.e., \(\tilde{u}\) is partial differentiable for \(x\) under the meaning of Definition 5 \((i)\), similarly to \(t\)), then
  \begin{equation} \left[\frac{\partial \tilde{u}}{\partial x}\right]_r=\left[\frac{\partial \underline{u}(x,t)(r)}{\partial x}, \frac{\partial \bar{u}(x,t)(r)}{\partial x}\right], \end{equation}

  (4)
• (b)   If \(\tilde{u}(x,t)\) is \((ii)\)-partial differentiable for \(x\) (i.e., \(\tilde{u}\) is partial differentiable for \(x\) under the meaning of Definition 5 \((ii)\), similarly to \(t\)), then
  \begin{equation} \left[\frac{\partial \tilde{u}}{\partial x}\right]_r=\left[\frac{\partial \bar{u}(x,t)(r)}{\partial x}, \frac{\partial \underline{u}(x,t)(r)}{\partial x}\right]. \end{equation}

  (5)

Remark 1. For \(\tilde{u}(x,t): D \rightarrow E^1,\) the following results hold:

if \((i,i), (ii,ii)\)-\(\frac{\partial^{2} \tilde{u}}{\partial x^{2}}\) exist, and if \((i,ii), (ii,i)\)-\(\frac{\partial^{2}\tilde{u}}{\partial t^{2}}\) exist.

3. Analysis of the method

In this section, we shall give some definitions and theorems of the Taylor series, one-dimensional DTM, and two-and three-dimensional RDTM.

Definition 7. [40] A Taylor series for the polynomial of degree \(n\) is defined as

Theorem 1. If the function \(f(x)\) has \((n+1)\) derivatives on an interval \((c-r,c+r)\) for some \(r>0\), and \(\lim_{n\rightarrow\infty}R_{n}(x)=0\), for all \(x\in(c-r,c+r)\), where \(R_{n}(x)\) is the error between \(F_{n}(x)\) and the polynomial function \(f(x)\) then the Taylor series expanded about \(x=c\) converges to \(f(x).\) Thus

3.1. Differential transform method

We consider the following one-dimensional DTM:

Definition 8. [26] The differential transform \(F(j)\) of the function \(f(x)\) for \(j^{th}\) order derivative is defined as

Definition 9. [26] The inverse differential transform of \(F(j)\) is defined as

The Equation (9) is the Taylor series expansion of \(f(x)\) at \(x=x_{0}\). From Equations (10) and (11), the following basic operations of DTM can be deduced

•   If \(f(x)=y_{1}(x)\pm y_{2}(x),~~\mbox {then}~~ F(j)=Y_{1}(j)\pm Y_{2}(j).\)
•   If \(f(x)=ay_{1}(x), ~\mbox {then}~~ F(j)=aY_{1}(j), \mbox{where a is a constant}.\)
•   If \(f(x)=\frac{dy_{1}(x)}{dx}~~\mbox {then}~~F(j)=(j+1)Y_{1}(j+1)\).
•   If \(f(x)=\frac{d^{2}y_{1}(x)}{dx^{2}}~~\mbox {then}~~F(j)=(j+1)(j+2)Y_{1}(j+2)\).
•   If \(f(x)=\frac{d^{n}y_{1}(x)}{dx^{n}},~~\mbox {then}~~ F(j)=\frac{(j+1)!}{j!}Y_{1}(j+1).\)
•   If \(f(x)=y_{1}(x)y_{2}(x),~~\mbox {then}~~ F(x)=\sum^{j}_{i=0}Y_{1}(i)Y_{2}(j-i).\)
•   If \(f(x)=x^{n},~~\mbox {then}~~ F(j)=\mu(j-n)~~\mbox where ~\mu(j-n) =\left\{\begin{aligned} &1, ~~~j=n,\\ &0, ~~~j\neq n. \end{aligned}\right.\)
•   If \(f(x)=(1+x)^{n}~~\mbox {then}~~F(j)=\frac{n(n-1)......(n-j+1)}{j!}\).
•   If \(f(x)=e^{a x},~~\mbox {then}~~ F(j)=\frac{a^{j}}{j!},\mbox {where \(a\) is a constants}.\)
•   If \(f(x)=\sin(\omega x+\alpha),\mbox {then}~ F(j)=\frac{\omega^{j}}{j!}\sin(\frac{j\pi}{2}+\alpha),~\mbox{ where \(\omega\) and \(\alpha\) are constants}.\)
•   If \(f(x)=cos(\omega x+\alpha), \mbox {then} F(j)=\frac{\omega^{j}}{j!}\cos(\frac{j\pi}{2}+\alpha),~\mbox{ where \(\omega\) and \(\alpha\) are constants}.\)

3.2. Reduced differential transform method

We consider the following two-dimensional RDTM:

Definition 10. [41] If the function \(w(x,t)\) is analytical and differentiable continuously with respect to time \(t\) and space \(x\) in the domain of interest, then we get

where the t-dimensional spectrum function \(W_{j}(x)\) is the transformed function of \(w(x,t)\). Here the lower case function \(w(x,t)\) represents the original function while the upper case \(W_{j}(x)\) stands for the transformed function.

Definition 11. [41] The inverse differential transform of \(W_{j}(x)\) is defined as

Thus combining (12) and (13), we can express the solution as The basic concept of RDTM mainly comes from the power series expansion. For two-dimensional function

• \(w(x,t)~~~\text{then}~~~W_{j}(x)=\frac{1}{j!}\left[\frac{\partial^{j}}{\partial x^{j} }u(x,t)\right]_{t=0}\).
• \(u(x,t)=w(x,t)\pm v(x,y),~~~\mbox {then}~~~U_{j}(x)=W_{j}(x)\pm V_{j}(x).\)
• \(u(x,t)=\alpha w(x,t),~~~\mbox {then}~~~ U_{j}(x)=\alpha W_{j}(x),\)   where \(\alpha\) a is constant.
• \(u(x,t)=x^{m} t^{n},~~~\mbox {then}~~~ U_{j}(x)=x^{m}\delta(j-n), \mbox{where}   \delta(j-n)= \left\{\begin{aligned} &1~~~~~~~\mbox {for}~~~j=n,\\ &0~~~~~~~\mbox {for}~~j\neq n. \end{aligned}\right.\)
• \(u(x,t)=x^{m} t^{n}w(x,t),~~~\mbox {then}~~~U_{j}(x)=x^{m}W_{j-n}(x)\).
• \(u(x,t)=w(x,t)v(x,t),~~~\mbox {then}~~~ U_{j}(x)=\sum^{j}_{r=0}W_{r}(x)V_{j-r}(x)=\sum^{j}_{r=0}V_{r}(x)W_{j-r}(x)\).
• \(u(x,t)=\frac{\partial^{r}}{\partial t^{r}}w(x,t),~~~\mbox {then}~~~ U_{j}(x)=\frac{(j+r)!}{j!}W_{j+r}(x)\).
• \(u(x,t)=\frac{\partial}{\partial x}w(x,t),~~~\mbox {then}~~~ U_{j}(x)=\frac{\partial}{\partial x}W_{j}(x).\)
• \(u(x,t)=\frac{\partial^{2}}{\partial x^{2}}w(x,t),~~~\mbox {then}~~~ U_{j}(x)=\frac{\partial^{2}}{\partial x^{2}}W_{j}(x).\)

For three-dimensional function

• \(w(x,y,t)~~~ \mbox{then}~~~ W_{j}(x,y)=\frac{1}{j!}\left[\frac{\partial^{j}}{\partial x^{j}}u(x,y,t)\right]_{t=0}\).
• \(u(x,y,t)=w(x,y,t)\pm v(x,y,t)~~~\mbox{then}~~~ U_{j}(x,y)=W_{j}(x,y)\pm V_{j}(x,y)\).
• \(u(x,y,t)=\lambda w(x,y,t)~~~\mbox{then}~~~U_{j}(x,y)=\lambda W_{j}(x,y), \mbox{where \(\lambda\) a is constant}\).
• \(u(x,y,t)=x^{m} y^{n} t^{p}~~~\mbox{then}~~~U_{j}(x)=x^{m} y^{n}\delta(j-p),~~\mbox{where}~~ \delta(j-p)= \left\{\begin{aligned} &1~~~~~~~\mbox {for}~~~j=p,\\ &0~~~~~~~\mbox {for}~~j\neq p. \end{aligned}\right.\)
• \(u(x,y,t)=x^{m} y^{n} t^{p}w(x,y,t)~~~\mbox{then}~~~U_{j}(x,y)=x^{m} y^{n}W_{j-p}(x,y)\).
• \(u(x,y,t)=w(x,y,t)v(x,y,t)~~~\mbox{then}~~~U_{j}(x,y)=\sum^{j}_{r=0}W_{r}(x,y)V_{j-r}(x,y)= \sum^{j}_{r=0}V_{r}(x,y)W_{j-r}(x,y)\).
• \(u(x,y,t)=\frac{\partial^{r}}{\partial t^{r}}w(x,y,t)~~~\mbox{then}~~~ ~U_{j}(x,y)=\frac{(j+r)!}{j!}W_{j+1}(x,y)\).
• \(u(x,y,t)=\frac{\partial}{\partial x}w(x,y,t)~~~\mbox{then}~~~U_{j}(x,y)=\frac{\partial }{\partial x}W_{j}(x,y)\).
• \(u(x,y,t)=\frac{\partial^{2}}{\partial x^{2}}w(x,y,t)~~~\mbox{then}~~~U_{j}(x,y)=\frac{\partial^{2}}{\partial x^{2}}W_{j}(x,y)\).
• \(u(x,y,t)=\frac{\partial^{2}}{\partial y^{2}}w(x,y,t)~~~\mbox{then}~~~U_{j}(x,y)=\frac{\partial^{2}}{\partial y^{2}}W_{j}(x,y)\).

4. Examples

In this section, we demonstrate how RDTM can be easily applied to obtain the exact solutions of the fuzzy partial differential equations.

Example 1. Consider the following one-dimensional initial value problem describing fuzzy heat-like equations

subject to the initial condition where \((n = 1,2,3,\ldots).\) Now \([\underline{\tilde{k}^{n}}](r)=r^{n}\) and \( [\overline{\tilde{k}^{n}}](\alpha)=(2-r)^{n}.\) The parametric form of (15) is for \(r\in [0,1],\) where \(\underline{u}\) stands for \(\underline{u}(x,t;r),\) and \(\overline{u}\) stands for \(\overline{u}(x,t;r).\) Applying the RDTM on Equations (18) and (19), we get the recurrence relation as where \(\tilde{U}_{j}(x;r) = [\underline{U}_{j}(x;r),\overline{U}_{j}(x;r)]\) is the transform function. From the initial condition (16), we get Substituting \(\tilde{U}_{0}(x;r) = [\underline{U}_{0}(x;r), \overline{U}_{0}(x;r)]\) into the recurrence relation (20), we get the following \(\tilde{U}_{j}(x;r)\) values successively \begin{align} \left.\begin{aligned} \underline{U}_{1}(x;r)&=2(x^{2}+5)r^{n}\nonumber\\ \underline{U}_{2}(x;r)&=\frac{2^{2}(x^{2}+5)r^{n}}{2!}\nonumber\\ \overline{U}_{3}(x;r)&=\frac{2^{3}(x^{2}+5)r^{n}}{3!}\nonumber\\ \overline{U}_{4}(x;r)&=\frac{2^{4}(x^{2}+5)r^{n}}{4!}\nonumber\\ \vdots\nonumber \end{aligned}\right\} \end{align} and \begin{align} \left.\begin{aligned} \underline{U}_{1}(x;r)&=2(x^{2}+5)(2-r)^{n}\nonumber\\ \underline{U}_{2}(x;r)&=\frac{2^{2}(x^{2}+5)(2-r)^{n}}{2!}\nonumber\\ \overline{U}_{3}(x;r)&=\frac{2^{3}(x^{2}+5)(2-r)^{n}}{3!}\nonumber\\ \overline{U}_{4}(x;r)&=\frac{2^{4}(x^{2}+5)(2-r)^{n}}{4!}\nonumber\\ \vdots\nonumber \end{aligned}\right\} \end{align} The inverse differential transform of \(\tilde{U}_{j}(x;r)\) is obtained from the relations \begin{align} \underline{u}(x,t;r)&=\sum^{\infty}_{j=0}\underline{U}_{j}(x;r)t^{j},\nonumber\\ \overline{u}(x,t;r)&=\sum^{\infty}_{j=0}\overline{U}_{j}(x;r)t^{j},\nonumber \end{align} and the exact solution is \begin{align} \tilde{u}(x,t;r)&=\left[r^{n},(2-r)^{n}\right]\odot\left((x^{2}+5)e^{2t}+x-5\right), \;\;\;\; 0\leq r\leq1.\nonumber \end{align}

Example 2. Consider the following two-dimensional initial value problem describing fuzzy heat-like equations

subject to the initial condition where \((n = 1,2,3,\ldots).\) Now \([\underline{\tilde{k}^{n}}](r)=(0.2+0.2r)^{n}\) and \([\overline{\tilde{k}^{n}}](\alpha)=(0.6-0.2r)^{n}.\) The parametric form of (23) is for \(r\in [0,1],\) where \(\underline{u}\) stands for \(\underline{u}(x,t)(r)\) and \(\overline{u}\) stands for \(\overline{u}(x,t)(r),.\) Applying the RDTM on Equations (26) and (27), we get the recurrence relation as where \(\tilde{U}_{j}(x,y;r)\) is the transform function. From the initial condition (24), we get \begin{align*} \underline{U}_{0}(x,y;r)&=(0.2+0.2r)^{n}+(x^{2}+y^{2}),\\ \overline{U}_{0}(x,y;r) &=(0.6-0.2r)^{n}+(x^{2}+y^{2}). \end{align*} Substituting \(\tilde{U}_{0}(x,y;r)\) into the recurrence relation (28), we get the following \(\tilde{U}_{j}(x,y;r)\) values successively \begin{align} \left.\begin{aligned} \underline{U}_{1}(x,y;r)&=(0.2+0.2r)^{n}+(x^{2}+y^{2})\nonumber\\ \underline{U}_{2}(x,y;r)&=\frac{(0.2+0.2r)^{n}+(x^{2}+y^{2})}{2!}\nonumber\\ \underline{U}_{3}(x,y;r)&=\frac{(0.2+0.2r)^{n}+(x^{2}+y^{2})}{3!}\nonumber\\ \underline{U}_{4}(x,y;r)&=\frac{(0.2+0.2r)^{n}+(x^{2}+y^{2})}{4!}\nonumber\\ \vdots\nonumber \end{aligned}\right\} \end{align} and \begin{align} \left.\begin{aligned} \overline{U}_{1}(x,y;r)&=(0.6-0.2r)^{n}+(x^{2}+y^{2})\nonumber\\ \overline{U}_{2}(x,y;r)&=\frac{(0.6-0.2r)^{n}+(x^{2}+y^{2})}{2!}\nonumber\\ \overline{U}_{3}(x,y;r)&=\frac{(0.6-0.2r)^{n}+(x^{2}+y^{2})}{3!}\nonumber\\ \overline{U}_{4}(x,y;r)&=\frac{(0.6-0.2r)^{n}+(x^{2}+y^{2})}{4!}\nonumber\\ \vdots\nonumber \end{aligned}\right\} \end{align} The solution for \(\tilde{u}(x,t;r)\) is \begin{align} \underline{u}(x,y,t;r)&=\sum^{\infty}_{j=0}\underline{U}_{j}(x,y;r)t^{j}=(0.2+0.2r)^{n}+\left[(x^{2}+y^{2})\left(1+t+\frac{t^{2}}{2!}+\frac{t^{3}}{3!} +\frac{t^{4}}{4!}+\cdot\cdot\cdot\infty\right)\right],\nonumber\\ \overline{u}(x,y,t;r)&=\sum^{\infty}_{j=0}\overline{U}_{j}(x,y;r)t^{j}=(0.6-0.2r)^{n}+\left[(x^{2}+y^{2})\left(1+t+\frac{t^{2}}{2!}+\frac{t^{3}}{3!} +\frac{t^{4}}{4!}+\cdot\cdot\cdot\infty\right)\right],\nonumber \end{align} and the exact solution is \begin{align} \tilde{u}(x,y,t;r)=\left[(0.2+0.2r)^{n},(0.6-0.2r)^{n}\right]\oplus\left((x^{2}+y^{2})\exp(t)\right), 0\leq r\leq 1.\nonumber \end{align}

Example 3. We consider following two-dimensional initial value problem describing heat-like equations

subject to the initial condition where \begin{align} \label{e4.21} \tilde{\nu}(x,y,t;r) & = (-1,0,1)\odot(xy)^{2}\nonumber\\ & = \left[(r-1)^{n},(1-r)^{n}\right]\odot(xy)^{2}, 0\leq r\leq1, (n = 1,2,3,...), \tilde{0}\in E^{1}.\nonumber \end{align} The parametric form of (29) is \begin{align*} \frac{\partial \underline{u}}{\partial t} &= (r-1)^{n}(xy)^{2}+\frac{1}{4}\left[x^{2}\frac{\partial^{2} \underline{u}}{\partial x^{2}}+ y^{2}\frac{\partial^{2} \underline{u}}{\partial y^{2}}\right], 0< x,y< 1, t>0,\\ \frac{\partial\overline{ u}}{\partial t} &= (1-r)^{n}(xy)^{2}+\frac{1}{4}\left[x^{2}\frac{\partial^{2} \overline{u}}{\partial x^{2}}+ y^{2}\frac{\partial^{2} \overline{u}}{\partial y^{2}}\right], 0< x,y< 1, t>0. \end{align*} Applying the RDTM, we get the recurrence relation as where \(\delta(j) = 1\) when \(j = 0\), and \(\delta(j) = 0\) when \(j\neq0\). Moreover \(\tilde{U}_{j}(x,y;r) = \left[\underline{U}_{j}(x,y;r), \overline{U}_{j}(x,y;r)\right]\) is the transform function. From the initial conditions, we obtain Substituting \(\tilde{U}_{0}(x,y;r)\) into the recurrence relation (31), we get the following \(\tilde{U}_{j}(x,y;r)\) values successively \begin{align} \left.\begin{aligned} \underline{U}_{1}(x,y;r) &= (r-1)^{n}x^{2}y^{2}\\ \underline{U}_{2}(x,y;r) &= \frac{(r-1)^{n}x^{2}y^{2}}{2!}\nonumber\\ \underline{U}_{3}(x,y;r) &= \frac{(r-1)^{n}x^{2}y^{2}}{3!}\\ \underline{U}_{4}(x,y;r) &= \frac{(r-1)^{n}x^{2}y^{2}}{4!}\\ &\vdots \end{aligned}\right\} \end{align} and \begin{align} \left.\begin{aligned} \overline{U}_{1}(x,y;r) &= (1-r)^{n}x^{2}y^{2}\\ \overline{U}_{2}(x,y;r) &= \frac{(1-r)^{n}x^{2}y^{2}}{2!}\nonumber\\ \overline{U}_{3}(x,y;r) &= \frac{(1-r)^{n}x^{2}y^{2}}{3!}\\ \overline{U}_{4}(x,y;r) &= \frac{(1-r)^{n}x^{2}y^{2}}{4!}\\ \vdots \end{aligned}\right\} \end{align} The solution for \(\tilde{u}(x,t;r)\) is \begin{align} \underline{u}(x,y,t;r) &= \sum^{\infty}_{j=0}\underline{U}_{j}(x,y,t;r)t^{j}= (r-1)^{n}\left[(x^{2}y^{2})\left(1+t+\frac{t^{2}}{2!}+\frac{t^{3}}{3!}+\frac{t^{4}}{4!}+...\infty\right)\right], \nonumber\\ \overline{u}(x,y,t;r) &= \sum^{\infty}_{j=0}\overline{U}_{j}(x,y,t;r)t^{j}= (1-r)^{n}\left[(x^{2}y^{2})\left(1+t+\frac{t^{2}}{2!}+\frac{t^{3}}{3!}+\frac{t^{4}}{4!}+...\infty\right)\right], \nonumber \end{align} and the exact solution is \begin{align} \tilde{u}(x,y,t;r) = \left[(r-1)^{n},(1-r)^{n}\right]\odot\left((x^{2}y^{2})\exp(t)\right),\;\;\; 0\leq r\leq 1. \nonumber \end{align}

Example 4. We consider the following fuzzy partial differential equation

subject to the initial condition where (n = 1,2,3,...). Now \([\underline{\tilde{k}^{n}}](r)=(0.5+0.5r)^{n}\) and \([\overline{\tilde{k}^{n}}](\alpha)=(1.5-0.5r)^{n}.\) The parametric form of (34) is for \(r\in [0,1],\) where \(\underline{u}\) stands for \(\underline{u}(x,t)(r)\) and \(\overline{u}\) stands for \(\overline{u}(x,t)(r)\). Applying the RDTM on Equations (37) and (38), we get the recurrence relation as The transformed initial condition (35) becomes For different values of \(j\), we get the following results \begin{align} \left.\begin{aligned} \underline{U}_{1}(x;r)&=(0.5+0.5r)-1\nonumber\\ \underline{U}_{2}(x;r)&=(0.5+0.5r)+1\nonumber\\ \underline{U}_{3}(x;r)&=(0.5+0.5r)-1\nonumber\\ \underline{U}_{4}(x;r)&=(0.5+0.5r)+1\nonumber\\ \vdots\nonumber \end{aligned}\right\} \end{align} and \begin{align} \left.\begin{aligned} \overline{U}_{1}(x;r)&=(1.5-0.5r)-1\nonumber\\ \overline{U}_{2}(x;r)&=(1.5-0.5r)+1\nonumber\\ \overline{U}_{3}(x;r)&=(1.5-0.5r)-1\nonumber\\ \overline{U}_{4}(x;r)&=(1.5-0.5r)+1\nonumber\\ \vdots\nonumber \end{aligned}\right\} \end{align} The solution for \(\tilde{u}(x,t;r)\) is \begin{align} \underline{u}(x,t;r)&=\sum^{\infty}_{j=0}\underline{U}_{j}(x;r)t^{j} = \left(\underline{U}_{0}(x;r)+\underline{U}_{1}(x;r)t+\underline{U}_{2}(x;r)t^{2}+ \underline{U}_{3}(x;r)t^{3}+\cdot\cdot\cdot\right)\nonumber\\ &=(0.5+0.5r)+(1-t+t^{2}-t^{3}+\cdot\cdot\cdot),\nonumber\\ \overline{u}(x,t;r)&=\sum^{\infty}_{j=0}\overline{U}_{j}(x;r)t^{j} = \left(\overline{U}_{0}(x;r)+\overline{U}_{1}(x;r)t+\overline{U}_{2}(x;r)t^{2} +\overline{U}_{3}(x;r)t^{3}+\cdot\cdot\cdot\right)\nonumber\\ &=(1.5-0.5r)+(1-t+t^{2}-t^{3}+\cdot\cdot\cdot),\nonumber \end{align} and the exact solution is \begin{align} \tilde{u}(x,t;r) = \left[(0.5+0.5r)^{n},(1.5-0.5r)^{n}\right]\oplus\left[\frac{1}{1+t}\right],\;\;\; 0\leq r\leq 1.\nonumber \end{align} Figure 1 illustrate that the left-hand functions of the r-level set of \(\tilde{u}\) (u lower) are always increasing functions of \(r\) and the right-hand functions of the r-level set of \(\tilde{u}\) (u upper) are always decreasing functions of \(r\) in the above examples.

5. Conclusion

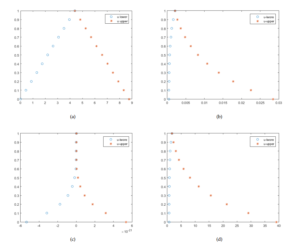
In this paper, the reduced differential transform method (RDTM) has been successfully applied for solving fuzzy nonlinear partial differential equations under gH-differentiability. The solutions are considered as infinite series expansions that converge rapidly to the exact solutions. We solved some examples to illustrate the proposed method. The results reveal that the proposed method is a powerful and efficient technique for solving fuzzy nonlinear partial differential equations.

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest

The authors declare no conflict of interest.