Open Journal of Mathematical Analysis
ISSN: 2616-8111 (Online) 2616-8103 (Print)
DOI: 10.30538/psrp-oma2017.0002
K-Banhatti and K-hyper Banhatti indices of dominating David Derived network
Wei Gao, Batsha Muzaffar\(^{1}\), Waqas Nazeer
School of Information Science and Technology, Yunnan Normal University, Kunming 650500, China.; (W.G)
Department of Mathematics and Statistics, University of Lahore, Lahore-54590, Pakistan.; (B.M)
Division of Science and Technology, University of Education, Lahore-54590, Pakistan.; (W.N)
\(^{1}\)Corresponding Author; batshamuzaffar41@gmail.com
Abstract
Keywords:
Introduction
Chemical graph theory is a branch of graph theory in which a chemical compound is represented by simple graph called molecular graph in which vertices are atoms of compound and edges are the atomic bounds. A graph is connected if there is atleast one connection between its vertices. Throughout this paper we take \(G\) a connected graph. If a graph does not contain any loop or multiple edges then it is called a network. Between two vertices \(u\) and \(v\), the distance is the shortest path between them and is denoted by in graph \(G\). For a vertex \(v\) of \(G\) the degree is number of vertices attached with it. The edge connecting the vertices \(u\) and \(v\) will be denoted by \(uv\). Let \(d_{G}(e)\) denote the degree of an edge \(e\) in \(G\), which is defined by \(d_{G}(e)=d_{G}(u) + d_{G}(v)- 2\) with \(e=uv\). The degree and valence in chemistry are closely related with each other. We refer the book [1] for more details. Now a day another emerging field is Cheminformatics, which helps to predict biological activities with the relationship of Structure-property and quantitative structure-activity. Topological indices and Physico-chemical properties are used in prediction of bioactivity if underlined compounds are used in these studies [2,3 ].
A number that describe the topology of a graph is called topological index. In 1947, the first and most studied topological index was introduced by Weiner [4]. For more details about this index can be found in [5, 6]. In 1975, Milan Randic introduced the Randic index [7]. Bollobas et al. [8] and Amic et al. [9] in 1998, working independently defined the generalized Randic index. This index was studied by both mathematicians and chemists [10]. For details about topological indices, we refer [11,12 ] The first and second \(K\)-Banhatti indices of \(G\) are defined as:
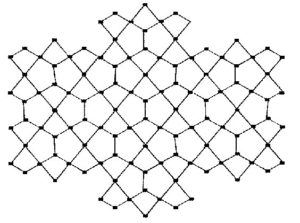
$$B_{1}(G)=\sum\limits_{ue}[d_{G}(u)+d_{G}(e)]$$ and $$B_{2}(G)=\sum\limits_{ue}[d_{G}(u)\times d_{G}(e)]$$ where ue means that the vertex \(u\) and edge e are incident in \(G\). The first and second K-hyper Banhatti indices of G are defined as $$HB_{1}(G)=\sum\limits_{ue}[d_{G}(u)+d_{G}(e)]^{2}$$ and $$HB_{2}(G)=\sum\limits_{ue}[d_{G}(u)\times d_{G}(e)]^{2}.$$ We refer [13] for details about these indices. The David derived and dominating David derived network of dimension \(n\) can be constructed as follows [14]: consider a n dimensional star of David network . Insert a new vertex on each edge and split it into two parts, we will get David derived network \(DD(n)\) of dimension \(n\).Figure 1. Dominating David derived network of the first type \(D_{1}(2)\)
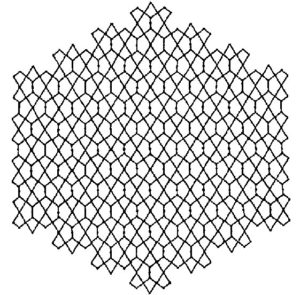
Figure 2. Dominating David derived network of the second type \(D_{2}(2)\)
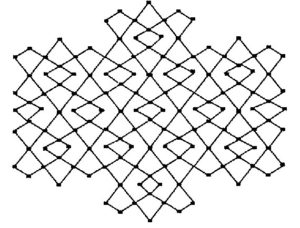
Figure 3. Dominating David derived network of the third type \(D_{3}(2)\)
Theorem 1.1 Let \(G=D_{1}(n)\) be the dominating David derived network of \(1^{st}\) type. Then the first and the second \(K\)-Banhatti indices of \(D_{1}(n)\) are \begin{eqnarray*} B_{1}[D_{1}(n)]&=&1485n^{2}+1624n-1002\\ B_{2}[D_{1}(n)]&=&3204n^{2}+764n-3292 \end{eqnarray*}
Proof. Let \(G=D_{1}(n)\) be the dominating David derived network of \(1^{st}\) type. From figure 1, the edge partition of dominating David derived network of \(1^{st}\) type \(D_{1}(n)\) based on degrees of end vertices of each edge is give in table 1.
Edge partition of Dominating David derived network of first type
| \((d_{u}, d_{v})\) | Number of edges | Degree of Edges |
|---|---|---|
| \((2,2)\) | \(4n\) | \(2\) |
| \((2,3)\) | \(4n-4\) | \(3\) |
| \((2,4)\) | \(28n-16\) | \(4\) |
| \((3,3)\) | \(9n^{2}-13n+24\) | \(4\) |
| \((3,4)\) | \(36n^{2}-56n+24\) | \(5\) |
| \((4,4)\) | \(36n^{2}-56n+20\) | \(6\) |
Theorem 1.2. Let \(G=D_{1}(n)\) be the dominating David derived network of \(1^{st}\) type. Then the first and the second \(K\)-hyper Banhatti indices of \(D_{1}(n)\) are \begin{eqnarray*} HB_{1}[D_{1}(n)]&=&13302n^{2}-16623n+6146\\ HB_{2}[D_{1}(n)]&=&66564n^{2}-89092n+33892 \end{eqnarray*}
Proof Let \(G=D_{1}(n)\) be the dominating David derived network of \(1^{st}\) type. Then first \(K\)-hyper Banhatti index of \(D_{1}(n)\) is calculated as \begin{eqnarray*} HB_{1}[D_{1}(n)]&=&\sum\limits_{ue}[d_{G}(u)+d_{G}(v)]^{2}\\ &=&\sum\limits_{ue\in E_{2,2}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+ \sum\limits_{ue\in E_{2,3}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{2,4}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{3,3}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{3,4}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{4,4}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &=& 4n[(2+2)^{2}+(2+2)^{2}]+(4n-4)[(2+3)^{2}+(3+3)^{2}]\\ &&+(28n-16)[(2+4)^{2}+(4+4)^{2}]\\ &&+(9n^{2}-13n+24)[(3+4)^{2}+(3+4)^{2}]\\ &&+(36n^{2}-56n+24)[(3+5)^{2}+(4+5)^{2}]\\ &&+(36n^{2}-56n+20)[(4+6)^{2}+(4+6)^{2}]\\ &=& 13302n^{2}-16623n+6146 \end{eqnarray*} Second \(K\)-hyper Banhatti index of \(D_{1}(n)\) is calculated as \begin{eqnarray*} HB_{2}[D_{1}(n)]&=&\sum\limits_{ue}[d_{G}(u)d_{G}(v)]^{2}\\ &=&\sum\limits_{ue\in E_{2,2}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+ \sum\limits_{ue\in E_{2,3}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{2,4}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{3,3}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{3,4}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{4,4}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &=& 4n[4^{2}+4^{2}]+(4n-4)[6^{2}+9^{2}]\\ &&+(28n-16)[8^{2}+16^{2}]\\ &&+(9n^{2}-13n+24)[12^{2}+12^{2}]\\ &&+(36n^{2}-56n+24)[15^{2}+20^{2}]\\ &&+(36n^{2}-56n+20)[24^{2}+24^{2}]\\ &=& 66564n^{2}-89092n+33892. \end{eqnarray*}
Theorem 1.3. Let \(G=D_{2}(n)\) be the dominating David derived network of \(2^{nd}\) type. Then the first and the second \(K\)-Banhatti indices of \(D_{2}(n)\) are \begin{eqnarray*} B_{1}[D_{2}(n)]&=&1530n^{2}-1810n+650\\ B_{2}[D_{2}(n)]&=&32584n^{2}-4127n+1506 \end{eqnarray*}
Proof Let \(G=D_{2}(n)\) be the dominating David derived network of \(2^{nd}\) type. Table \(2\) shows the edge partition of dominating David derived network of \(2^{nd}\) type \(D_{2}(n)\) based on degrees of end vertices of each edge
Edge partition of Dominating David derived network of second type
| \((d_{u}, d_{v})\) | Number of edges | Degree of Edges |
|---|---|---|
| \((2,2)\) | \(4n\) | \(2\) |
| \((2,3)\) | \(18n^{2}-22n+6\) | \(3\) |
| \((2,4)\) | \(28n-16\) | \(4\) |
| \((3,4)\) | \(36n^{6}-56n+24\) | \(5\) |
| \((4,4)\) | \(336n^{6}-56n+20\) | \(6\) |
Theorem 1.4. Let \(G=D_{2}(n)\) be the dominating David derived network of \(2^{nd}\) type. Then the first and the second \(K\)-hyper Banhatti indices of \(D_{2}(n)\) are \begin{eqnarray*} HB_{1}[D_{1}(n)]&=&1351n^{2}-1693n+6246\\ HB_{2}[D_{1}(n)]&=&22606n^{2}-28486n+10582 \end{eqnarray*}
Proof Let \(G=D_{2}(n)\) be the dominating David derived network of \(2^{nd}\) type. First \(K\)- hyper Banhatti index of \(D_{2}(n)\) is calculated as \begin{eqnarray*} HB_{1}[D_{2}(n)]&=&\sum\limits_{ue}[d_{G}(u)+d_{G}(v)]^{2}\\ &=&\sum\limits_{ue\in E_{2,2}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+ \sum\limits_{ue\in E_{2,3}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{2,4}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{3,4}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{4,4}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &=& 4n[(2+2)^{2}+(2+2)^{2}]+(18n^{2}-22n+6)[(2+3)^{2}+(3+3)^{2}]\\ &&+(28n-16)[(2+4)^{2}+(4+4)^{2}]\\ &&+(36n^{6}-56n+24)[(3+5)^{2}+(4+5)^{2}]\\ &&+(36n^{6}-56n+20)[(4+6)^{2}+(4+6)^{2}]\\ &=& 1351n^{2}-1693n+6246. \end{eqnarray*} Second \(K\)-hyper Banhatti index of \(D_{2}(n)\) is calculated as \begin{eqnarray*} HB_{2}[D_{2}(n)]&=&\sum\limits_{ue}[d_{G}(u)d_{G}(v)]^{2}\\ &=&\sum\limits_{ue\in E_{2,2}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+ \sum\limits_{ue\in E_{2,3}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{2,4}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{3,4}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{4,4}}[(d_{G}(u)d_{G}(e)^{2})+(d_{G}(v)d_{G}(e))^{2}]\\ &=& 4n[(2.2)^{2}+(2.2)^{2}]+(18n^{2}-22n+6)[(2.3)^{2}+(3.3)^{2}]\\ &&+(28n-16)[(2.4)^{2}+(4.4)^{2}]\\ &&+(36n^{6}-56n+24)[(3.5)^{2}+(4.5)^{2}]\\ &&+(36n^{6}-56n+20)[(4.6)^{2}+(4.6)^{2}]\\ &=& 22606n^{2}-28486n+10582. \end{eqnarray*}
Theorem 1.5 Let \(G=D_{3}(n)\) be the dominating David derived network of \(3^{rd}\) type. Then the first and the second $K$-Banhatti indices of \(D_{3}(n)\) are \begin{eqnarray*} B_{1}[D_{3}(n)]&=&1944n^{2}-2128n+600\\ B_{2}[D_{3}(n)]&=&4320n^{2}-8224n+2112 \end{eqnarray*}
Proof Let \(G=D_{3}(n)\) be the dominating David derived network of \(3^{rd}\) type. Table \(3\) shows the edge partition of dominating David derived network of \(3^{rd}\) type \(D_{3}(n)\) based on degrees of end vertices of each edge.
Edge partition of Dominating David derived network of second type
| \((d_{u}, d_{v})\) | Number of edges | Degree of Edges |
|---|---|---|
| \((2,2)\) | \(4n\) | \(2\) |
| \((2,4)\) | \(36n^{2}-20n\) | \(4\) |
| \((4,4)\) | \(72n^{2}-108n+44\) | \(6\) |
Theorem 1.6. Let \(G=D_{3}(n)\) be the dominating David derived network of \(3^{rd}\) type. Then the first and the second \(K\)-hyper Banhatti indices of \(D_{3}(n)\) are \begin{eqnarray*} HB_{1}[D_{3}(n)]&=&18000n^{2}-23472n+8800\\ HB_{2}[D_{3}(n)]&=&94464n^{2}-130688n+50688 \end{eqnarray*}
Proof. Let \(G=D_{3}(n)\) be the dominating David derived network of \(3^{rd}\) type. Then the first \(K\)-hyper Banhatti index is calculated as \begin{eqnarray*} HB_{1}[D_{3}(n)]&=&\sum\limits_{ue}[d_{G}(u)+d_{G}(v)]^{2}\\ &=&\sum\limits_{ue\in E_{2,2}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+ \sum\limits_{ue\in E_{2,4}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{4,4}}[(d_{G}(u)+d_{G}(e))^{2}+(d_{G}(v)+d_{G}(e))^{2}]\\ &=& 4n[(2+2)^{2}+(2+2)^{2}]+(36n^{2}-20n)[(2+4)^{2}+(4+4)^{2}]\\ &&+(72n^{2}-108n+44)[(2+6)^{2}+(4+6)^{2}]\\ &=& 18000n^{2}-23472n+8800 \end{eqnarray*} Second \(K\)-hyper Banhatti index of \(D_{3}(n)\) is calculated as \begin{eqnarray*} HB_{1}[D_{3}(n)]&=&\sum\limits_{ue}[d_{G}(u)+d_{G}(v)]^{2}\\ &=&\sum\limits_{ue\in E_{2,2}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+ \sum\limits_{ue\in E_{2,4}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &&+\sum\limits_{ue\in E_{4,4}}[(d_{G}(u)d_{G}(e))^{2}+(d_{G}(v)d_{G}(e))^{2}]\\ &=& 4n[(2.2)^{2}+(2.2)^{2}]+(36n^{2}-20n)[(2.4)^{2}+(4.4)^{2}]\\ &&+(72n^{2}-108n+44)[(2.6)^{2}+(4.6)^{2}]\\ &=& 94464n^{2}-130688n+50688 \end{eqnarray*}
Conclusion
In the present report, we have computed First and second K-Banhatti and K-hyer Banhatti indices of Dominating David derived networks of first, second and third type.2. Competing Interests
The author do not have any competing interests in the manuscript.References
- West, D. B. (2001). Introduction to graph theory (Vol. 2). Upper Saddle River: Prentice hall. [Google Scholor]
- Rücker, G., & Rücker, C. (1999). On topological indices, boiling points, and cycloalkanes. Journal of chemical information and computer sciences, 39(5), 788-802. [Google Scholor]
- Klavžar, S., & Gutman, I. (1996). A comparison of the Schultz molecular topological index with the Wiener index. Journal of chemical information and computer sciences, 36(5), 1001-1003. [Google Scholor]
- Wiener, H. (1947). Structural determination of paraffin boiling points. Journal of the American Chemical Society, 69(1), 17-20. [Google Scholor]
- Dobrynin, A. A., Entringer, R., & Gutman, I. (2001). Wiener index of trees: theory and applications. Acta Applicandae Mathematicae, 66(3), 211-249. [Google Scholor]
- Gutman, I., & Polansky, O. E. (2012). Mathematical concepts in organic chemistry. Springer Science & Business Media. [Google Scholor]
- Randic, M. (1975). Characterization of molecular branching. Journal of the American Chemical Society, 97(23), 6609-6615. [Google Scholor]
- Bollobás, B., & Erdös, P. (1998). Graphs of extremal weights. Ars Combinatoria, 50, 225-233. [Google Scholor]
- Amic, D., Bešlo, D., Lucic, B., Nikolic, S., & Trinajstic, N. (1998). The vertex-connectivity index revisited. Journal of chemical information and computer sciences, 38(5), 819-822. [Google Scholor]
- Hu, Y., Li, X., Shi, Y., Xu, T., & Gutman, I. (2005). On molecular graphs with smallest and greatest zeroth-order general Randic index. MATCH Commun. Math. Comput. Chem, 54(2), 425-434. [Google Scholor]
- Sardar, M. S, Zafar, S., & Farahani, M. R. (2017). The generalized zagreb index of capra-designed planar benzenoid series \(ca_k(c_6)\), Open J. Math. Sci., 1(1), 44-51.[Google Scholor]
- Rehman, H. M, Sardar, R., Raza, A. (2017). Computing topological indices of hex board and its line graph. Open J. Math. Sci., 1(1), 62- 71.[Google Scholor]
- Kulli, V. R., Chaluvaraju, B., & Boregowda, H. S. (2017). Connectivity Banhatti indices for certain families of benzenoid systems. Journal of Ultra Chemistry, 13(4), 81-87. [Google Scholor]
- Imran, M., Baig, A. Q., & Ali, H. (2015). On topological properties of dominating David derived networks. Canadian Journal of Chemistry, 94(2), 137-148. [Google Scholor]
- Simonraj, F., & George, A. (2012). Embedding of poly honeycomb networks and the metric dimension of star of david network. International Journal on Applications of Graph Theory in Wireless Ad Hoc Networks and Sensor Networks, 4(4), 11. [Google Scholor]