Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2022.0175
Steady-state solutions for modified Stokes’ second problem of Maxwell fluids with power-law dependence of viscosity on the pressure
Constantin Fetecau\(^{1,*}\) and Dumitru Vieru\(^2\)
\(^1\) Section of Mathematics, Academy of Romanian Scientists, 54 Splaiul Independentei, 050094 Bucharest, Romania.
\(^2\) Department of Theoretical Mechanics, Technical University of Iasi, 67 Bd. Dimitrie Mangeron.
Correspondence should be addressed to Constantin Fetecau at c_fetecau@yahoo.com
Abstract
Keywords:
1. Introduction
The motion of fluid over an infinite plate oscillating in its plane is termed as Stokes' second problem by Schlichting [1]. It is termed as the modified Stokes' second problem by Rajagopal et al., [2] if the fluid is bounded by two parallel walls. Both motions are important from the theoretical and practical point of view because they appear in many applied problems, such as flows in vibrating media. If the fluid has been at rest up to the initial moment, its motion becomes steady in time and a very important problem for experimentalists is to know the time after which the steady or permanent state is obtained. To determine this time, at least the steady-state (permanent or long-time) solutions have to be known.
The fact that the fluid viscosity could depend on the pressure was early enough suggested by Stokes [3] and the experimental investigations (see for instance Bridgman [4], Cutler et al., [5], Johnson and Tewaarwerk [6], Bair and Winer [7] and Prusa et al., [8] have certified this supposition. For instance, in elastohydrodynamic lubrication problems, the effects of pressure on viscosity cannot be neglected. Concerning the importance of the pressure- dependent viscosity in steady motions of incompressible fluids, we recommend the paper of Huilgol, and You [9]. On the other hand, Kannan and Rajagopal [10] remarked that gravity has a notable influence in different motions with engineering applications. Its effects are more pronounced if the pressure alters along the direction in which the gravity acts. First exact solutions for steady motions of incompressible Newtonian fluids with pressure-dependent viscosity in which the influence of gravity is taken into consideration are those of Rajagopal [11,12]. Interesting steady and starting solutions for the modified Stokes' problems of Newtonian fluids with pressure-dependent viscosity have also been established by Prusa [13], respectively Rajagopal et al., [12] when the gravity effects are taken into consideration. Recently, permanent solutions corresponding to motions of incompressible Newtonian fluids with power-law dependence of viscosity on the pressure have been determined by Fetecau, and Agop [14], Fetecau and Vieru [15], and Fetecau and Rauf [16]. Some of them have already been extended to incompressible Maxwell fluids (IMF) of the same type [17,18,19].
The goal of this work is to provide closed-form expressions for the steady-state solutions corresponding to the modified Stokes' second problem and the simple Couette flow for a class of IMF with power-law dependence of viscosity on the pressure. Analytical expressions are established for the dimensionless velocity fields and the corresponding nontrivial shear and normal stresses. For a check of their correctness, it was graphically proved that the diagrams of the solutions corresponding to the motion induced by cosine oscillations of the plate are almost identical to those of the simple Couette flow if the oscillations' frequency is small enough. In addition, similar solutions for ordinary IMF and incompressible Newtonian fluids (IMF) with power-law dependence of viscosity on the pressure performing the same motions are obtained as limiting cases of general results. The influence of the main parameters on the fluid motion is graphically underlined and discussed.
2. Formulation of the problem
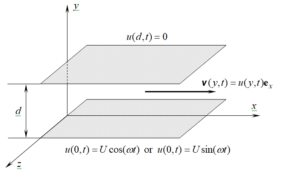
Let us consider an IMF with pressure-dependent viscosity at rest between two infinite horizontal parallel plates at the distance d one of the other as it is illustrated in Figure 1. Its constitutive equations, as they have been presented by Karra et al., [20], are given by the following relationswhere \(\alpha\) is the pressure-viscosity coefficient and \(\mu\) is the fluid viscosity at the reference pressure \(p_{0}\). We shall refer to the Lagrange multiplier p as pressure although, for such fluids, it is not the mean normal stress [20].
Figure 1. Geometry of the flow.
If \(\lambda \rightarrow 0\) in the equality \((1)_{2}\), the new constitutive equations (1) define incompressible Newtonian fluids (INF) with pressure-dependent viscosity. If \(\alpha = 0\) in Eq. (2) \(\eta(p) = \mu\) and the adequate constitutive equations (1) correspond to ordinary IMF. The fact that \(\eta(p) \rightarrow \infty\) for \(p \rightarrow \infty\) is in accordance with a property that have been experimentally confirmed.
At the moment \(t = 0^{+}\) the lower plate begins to oscillate in its plane according to
3. Solution of the problem
In order to evade possible confusions, we denote by \(u_{c}(y,t)\), \(\tau_{c}(y,t)\), \(\sigma_{c}(y,t)\) and \(u_{s}(y,t)\), \(\tau_{s}(y,t)\), \(\sigma_{s}(y,t)\) the dimensionless starting solutions corresponding to the two motions induced by cosine, respectively sine oscillations of the lower plate. These solutions can be represented as sums of their permanent and transient components, namelyThe complex velocity \(u_{p}(y,t)\) has to satisfy the following boundary value problem
3.1. Calculation of the complex velocity \(u_{p}(y,t)\)
By substituting \(u_{p}(y,t)\) from Eq. \((26)_{1}\) in (22) and (23), one obtains for the function \(V(y)\) the following ordinary differential equation with boundary conditions3.2. Calculation of the complex stresses \(\tau_{p}(y,t)\) and \(\sigma_{p}(y,t)\)
By derivation of the equality (32) with respect to y one obtains4. Results' validation
In order to validate the correctness of results which have been here obtained, we shall compare their limits for \(\alpha \rightarrow 0\) or \(\omega \rightarrow 0\) with known results from the literature, respectively with the similar solutions corresponding to the simple Couette flow of the same fluids.4.1. Case \(\alpha \rightarrow 0\); Modified Stokes' second problem for ordinary IMF
Using convenient asymptotic approximations of the Bessel functions, namelySimilar computations show that the stresses \(\tau_{\text{cp}}(y,t)\), \(\tau_{\text{sp}}(y,t)\), \(\sigma_{\text{cp}}(y,t)\) and \(\sigma_{\text{sp}}(y,t)\) can be approximated by the following relations:
4.2. Case \(\omega \rightarrow 0\); Simple Couette flow of IMF with power-law dependence of viscosity on the pressure
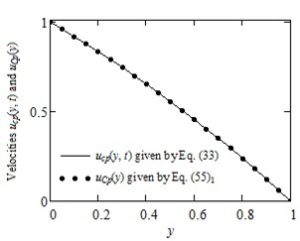
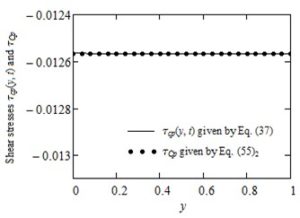
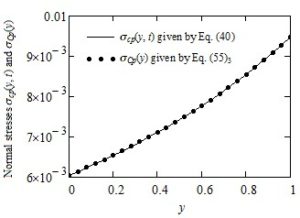
The dimensionless permanent solutions corresponding to the simple Couette flow of IMF with power-law dependence of the form (2) of velocity on the pressure, namelycan be easily determined successively solving the corresponding governing equations. As expected, Figures 2-4 show that the diagrams of \(u_{\text{cp}}(y,t)\), \(\tau_{\text{cp}}(y,t)\) and \(\sigma_{\text{cp}}(y,t)\) are almost identical to those of \(u_{\text{Cp}}(y),\text{ }\tau_{\text{Cp}}\), respectively \(\sigma_{\text{Cp}}(y)\) if the frequency \(\omega\) of the oscillations as well as the product \(\omega\)t is small enough. A surprising result is the fact that the permanent shear stress \(\tau_{\text{Cp}}\) corresponding to the simple Couette flow of such fluids is constant on the whole flow domain although the fluid velocity \(u_{\text{Cp}}(y)\) and the corresponding normal stress \(\sigma_{\text{Cp}}(y)\) are functions of the spatial variable y. However, this shear stress as well as the fluid velocity and the normal stress depend on the pressure-viscosity coefficient.
Figure 2. Comparison between the permanent the velocities \(u_{\text{cp}}(y,t)\) and \(u_{\text{Cp}}(y)\) for \(\text{Re} = 100,\text{\ \ }\text{We} = 0.3,\ \ \alpha = 0.4,\ \ \omega = 0.001\) and \(t = 10\)}
Figure 3. Comparison between the shear stresses\(\tau_{\text{cp}}(y,t)\) and \(\tau_{\text{Cp}}\) for \(\text{Re} = 100,\text{\ \ }\text{We} = 0.3,\ \ \alpha = 0.4,\ \ \omega = 0.001\) and \(t = 10\)}
Figure 4. Comparison between the normal stresses \(\sigma_{\text{cp}}(y,t)\) and \(\sigma_{\text{Cp}}(y)\) for \(\text{Re} = 100,\text{\ \ }\text{We} = 0.3,\ \ \alpha = 0.4,\ \ \omega = 0.001\) and \(t = 10\)}
4.3. Case \(\alpha \rightarrow 0\) and \(\omega \rightarrow 0\) Simple Couette flow of ordinary IMF
Finally, making \(\omega \rightarrow 0\) in Eqs. \((52)_{1}\), (57) and (59) or \(\alpha \rightarrow 0\) in Eqs. (61) one obtains the steady solutions corresponding to the simple Couette flow of ordinary IMF, namely5. Some numerical results and conclusions
The main purpose of this note is to offer a simple alternative for those who want to find the necessary time to reach the permanent state (steady state) corresponding to the modified Stokes' second problem of some IMF with power-law dependence of viscosity on the pressure. To do that, exact expressions are established for the dimensionless permanent solutions corresponding to the velocity field and the non-trivial shear and normal stresses. The required time to touch the permanent state can be graphically determined by comparing these solutions with the corresponding starting solutions (numerical solutions). It is the time after which the diagrams of starting solutions superpose over those of the permanent solutions and the fluid behavior is characterized by the steady-state solutions only.For completion, as well as for a check of the correctness of results that have been here obtained; exact expressions are also determined for the similar solutions correspond to the simple Couette flow of the same fluids. Figures 2-4, as it was to be expected, clearly show that for a small enough value of the oscillations' frequency \(\omega\) the diagrams of solutions \(u_{\text{cp}}(y,t)\), \(\tau_{\text{cp}}(y,t)\) and \(\sigma_{\text{cp}}(y,t)\) are almost identical to those of the simple Couette flow \(u_{\text{Cp}}(y)\), \(\tau_{\text{Cp}}\) and \(\sigma_{\text{Cp}}(y)\), respectively. The dimensionless steady state solutions corresponding to the ordinary IMF performing the same motions, as well as those of the INF with power-law dependence of viscosity on the pressure is obtained as limiting cases of the initial solutions.
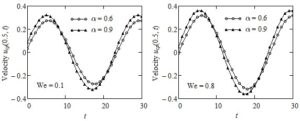
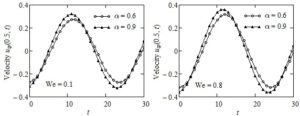
In order to bring to light the influence of Weissenberg number We and of the pressure-viscosity coefficient \(\alpha\) on the fluid motion Figures 5 and 6 and Table 1 have been included here. In these figures the time variations of the mid plane velocities \(u_{\text{cp}}(0.5,t)\) and \(u_{\text{sp}}(0.5,t)\) are presented at distinct values of the two parameters. Oscillatory specific features of the two motions and the phase difference between them are clearly visualized. It also results that the order of magnitude of the oscillations' amplitude for common values of the parameters is the same for both movements and the smaller values of pressure-viscosity coefficient \(\alpha\) or We the smaller the oscillations' amplitude. Consequently, the fluid decelerates for decreasing values of the two parameters, and the lowest velocity corresponds to the ordinary IMF, respectively the INF with pressure-dependent viscosity. As regards the Weissenberg number We, as it was proved by Poole [23], it represents the ratio of elastic to viscous forces. Therefore, at the same elastic properties of the fluid, a decline of We means an increase of viscous forces, which implies a decrease of the fluid velocity. In Table 1, for completion, numerical values of the dimensionless steady velocity \(u_{\text{Cp}}(y)\) corresponding to the simple Couette flow of IMF with power-law dependence of viscosity on the pressure are provided at three values of the pressure-viscosity coefficient \(\alpha\) and different values of the spatial variable y. The fluid velocity, as before, grows for increasing values of \(\alpha\).
Figure 5. Profiles of velocities \(u_{\text{cp}}(0.5,t)\) for \(\text{Re} = 100,\ \ \omega = \pi/12,\) \(\ \alpha = 0.6\) and \(\ \alpha = 0.9\) and two values of Weissenberg number We.
Figure 6. Profiles of velocities \(u_{\text{sp}}(y,t)\) for \(\text{Re} = 100,\ \ \omega = \pi/12,\)\(\ \alpha = 0.6\) and \(\ \alpha = 0.9\) and two values of Weissenberg number We.
Table 1.
| y | \(u_{Cp}(y)\) | ||
|---|---|---|---|
| \(\alpha=0.2\) | \(\alpha=0.5\) | \(\alpha=0.9\) | |
| 0 | 1 | 1 | 1 |
| 0.1 | 0.910 | 0.921 | 0.932 |
| 0.2 | 0.819 | 0.839 | 0.859 |
| 0.3 | 0.725 | 0.753 | 0.780 |
| 0.4 | 0.629 | 0.662 | 0.696 |
| 0.5 | 0.530 | 0.567 | 0.605 |
| 0.6 | 0.430 | 0.466 | 0.506 |
| 0.7 | 0.326 | 0.360 | 0.398 |
| 0.8 | 0.220 | 0.247 | 0.279 |
| 0.9 | 0.112 | 0.128 | 0.147 |
| 1 | 0 | 0 | 0 |
The main results that have been obtained by means of the present study are:
- Exact expressions have been established for the steady-state solutions of the modified Stokes' second problem of IMF with power-law dependence of viscosity on the pressure.
- Oscillatory behavior of the two motions and the influence of Weissenberg number and the pressure-viscosity coefficient on fluid velocity was graphically underlined and discussed.
- Similar solutions corresponding to the same problem of ordinary IMF and of INF with power-law dependence of viscosity on the pressure have been obtained as limiting cases of the present results using suitable asymptotic approximations of Bessel functions.
- Steady solutions for the simple Couette flow of IMF with power-law dependence of viscosity on the pressure have been also determined and the convergence of \(u_{\text{cp}}(y,t)\), \(\tau_{\text{cp}}(y,t)\) and \(\sigma_{\text{cp}}(y,t)\) to these solutions was graphically proved when \({ \omega \rightarrow}\mathbf{0}\).
- The shear stress \(\tau_{\text{Cp}}\) corresponding to this motion is constant on the entire flow domain although the velocity \(u_{\text{Cp}}(y)\) and normal stress \(\sigma_{\text{Cp}}(y)\) are functions of the spatial variable y.
Acknowledgments
The authors would like to thank reviewers for their careful assessment, valuable suggestions and comments regarding the initial version of the manuscript.Conflicts of Interest:
"The author declares no conflict of interest."References
- Schlichting, H. (1968). Boundary Layer Theory. McGraw-Hill, Singapore. [Google Scholor]
- Rajagopal, K. R., Saccomandi, G., & Vergori, L. (2013). Unsteady flows of fluids with pressure dependent viscosity. Journal of Mathematical Analysis and Applications, 404(2), 362-372. [Google Scholor]
- Stokes, G. G. (2007). On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids. Transactions of the Cambridge Philosophical Society, 8, 287-305, 1845. [Google Scholor]
- Bridgman, P. W. (1931). The Physics of High Pressure. The MacMillan Company, New York. [Google Scholor]
- Cutler, W. G., McMickle, R. H., Webb, W., & Schiessler, R. W. (1958). Study of the compressions of several high molecular weight hydrocarbons. The Journal of Chemical Physics, 29(4), 727-740. [Google Scholor]
- Johnson, K. L., & Tevaarwerk, J. L. (1977). Shear behaviour of elastohydrodynamic oil films. Proceedings of the Royal Society of London. A. Mathematical and Physical Sciences, 356(1685), 215-236. [Google Scholor]
- Bair, S., & Winer, W. O. (1992). The high pressure high shear stress rheology of liquid lubricants. Journal of Tribology, 114, 1-13. [Google Scholor]
- Pruša, V., Srinivasan, S., & Rajagopal, K. R. (2012). Role of pressure dependent viscosity in measurements with falling cylinder viscometer. International Journal of Non-Linear Mechanics, 47(7), 743-750. [Google Scholor]
- Huilgol, R. R., & You, Z. (2006). On the importance of the pressure dependence of viscosity in steady non-isothermal shearing flows of compressible and incompressible fluids and in the isothermal fountain flow. Journal of non-newtonian fluid mechanics, 136(2-3), 106-117. [Google Scholor]
- Kannan, K., & Rajagopal, K. R. (2005). Flows of fluids with pressure dependent viscosities between rotating parallel plates. In: P. Fergola et al. (Eds.), New Trends in Mathematical Physics, World Scientific, Singapore. [Google Scholor]
- Rajagopal, K. R. (2004). Couette flows of fluids with pressure dependent viscosity. International Journal of Applied Mechanics and Engineering, 9(3), 573-585. [Google Scholor]
- Rajagopal, K. R. (2008). A semi-inverse problem of flows of fluids with pressure-dependent viscosities. Inverse Problems in Science and Engineering, 16(3), 269-280. [Google Scholor]
- Pruša, V. (2010). Revisiting Stokes first and second problems for fluids with pressure-dependent viscosities. International Journal of Engineering Science, 48(12), 2054-2065. [Google Scholor]
- Fetecau, C., & Agop, M. (2020). Exact solutions for oscillating motions of some fluids with power-law dependence of viscosity on the pressure. Annals of the Academy of Romanian Scientists: Series on Mathematics and its Applications, 12, 295-311. [Google Scholor]
- Fetecau, C., & Vieru, D. (2020). Exact solutions for unsteady motion between parallel plates of some fluids with power-law dependence of viscosity on the pressure. Applications in Engineering Science, 1, 100003, https://doi.org/10.1016/j.apples.2020.100003. [Google Scholor]
- Fetecau, C., Rauf, A., Qureshi, T. M., & Khan, M. (2020). Permanent solutions for some oscillatory motions of fluids with power-law dependence of viscosity on the pressure and shear stress on the boundary. Zeitschrift für Naturforschung A, 75(9), 757-769. [Google Scholor]
- Fetecau, C., & Rauf, A. (2021). Permanent solutions for some motions of UCM uids with power-law dependence of viscosity on the pressure. Studia Universitatis Babes-Bolyai, Mathematica, 66(1), 197-209. [Google Scholor]
- Fetecau, C.,Vieru, D., Rauf, A., & Qureshi, T. M.(2021). Steady-state solutions for some motions of Maxwell fluids with pressure-dependence of viscosity. Journal of Mathematical Sciences: Advances and Applications, 68, 1-28. [Google Scholor]
- Fetecau, C., Qureshi, T. M., Rauf, A., & Vieru, D. (2022). On the modified stokes second problem for maxwell fluids with linear dependence of viscosity on the pressure. Symmetry, 14(2), Article No. 219, https://doi.org/10.3390/sym14020219.[Google Scholor]
- Karra, S., Pruša, V., & Rajagopal, K. R. (2011). On Maxwell fluids with relaxation time and viscosity depending on the pressure. International Journal of Non-Linear Mechanics, 46(6), 819-827. [Google Scholor]
- Fetecau, C., Ellahi, R., & Sait, S. M. (2021). Mathematical analysis of Maxwell fluid flow through a porous plate channel induced by a constantly accelerating or oscillating wall. Mathematics, 9(1), Article No. 90, https://doi.org/10.3390/math9010090. [Google Scholor]
- Erdogan, M. E. (2002). On the unsteady unidirectional flows generated by impulsive motion of a boundary or sudden application of a pressure gradient. International Journal of Non-Linear Mechanics, 37(6), 1091-1106. [Google Scholor]
- Poole, R. J. (2012). The deborah and weissenberg numbers. Rheology Bulletin, 53(2), 32-39. [Google Scholor]