Open Journal of Discrete Applied Mathematics
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2022.0072
Sombor indices – back to geometry
Ivan Gutman
Faculty of Science, University of Kragujevac, Kragujevac, Serbia.; gutman@kg.ac.rs
Abstract
Keywords:
1. Introduction
In this paper, we are concerned with a geometric interpretation of vertex-degree-based topological indices, extending the considerations from Ref. [1]. Let \(G\) be a simple graph with vertex set \(\mathbf V(G)=\{v_1,v_2,\ldots,v_n\}\) and edge set \(\mathbf E(G)\). The degree (= number of first neighbors) of the vertex \(v_i \in \mathbf V(G)\) will be denoted by \(d_i\). If the vertices \(v_i\) and \(v_j\) are adjacent, then the edge connecting them is labeled by \(ij\).
In the mathematical and chemical literature, several dozens of vertex-degree-based (VDB) graph invariants (usually referred to as ''topological indices'') have been introduced and extensively studied [1,2,3,4]. Their general formula is
Some of these VDB indices, mentioned in the later part of the paper, are the first and second Zagreb index [5,6]
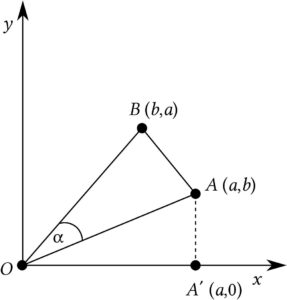
The distance between the degree-point of the edge \(ij\) (denoted by \(A\) in Figure 1), and the origin (\(O\)), assuming an Euclidean metrics, is \(\sqrt{d_i^2+d_j^2}\). Summing this over all edges of the graph \(G\), one obtains the right-hand side of Eq. (4), i.e., the Sombor index [1].
We indicate this transformation as
Figure 1. A geometric representation of an edge \(e=ij\) of the graph \(G\), connecting vertices of degree \(d_i=a\) and \(d_j=b\) \ (\(a > b)\). The point \(A\) represents the edge \(ij\), whereas the point \(B\) is the respective dual. \(O\) denotes the origin of the coordinate system.
In fact, the Sombor index was actually conceived by using the above geometric considerations [1]. This VDB topological index soon attracted much attention, and its numerous mathematical [8,9,10,11,12,13,14] and chemical [15,16,17,18,19] applications have been established. Yet, with a single exception [20], the geometry-based features of the Sombor index were ignored, and only its algebraic and combinatorial aspects were in focus of interest.
In this paper we intend to point out the great variety of Sombor-index-like VDB graph invariants that can be constructed by means of geometric arguments.
First of all, we recall that in [1], it was shown that the distance between the degree-point and its dual (points \(A\) and \(B\) in Figure 1), is equal to \(\sqrt{2}\,\big|d_i-d_j \big|\), which after adding over all edges yields the Albertson index, i.e., \(\sqrt{2}\,Alb(G)\), cf. Eq. (3). In analogy to formula (5), we write this as:
Thus, a few classical VDB topological indices have a geometry-based interpretation.
2. More Sombor-index-like graph invariants
In this section we consider the triangle formed by the degree-point, dual-degree-point, and the origin of the coordinate system, points \(A\), \(B\), and \(O\) in Figure 1. From this triangle, we generate a number of new Sombor-index-like VDB invariants, denoted below by \(SO_1,SO_2,\ldots,SO_6\).First note that by bearing in mind Eqs. (5) and (6), we immediately get
\[ \sum_{ij \in \mathbf E(G)} perim(ABO) = 2\,SO(G) + \sqrt{2}\,Alb(G)\,. \] Using elementary geometry (Heron's formula), knowing the distance between the points \(A\) and \(O\) (same as between \(B\) and \(O\)), cf. Eq. (5), as well as between \(A\) and \(B\), cf. Eq. (6), we obtain \[ area(ABO) = \frac{1}{2}\,\big(a^2-b^2 \big)\,, \] from which it follows \[ \sum_{ij \in \mathbf E(G)} area(ABO) = \sum_{ij \in \mathbf E(G)} \frac{1}{2}\,\big|d_i^2 - d_j^2 \big| := SO_1(G)\,. \] Let \(\alpha\) be the angle between the lines \(OA\) and \(OB\), see Figure 1. Using the classical formula \[ area(ABO) = \frac{1}{2}\,dist(OA)\,dist(OB)\,\sin \alpha\,, \] we get \[ \frac{1}{2}\,\big| d_i^2-d_j^2 \big| = \frac{1}{2}\,\left( \sqrt{d_i^2+d_j^2} \right)^2\,\sin \alpha \,,\] from which \[ \sum_{ij \in \mathbf E(G)} \sin \alpha = \sum_{ij \in \mathbf E(G)} \left| \frac{d_i^2 - d_j^2}{d_i^2+d_j^2} \right| := SO_2(G)\,. \] Denote by \(\Gamma_c\) the circumcircle (circumscribed circle) on the triangle \(ABO\). The respective incircle (inscribed circle) will be denoted by \(\Gamma_i\). Using elementary, yet somewhat lengthy, geometric reasoning, it can be shown thatConflicts of Interest:
''The author declares no conflict of interest.''References
- Gutman, I. (2021). Geometric approach to degree-based topological indices: Sombor indices. MATCH Communications in Mathematical and in Computer Chemistry, 86, 11-16. [Google Scholor]
- Gutman, I. (2013). Degree-based topological indices. Croatica Chemica Acta, 86, 351-361. [Google Scholor]
- Kulli, V. R. (2020). Graph indices. in: Pal, M., Samanta, S. & Pal, A. (Eds.), Handbook of Research of Advanced Applications of Graph Theory in Modern Society. Hershey: Global, pp. 66-91.[Google Scholor]
- Todeschini, R., & Consonni, V. (2009). Molecular Descriptors for Chemoinformatics. Weinheim: Wiley-VCH. [Google Scholor]
- Gutman, I., Rušcic, B., Trinajstic, N., & Wilcox, C. F. (1975). Graph theory and molecular orbitals. XII. Acyclic polyenes. Journal of Chemical Physics, 62, 3399-3405.[Google Scholor]
- Gutman, I. & Trinajstic, N. (1972). Graph theory and molecular orbitals. Total \(\pi\)-electron energy of alternant hydrocarbons. Chemical Physics Lettersm 17, 535-538. [Google Scholor]
- Albertson, M. O. (1997). The irregularity of a graph. Ars Combinatoria, 46, 219-225. [Google Scholor]
- Das, K. C., Çevik, A. S., Cangul, I. N. & Shang, Y. (2021). On Sombor index. Symmetry, 13(1), Article No. 140. https://doi.org/10.3390/sym13010140.[Google Scholor]
- Gutman, I. (2022). TEMO theorem for Sombor index. Open Journal of Discrete Applied Mathematics, 5(1), 25-28. [Google Scholor]
- Horoldagva, B., & Xu, C. (2021). On Sombor index of graphs. MATCH Communications in Mathematical and in Computer Chemistry, 86, 703-713. [Google Scholor]
- Ning, W., Song, Y., & Wang, K. (2022). More on Sombor index of graphs. Mathematics, 10(3), Article No. 301. https://doi.org/10.3390/math10030301. [Google Scholor]
- Ünal, S. O. (2022). Sombor index over the tensor and Cartesian product of monogenic semigroup graphs. Symmetry, 14(5), Article No. 1071. https://doi.org/10.3390/sym14051071. [Google Scholor]
- Rada, J., Rodríguez, J. M., & Sigarreta, J. M. (2021). General properties on Sombor indices. Discrete Applied Mathematics, 299, 87-97. [Google Scholor]
- Shang, Y. (2022). Sombor index and degree-related properties of simplicial networks. Applied Mathematics and Computation, 419, Article No. 126881. https://doi.org/10.1016/j.amc.2021.126881.[Google Scholor]
- Liu, H., Chen, H., Xiao, Q., Fang, X., & Tang, Z. (2021). More on Sombor indices of chemical graphs and their applications to the boiling point of benzenoid hydrocarbons. International Journal of Quantum Chemistry, 121(17), Article no. e26689. https://doi.org/10.1002/qua.26689. [Google Scholor]
- Redžepovic, I. (2021). Chemical applicability of Sombor indices. Journal of the Serbian Chemical Society, 86, 445-457. [Google Scholor]
- Alikhani, S., & Ghanbari, N. (2021). Sombor index of polymers. MATCH Communications in Mathematical and in Computer Chemistry, 86, 715-728. [Google Scholor]
- Amin, S., Ur Rehman Virk, A., Rehman, M. A. & Shah, N. A. (2021). Analysis of dendrimer generation by Sombor indices. Journal of Chemistry, 2021, Article No. 9930645. https://doi.org/10.1155/2021/9930645. [Google Scholor]
- Fang, X., You, L., & Liu, H. (2021). The expected values of Sombor indices in random hexagonal chains, phenylene chains and Sombor indices of some chemical graphs, International Journal of Quantum Chemistry, 121(17), Article No. e26740. https://doi.org/10.1002/qua.26740. [Google Scholor]
- Gutman, I. (2021). Some basic properties of Sombor indices. Open Journal of Discrete Applied Mathematics, 4(1), 1-3. [Google Scholor]
- Ali, A., Chartrand, G., & Zhang, P. (2021). Irregularity in Graphs. Cham: Springer. [Google Scholor]