Engineering and Applied Science Letter
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2022.0089
Algorithm analytic-numeric solution for nonlinear gas dynamic partial differential equation
Falade Kazeem Iyanda
Department of Mathematics, Faculty of Computing and Mathematical Sciences, Kano University of Science and Technology Wudil, P.M.B 3244 Kano State Nigeria.; faladekazeem2016@kustwudil.edu.ng
Abstract
Keywords:
1. Introduction
Gas dynamics is the science of the flow of air and other gas and or the notion of bodies through the air and other gas and its effects on physical systems, fluid mechanics, and thermodynamics; this science considers the products of combustion and combustion. The equations of gas dynamics are mathematical expressions based on the natural laws of conservations (mass, momentum, and energy). The study of shock fronts, rare fractions, and contact discontinuities are three major nonlinear wave equations that describe ideal gas dynamics behaviors [1]. Gas dynamics is synonymous with aerodynamics when the gas field is air, and the subject of study is flight. This is a core interest in aircraft and spacecraft design with their respective propulsion systems. Study in gas dynamics coincides with the developments of transonic and supersonic flight as the aircraft began to travel faster, and the density of air began to change, considerably increasing the air resistance as the airspeed approached the speed of sound. This phenomenon was later identified in wind tunnel experiments as an effect caused by the formation of shock waves around the aircraft. Major advances were made to describe the behavior during and after World War II, and the new understandings of compressible and high-speed flows became theories of gas dynamics [2].
In this paper, we consider nonlinear gas dynamic equation in one spatial dimension of the form:
In this paper, we construct a seven-step algorithm based on the modified new iterative method (MNIM) without using any transformation, linearization, and discretization for solving nonlinear gas-dynamic equation.
2. Method of solution
2.1. Modified new iterative method (MNIM)
The new iterative method (NIM) was proposed [11] and further improvement was made and applied to several ordinary differential equations, partial differential equations, and systems of partial differential equations. The MINM offers some certain advantages over routine numerical methods. For example, uses of discretization give rise to rounding off errors causing loss of accuracy and requiring considerable computational length and time. MNIM shows better performance since it does not involve discretization of the variables, is free from rounding off errors, and does not require more computational length to simplify the problems [12,13].Consider the new iterative method (NIM) as a numerical technique for solving an functional equation of the form
- Suppose \(g\left(x,t\right)\) is a smooth and nonhomogeneous function of the independent variable, \(x\) only, we include it in \(N\left(\psi\right)\).
- Suppose \(g\left(x,t\right)\) is a smooth and nonhomogeneous function of the independent variable, \(x\) and t, we include it in \(N\left(\psi\right)\).
- Suppose \(g\left(x,t\right)\) is a smooth and nonhomogeneous function are of \(x\),\(t\) and both \(x\) and \(t\) then we include in \(N\left(\psi\right)\) the terms involving \(t\) and both \(x\) and \(t\).
- Thus, the MNIM can be applied to obtain the close analytical solution.
2.2. Modified new iterative algorithm (MNIA)
In order to improve and reduce simplification involve in executing MNIM discussed in Section 2, we formulate seven steps algorithm using MAPLE 18 software commands to obtain numerical solution of nonlinear Gas dynamics equation (1).Algorithm 1. restart:
Step 1:
Digits:=35;
\(N:=R^{+};\)
\(\tau:=R^{+};\)
\(\psi\left(x,t_0\right):=h(x);\)
\(\psi\left[0\right]:=\psi (x,t_0);\)
Step 2:
\(GDPDE:=value(-\tau*\psi*diff(\psi[0],x)-\psi*(1-\psi)+g(x,t));\)
\(\psi\left[1\right]:=value(int(GDPDE,t=0...t));\)
Step 3:
for p from 1 to N do
\(\psi\left[p+1\right]:=value((int(((-\tau*(sum(\psi[n],n=0...p))*Diff(sum[n],n=0...p,x)-(sum(\psi[n],n=0...p))*\)
\((1-sum(\psi[n],n=0...p))+g(x,t))))-(int(((-\tau*(sum(\psi[n],n= 0...p-1))*Diff(sum(\psi[n],n=0...p-1,x)-(sum(\psi[n],n=0...p-1))*(1-sum(\psi[n],n=0...p-1))+g(x,t)))));\)
end do
Step 4:
\(Example:=evalf(sum(\psi[k],k=0...N+1))\)
Step 5: (11)
for i from 0 by 0.2 to 1 do\(\psi\left[i\right]:=evalf(eval(Example,[x=0.001,t=i]))\)
end do
Step 6:
for i from 0 by 2 to 10 do
\(N\left[0\right]:=evalExample,[x=0]);\)
\(N\left[2\right]:=eval(Example,[x=2]);\)
\(N\left[4\right]:=eval(Example,[x=4]);\)
\(N\left[6\right]:=eval(Example,[x=6]);\)
\(N\left[8\right]:=eval(Example,[x=8]);\)
\(N\left[10\right]:=eval(Example,[x=10]);\)
end do
Step 7:
\(\psi\left[3Dplot\right]:=plot3d(Example,t=-\pi...\pi,x=-\pi...\pi,grid=[100,100],color);\)
\(\psi\left[2Dplot\right]:=plot([N[0],N[2],N[4],N[6],N[8],N[10]]),t=0...40,color\)
=[red,blue,green,yellow,black,purple],axes=BOXED,title=GDPDE);
\(\psi\left[2Dlogplot\right]:=logplot([N[0],N[2],N[4],N[6],N[8],N[10]]),t=0...40,color\)
=[red,blue,green,yellow,black,purple],axes=BOXED,title=GDPDE);
\(\psi\left[Densityplot\right]:=(Example,t=-100...100,x=0...-10);\)
Output: See analytic-numeric solutions (15,19,23),Tables 1-3 and Figures 1(a), 1(b), 1(c), 1(d),..., Figures 4(a), 4(b), 4(c), where is the computational length and is a positive constant.
3. Numerical examples
Example 1. Consider the nonlinear nonhomogeneous gas dynamic equation [2,3,4,7,10,15]
The numerical solutions for Example 1 is given in Table 1.
Table 1. Numerical solutions \(\psi(x,t) at x=0.001\).
| \(\psi(x,t)\) | Solution | Example 1 |
|---|---|---|
| (0.001, 0.00) | Analytical | 0.00099950016662500833194464283234403 |
| MNIA | 0.00099950016662500833194464283234403 | |
| (0.001, 0.20) | Analytical | -0.2201819658998724994169694170106571 |
| MNIA | -0.2201819658998724994169694170106571 | |
| (0.001, 0.40) | Analytical | -0.4903336186074025654679095480461317 |
| MNIA | -0.4903336186074025654679095480461317 | |
| (0.001, 0.60) | Analytical | -0.8202975923459081008581182027221291 |
| MNIA | -0.8202975923459081008581182027221291 | |
| (0.001, 0.80) | Analytical | -1.2233164999636086074556190524624456 |
| MNIA | -1.2233164999636086074556190524624456 | |
| (0.001, 0.10) | Analytical | -1.7155649053185666873319827333452869 |
| MNIA | -1.7155649053185666873319827333452869 |
Example 2. Consider the nonlinear nonhomogeneous gas dynamic equation [2,3,4,7,10,15]
Table 2. Numerical solutions \(\psi(x,t) at x=0.001\).
| \(\psi(x,t)\) | Solution | Example 2 |
|---|---|---|
| (0.001, 0.00) | Analytical | 0.00099950016662500833194464283234403 |
| MNIA | 0.00099950016662500833194464283234403 | |
| (0.001, 0.20) | Analytical | -0.2201819658998724994169694170106571 |
| MNIA | -0.2201819658998724994169694170106571 | |
| (0.001, 0.40) | Analytical | -0.4903336186074025654679095480461317 |
| MNIA | -0.4903336186074025654679095480461317 | |
| (0.001, 0.60) | Analytical | -0.8202975923459081008581182027221291 |
| MNIA | -0.8202975923459081008581182027221291 | |
| (0.001, 0.80) | Analytical | -1.2233164999636086074556190524624456 |
| MNIA | -1.2233164999636086074556190524624456 | |
| (0.001, 0.10) | Analytical | - 1.7155649053185666873319827333452869 |
| MNIA | -1.7155649053185666873319827333452869 |
Compare and apply Eq. (14) with Algorithm 1, when \(N=2\), \(\tau=1\), \(g\left(x,t\right)=-e^{t-x}\) and \(h\left(x\right)=1-e^{-x}\). We obtain approximate solution as follow:
Example 3. Consider the nonlinear homogenous gas dynamic equation [2,3,4,7,10,15]
The numerical solutions for Example 3 is given in Table 3.
Table 3. Numerical solutions \(\psi(x,t) at x=0.001\).
| \(\psi(x,t)\) | Solution | Example 3 |
|---|---|---|
| (0.001, 0.00) | Analytical | 0.99900049983337499166805535716765597 |
| MNIA | 0.99900049983337499166805535716765597 | |
| (0.001, 0.20) | Analytical | 1.22018196589987249941696941701065712 |
| MNIA | 1.22018196589987249941696941328796801 | |
| (0.001, 0.40) | Analytical | 1.49033361860740256546790954804613177 |
| MNIA | 1.49033361860740256546741607307804137 | |
| (0.001, 0.60) | Analytical | 1.82029759234590810085811820272212919 |
| MNIA | 1.82029759234590810036634516523928928 | |
| (0.001, 0.80) | Analytical | 2.22331649996360860745561905246244569 |
| MNIA | 2.22331649996360854127633798922881128 | |
| (0.001, 0.10) | Analytical | 2.71556490531856668733198273334528698 |
| MNIA | 2.71556490531856371400530255152074189 |
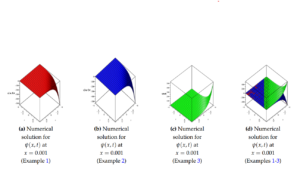
Figure 1. Depict 3D plot numerical solutions and multiple 3D plots for gas flow for Example 1, Example 2 and Example 3.
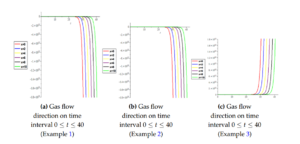
Figure 2. Depict 2D plot numerical solutions for gas flow on time interval \(0\le t \le40\) Example 1, Example 2 and Example 3.
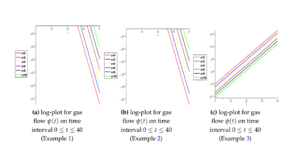
Figure 3. Depict 2D log-plot numerical solutions for gas flow on time interval \(0\le t \le40\) Example 1, Example 2 and Example 3.
4. Conclusion
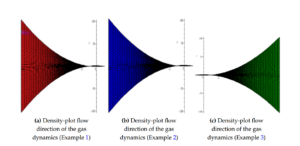
In this paper, the modified new iterative algorithm (MNIA) was formulated and applied to obtain analytic-numeric solutions to the homogeneous and nonhomogeneous nonlinear gas-dynamics equation. The proposed algorithm gave analytic-numeric solutions of the three examples considered with high accuracy and good agreement with analytical solutions. The Figures 1(a), 1(b), 1(c), 1(d) depicts numerical solutions on a 3Dplot pertain to gas dynamics flow in fluid mechanics and thermodynamics, Figures 2(a), 2(b), 2(c) depict the 2D plot of gas flow in a given time interval, while 2D Logarithm-plots are presented in Figures 3(a), 3(b), 3(c) and Figures 4(a), 4(b), 4(c) demonstrated the density-plots direction of the gas flow in a gas chamber. Moreover, from the computational point of view, the proposed algorithm is faster in convergence rate, powerful and efficient in finding analytical and approximate solutions for similar nonlinear differential equations arising in applied sciences and engineering.
Figure 4. Demonstrate the density-plot profile direction of gas dynamics flow Example 1, Example 2 and Example 3.
Conflicts of Interest:
''The author declares no conflict of interest.''References
- Aminikhah, H., & Jamalian, A. (2013). Numerical approximation for nonlinear gas dynamic equation. International Journal of Partial Differential Equations, 2013, Article ID 846749. https://doi.org/10.1155/2013/846749. [Google Scholor]
- Nikkar, A. (2012). A new approach for solving gas dynamic equation. Acta Technica Corviniensis-Bullettin of Engineering, Tome V Fascicule 4, 1-4. [Google Scholor]
- Hossein, J., Changbum C., Seifi, S., & Saeidy, M. (2009). Analytical solution for nonlinear Gas dynamic equation by homotopy analysis method. Applications and Applied Mathematics: An International Journal, 4(1), 149- 154.[Google Scholor]
- Adesina, K. A. (2017). A reliable technique for solving gas dynamic equation using natural homotopy perturbation method. Global Journal of Science Frontier Research: F Mathematics and Decision Sciences, 17(6), 1-9. [Google Scholor]
- Shehu, M., & Sabuwa, M.K. (2014). An efficient technique for solving Gas dynamics equation using the natural decomposition method. International Mathematical Forum, 9(24), 1177 - 1190. [Google Scholor]
- PremKiran, G. B., & Pradhan, V. H. (2013). Elzaki transform homotopy perturbation method for solving gas dynamics equation. International Journal of Research in Engineering and Technology, 2(12), 260-264. [Google Scholor]
- Evans, D. J. & Bulut, H. (2002). A new approach to the gas dynamics equation: an application of the decomposition method. International Journal of Computer Mathematics, 79(7), 817-822. [Google Scholor]
- Rasulov, M., & Karaguler,T. (2003).Finite difference schemes for solving system equations of gas dynamic in a class of discontinuous functions. Applied Mathematics and Computation, 143(1), 145-164. [Google Scholor]
- Mohiuddin, G. (2015). Modified homotopy perturbation method (MHPM) for dynamics gas equation. Mathematical Theory and Modelling, 5(6), 173-175. [Google Scholor]
- Joseph, B. Y., Stevy, M. M. & Gabriel, B. (2020). Application of Laplace variation iteration method to solving the nonlinear Gas dynamics equation. American Journal of Mathematical and Computer Modelling, 5(4), 127-133. [Google Scholor]
- Daftardar-Gejji, V., & Jafari, H. (2006). Solving a system of nonlinear equations using new iterative method. Journal of Mathematics Analysis and Application. 316, 753-763. [Google Scholor]
- Bhalekar, S., & Daftardar-Gejji, V. (2008). New iterative method: application to partial differential equations. Applied Mathematics and Computation, 203(2), 778-783. [Google Scholor]
- Zead, Y., & Ali, A. (2018). Application new iterative method for solving nonlinear Burger' s equation and coupled Burger's equations. IJCSI International Journal of Computer Science, 15(3), 31-35. [Google Scholor]
- Yaseen, M., & Samraiz, M. (2012). The modified new iterative method for solving linear and nonlinear Klein-Gordon equations. Applied Mathematical Sciences, 6(60), 2979-2987. [Google Scholor]
- Elzaki, S. M. (2014). Exact solution of nonlinear gas dynamic equation using projected differential transform method. International Journal of Innovation in Science and Mathematics, 2(5), 442-444. [Google Scholor]
Appendix: Maple 18 software code for MNIA Example 1
Algorithm 2. with(plots);
animate, animate3d, animatecurve, arrow, changecoords, complexplot, complexplot3d, conformal, conformal3d, contourplot, contourplot3d, coordplot, coordplot3d, densityplot, display, dualaxisplot, fieldplot, fieldplot3d, gradplot, gradplot3d, implicitplot, implicitplot3d, inequal, interactive, interactiveparams, intersectplot, listcontplot, listcontplot3d, listdensityplot, listplot, listplot3d, loglogplot, logplot, matrixplot, multiple, odeplot, pareto, plotcompare, pointplot, pointplot3d, polarplot, polygonplot, polygonplot3d, polyhedra\_supported, polyhedraplot, rootlocus, semilogplot, setcolors, setoptions, setoptions3d, spacecurve, sparsematrixplot, surfdata, textplot, textplot3d, tubeplot
restart; Digits:=35;
Digits:=35
N:=2;
N:=2
\(h:=1-e^{-x};\tau:=\frac{1}{2};g:=e^{t-x};\psi[0]:=h\)
\(h:=1-e^{-x}\)
\(\tau:=\frac{1}{2}\)
\(g:=e^{t-x}\)
\(\psi_{0}=1-e^{-x}\)
\(GDPDE:=value(-\tau\cdot Diff((\psi[0])^{2},x)+(\psi[0])\cdot(1-(\psi[0]))-g)\)
\(GDPDE:=-e^{t-x}\)
\(\psi[1]:=value(Int(GDPDE,t=0..t))\)
\(\psi_{1}:=e^{-x}-e^{t-x}\)
for m from 1 to N do\(\psi[m+1]:=value(Int(-\pi\cdot Diff(sum(\psi[n],n=0..m)^{2},x)+(sum(\psi[n],n=0..m))\cdot(1 -(sum(\psi[n],n=0..m)))-g,t-0..t)\)
\(-Int(-\tau\cdot Diff(sum(\psi[n],n=0..m-1)^{2},x) +(sum(\psi[n],n=0..m-1))\cdot(1-(sum(\psi[n],n=0..m-1)))-g,t=0..t))\)
end do\(\psi_2:=0\)
\(\psi_3:=0\)
\(Example[1]:=evalf(sum(\psi[k],k=0..N+1))\);
\(Example_1:=1.-1.e^{t-1.x}\)
for i from 0 by 0.2 to 1 do \(\psi[i]:=\)evalf(eval(Example[1],[x=0.001,t=i]));end do
\(\psi_0:=0.00099950016662500833194464283234403\)
\(\psi_{0.2}:=-0.2201819658998724994169694170106571\)
\(\psi_{0.4}:=-0.4903336186074025654679095480461317\)
\(\psi_{0.6}:=-0.8202975923459081008581182027221291\)
\(\psi_{0.8}:=-1.2233164999636086074556190524624456\)
\(\psi_{1.0}:=-1.7155649053185666873319827333452869\)
\(N[0]:=eval(Example[1],x=0);\)
\(N[1]:=eval(Example[1],x=2);\)
\(N[2]:=eval(Example[1],x=4);\)
\(N[3]:=eval(Example[1],x=6);\)
\(N[4]:=eval(Example[1],x=8);\)
\(N[5]:=eval(Example[1],x=10);\)
\(N_0:=1.-1.e^{t}\)
\(N_1:=1.-1.e^{t-2}\)
\(N_2:=1.-1.e^{t-4}\)
\(N_3:=1.-1.e^{t-6}\)
\(N_4:=1.-1.e^{t-8}\)
\(N_5:=1.-1.e^{t-10}\)
plot3d(Example[1],x=-Pi..Pi,t=-Pi..Pi,grid=[100,100],color="red")
plot([N[0],N[1],N[2],N[3],N[4],N[5]],t=0..40,color=[red,blue,yellow,purple, black,green],axes=BOXED,title="Example 1 GDPDE")
logplot([N[0],N[1],N[2],N[3],N[4],N[5]],t=0..40,color=[red,blue,yellow,purple, black,green],axes=BOXED,title="Example 1 GDPDE")
densityplot(Example1,x=0,t=-100..100,colorstyle=red;