Open Journal of Discrete Applied Mathematics
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2022.0074
KG-Sombor index of Kragujevac trees
Ivan Gutman\(^{1,*}\), Izudin Redžepović\(^1\) and Veerabhadrappa R. Kulli\(^{2}\)
\(^{1}\) Faculty of Science, University of Kragujevac, 34000 Kragujevac, Serbia.
\(^{2}\) Department of Mathematics, Gulbarga University, Kalaburgi 585 106, India.
Correspondence should be addressed to Ivan Gutman at gutman@kg.ac.rs
Abstract
Keywords:
1. Introduction
Let \(G\) be a simple graph, with vertex set \(\mathbf V(G)\) and edge set \(\mathbf E(G)\). Then \(|\mathbf V(G)|\) and \(|\mathbf E(G)|\) are the number of vertices and edges of \(G\). By \(e=uv \in \mathbf E(G)\) we denote the edge of \(G\), connecting the vertices \(u\) and \(v\). The degree of a vertex \(u \in \mathbf V(G)\) (= number of vertices that are adjacent to \(u\)) is denoted by \(d(u)\). The degree of an edge \(e \in \mathbf E(G)\) (= number of edges that are incident to \(e\)) is denoted by \(d(e)\). Recall that if \(e=uv\), then \(d(e)=d(u)+d(v)-2\).
For other graph-theoretical notions, the readers are referred to textbooks [1,2,3].
In the mathematical and chemical literature, some fifty or more different vertex-degree-based graph invariants (topological indices) have been defined and examined, all of the form
The oldest such invariant, conceived as early as in the 1970s, is the first Zagreb index, \(Zg\) [4]. One of the newest such invariant is the Sombor index, \(SO\) [5,6]. These are defined as
Recently a vertex-edge variant of the Sombor index was introduced [16,17], defined as
By continuing the considerations from Ref. [27], we now focus our attention to the KG-Sombor index. In order that the present article be self-contained, we repeat the definition of Kragujevac trees (as slightly modified in [27]).
2. Preparations
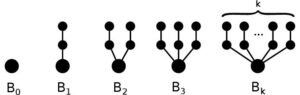
Let \(n\) be a positive integer. For \(k=0,1,\ldots,n\), we denote by \(B_k\) the rooted tree with \(2k+1\) vertices, constructed by attaching \(k\) two-vertex branches to the root, see Figure 1.
Figure 1. Rooted trees \(B_0\), \(B_1\), \(B_2\), \(B_3\), and \(B_k\). Their roots are indicated by large dots.
Let \(k_i\,,\,i=1,2,\ldots,n\), be non-negative integers, such that
Definition 1. Let the parameters \(k_1,k_2,...,k_n\) satisfy the condition (6). Then the Kragujevac tree \(Kg(k_1,k_2,\ldots,k_n)\) is the tree obtained from \(B_{k_1}\), \(B_{k_2}\), \(\ldots\) \(B_{k_n}\), by connecting their roots to a new vertex.
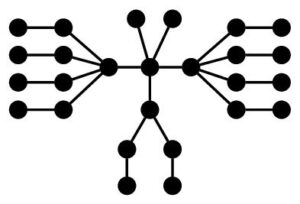
In Figure 2 an example is depicted, illustrating Definition 1.
Figure 2. The Kragujevac tree \(Kg(0,0,2,4,4)\), for which \(n=5\) and \(K=10\). Note that there exist 30 mutually non-isomorphic Kragujevac trees with parameters \(n=5\) and \(K=10\).
According to Definition 1, the Kragujevac tree with parameters \(k_1,k_2,\ldots,k_n\) has
\[ 1 + \sum_{i=1}^n (2\,k_i + 1) = 2K + n + 1 \] vertices.An edge connecting a vertex of degree \(i\) and a vertex of degree \(j\) will be referred to as an \((i,j)\)-edge. Directly from Definition 1 we obtain:
Proposition 2. Let \(Kg(k_1,k_2,\ldots,k_n)\) be a Kragujevac tree. Then it has \(K\) \((1,2)\)-edges, \(k_i\) \((k_i+1,2)\)-edges for each \(i=1,2,\ldots,n\), and a \((k_i+1,n)\)-edge for each \(i=1,2,\ldots,n\).
Applying Proposition 2 to Eq. (5) we arrive at:Lemma 3. The KG-Sombor index of the Kragujevac tree \(Kg(k_1,k_2,\ldots,k_n)\) depends on its structural parameters as
3. Main results
In this section, we determine the extremal Kragujevac trees (minimal and maximal) concerning the KG-Sombor index. In order to achieve this goal, we first recall a similar result established for the first Zagreb index, [27].Lemma 4. Let \(Kg = Kg(k_1,k_2,\ldots,k_n)\) be the Kragujevac tree whose parameters satisfy Eqs. (6) and (7). Then \(Zg(Kg)\) is minimal if and only if \[ k_i \in \left\{ \left\lfloor \frac{K}{n} \right\rfloor, \left\lceil \frac{K}{n} \right\rceil \right\} \ \ \mbox{for} \ \ i=1,2,\ldots, n, \hspace{10mm} \mbox{i.e.,} \hspace{10mm} k_n - k_1 \leq 1\,. \] and \(Zg(Kg)\) is maximal if and only if \[ k_1=k_2= \cdots = k_{n-1}=0 \hspace{10mm} \mbox{and} \hspace{10mm} k_n=K\,. \]
In order to use the results of Lemma 4, we need to establish a relation between the first Zagreb and the KG-Sombor indices. This is achieved using the following simple argument. Note that bounds analogous to (10) were previously obtained for the ordinary Sombor index, Eq. (3) [6].For any positive numbers \(a\) and \(b\),
Lemma 5. For any graph \(G\) with \(m\) edges,
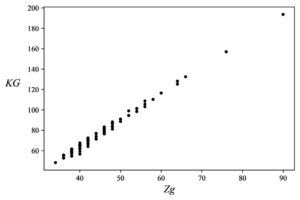
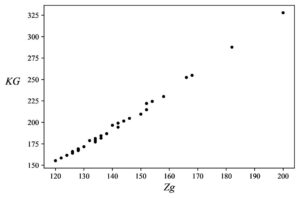
Inequalities (10) indicate that the KG-Sombor and first Zagreb indices should be linearly correlated. Indeed, in the case of trees (with a fixed number of vertices) this correlation was found to be remarkably good, see Figures 3 and 4, and Table 1.
Figure 1. KG-Sombor indices (\(KG\)) of 10-vertex trees, plotted versus the respective first Zagreb indices (\(Zg\)), cf. Table 1.
Table 1. The parameters of the regression line \(KG=a\,Zg + b\) for \(N\)-vertex trees; \(R\) = correlation coefficient.
| \(N\) | \(a\) | \(b\) | \(R\) |
|---|---|---|---|
| 10 | \(2.61 \pm 0.03\) | \(-40.27 \pm 1.15\) | 0.9952 |
| 11 | \(2.60 \pm 0.02\) | \(-44.94 \pm 0.89\) | 0.9947 |
| 12 | \(2.58 \pm 0.01\) | \(-49.13 \pm 0.64\) | 0.9946 |
| 13 | \(2.58 \pm 0.01\) | \(-53.71 \pm 0.47\) | 0.9942 |
| 14 | \(2.57 \pm 0.01\) | \(-58.13 \pm 0.34\) | 0.9940 |
| 15 | \(2.57 \pm 0.03\) | \(-62.69 \pm 0.24\) | 0.9937 |
Figure 4. KG-Sombor indices (\(KG\)) of Kragujevac trees with parameters \(n=5\) and \(K=10\), plotted versus the respective first Zagreb indices (\(Zg\)); cf. caption of Figure 2.
Bearing these numerical results in mind, we maintain to be justified to state the following analogue of Lemma 4:
Proposition 6. Let \(Kg = Kg(k_1,k_2,\ldots,k_n)\) be the Kragujevac tree whose parameters satisfy Eqs. (6) and (7). Then \(KG(Kg)\) is minimal if and only if \[ k_i \in \left\{ \left\lfloor \frac{K}{n} \right\rfloor, \left\lceil \frac{K}{n} \right\rceil \right\} \ \ \mbox{for} \ \ i=1,2,\ldots, n, \hspace{10mm} \mbox{i.e.,} \hspace{10mm} k_n - k_1 \leq 1\,. \] and \(KG(Kg)\) is maximal if and only if \[ k_1=k_2= \cdots = k_{n-1}=0 \hspace{10mm} \mbox{and} \hspace{10mm} k_n=K\,. \]
A somewhat stronger claim, based on the numerical results presented in Figure 4, would be:Proposition 7. Let \(Kg_a\) and \(Kg_b\) be two Kragujevac trees with equal \(n\) and \(K\) values. Then \[ Zg(Kg_a) > Zg(Kg_b) \ \Leftrightarrow \ KG(Kg_a) > KG(Kg_b)\,. \]
Assuming that Proposition 6 is valid, we have the following results:If \(Kg\) is a Kragujevac tree with parameters \(n\) and \(K\), then the maximum value of \(KG(Kg)\) is
\begin{eqnarray*} && (\sqrt{8}+\sqrt{5})K + \sqrt{2}\,K^2 + K\,\sqrt{K^2+2K+5} + \sqrt{2K^2+n^2+2nK-2n+2} +\, \sqrt{K^2+2Kn-2K+2n^2-2n+1}\,. \end{eqnarray*} The minimum value of \(KG(Kg)\) depends on the parameter \(p\), defined via \(K \equiv p\,(\hspace{-3mm} \mod n)\). For instance, for \(p=0\), this minimum value is \begin{eqnarray*} && (\sqrt{8}+\sqrt{5})K + \sqrt{2}\,K\,x + K\,\sqrt{x^2+2x+5} + n\,\sqrt{2x^2+n^2+2nx-2n+2} + \, n\,\sqrt{x^2+2nx-2x+2n^2-2n+1}\,, \end{eqnarray*} where \(x=K/n\).4. Concluding remarks
Recently, the first Banhatti (a,b)-KA index of a graph was defined as [17] \[ BKA^1_{a,b}(G) = \sum_{ue} \Big[ d(u)^a + d(e)^a \Big]^b\,. \] We quickly see that \(BKA^1_{1,1}\) is the ordinary first Bahnatti index [28], whereas \(BKA^1_{2,1/2}\) is the KG-Sombor index. Thus, studying the \(BKA^1_{a,b}\)-index and its extremal values will be challenging.In this paper, a combinatorial expression, Eq. (5), is established for the KG-Sombor index of Kragujevac trees. Because of the perplexing form of formula (5), our approach towards finding the extremal values of \(KG(Kg)\), Proposition 6, used the analogous results earlier established for the first Zagreb index (Lemma 4), combined with Lemma 5, and the fact that there exists an excellent linear correlation between KG-Sombor and first Zagreb indices. This latter fact was empirically verified for both general and Kragujevac trees, see Figs. 3 and 4. Finding a rigorous analytical proof of our Propositions 6 and 7 remains a challenge for the future but appears to be a prohibitively tricky task.
Comparing Eqs. (3) Furthermore, (4), it is obvious why ''Sombor'' is used in the name of the KG-index. At this point, we reveal that ''KG'' indicates the names of the inventors of this index - V. R. K & I. G.
Author Contributions:
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflicts of Interest:
''The authors declare no conflict of interest.''Acknowledgments :
Izudin Redžepovic was supported by the Serbian Ministry of Education, Science and Technological Development (Grant No. 451-03-68/2022-14/200122).References
- Bondy, J. A., & Murty, U. S. R. (1976). Graph Theory with Applications. New York: Macmillan Press. [Google Scholor]
- Kulli, V. R. (2012). College Graph Theory. Gulbarga: Vishwa International Publications. [Google Scholor]
- Wagner, S., & Wang, H. (2018). Introduction to Chemical Graph Theory. Boca Raton: CRC Press. [Google Scholor]
- Gutman, I., & Trinajstic, N. (1972). Graph theory and molecular orbitals. Total \(\pi\)-electron energy of alternant hydrocarbons. Chemical Physics Letters, 17, 535-538. [Google Scholor]
- Gutman, I. (2021). Geometric approach to degree-based topological indices: Sombor indices. MATCH Communications in Mathematical and in Computer Chemistry, 86, 11-16. [Google Scholor]
- Gutman, I. (2021). Some basic properties of Sombor indices. Open Journal of Discrete Appllied Mathematics, 4(1), 1-3. [Google Scholor]
- Das, K. C., Çevik, A. S., Cangul, I. N., & Shang, Y. (2021). On Sombor index. Symmetry. 13, Article No. 140, https://doi.org/10.3390/sym13010140. [Google Scholor]
- Kulli, V. R. (2021). Sombor index of certain graph operators. International Journal of Engineering Sciences & Research Technology, 10, 127-134. [Google Scholor]
- Liu, H., Gutman, I., You, L., & Huang, Y. (2022). Sombor index: Review of extremal results and bounds. Journal of Mathematical Chemistry, 66, 771-798. [Google Scholor]
- Rada, J., Rodríguez, J. M., & Sigarreta, J. M. (2021). General properties of Sombor indices. Discrete Applied Mathematics, 299, 87-97. [Google Scholor]
- Shang, Y. (2022). Sombor index and degree-related properties of simplicial networks. Applied Mathematics and Computation, 419, Article No. 126881, https://doi.org/10.1016/j.amc.2021.126881. [Google Scholor]
- Wang, F., Wu, B. (2022). The reduced Sombor index and the exponential reduced Sombor index of a molecular tree. Journal of Mathematical Analysis and Applications, 515(2), Article No. 126442, https://doi.org/10.1016/j.jmaa.2022.126442. [Google Scholor]
- Redžepovic,, I. (2021). Chemical applicability of Sombor indices. Journal of the Serbian Chemical Society, 86, 445-457. [Google Scholor]
- Amin, S., Rehman, M. A., Naseem, A., Younis, J., & Asghar, S. S. (2022). Analysis of bismuth (III) iodide and dendrimers in drug applications. Journal of Chemistry, 2022, Article ID 3163294, https://doi.org/10.1155/2022/3163294. [Google Scholor]
- Asif, F., Zahid, Z., Husin, M. N., Cancan, M., Tas, Z., Alaeiyan, M., & Farahani, M. R. (2022). On Sombor indices of line graph of silicate carbide \(Si_2C_3-I[p,q]\). Journal of Discrete Mathematical Sciences and Cryptography, 25, 301-310. [Google Scholor]
- Kulli, V. R., Harish, N., Chaluvaraju, B., & Gutman, G. (2022). Mathematical properties of KG Sombor index. Bulletin of International Mathematical Virtual Institute, 12, 379-386. [Google Scholor]
- Kulli, V. R. (2022). KG Sombor indices of certain chemical drugs. International Journal of Engineering Sciences & Research Technology, 11(6), 27-35. [Google Scholor]
- Hosseini, S. A., Ahmadi, M. B., & Gutman, I. (2014). Kragujevac trees with minimal atom-bond connectivity index. MATCH Communications in Mathematical and in Computer Chemistry, 71, 5-20. [Google Scholor]
- Ali, A., Das, K. C., Dimitrov, D., & Furtula, B. (2021). Atom-bond connectivity index of graphs: A review over extremal results and bounds. Discrete Mathematics Letters, 5, 68-93. [Google Scholor]
- Basavanagoud, B., & Timmanaikar, S. (2017). Computing first Zagreb and forgotten indices of certain dominating transformation graphs of Kragujevac trees. Journal of Computational Mathematical Science, 8(3), 50-61. [Google Scholor]
- Cruz, R., Gutman, I., & Rada, J. (2014). Topological indices of Kragujevac trees. Proyecciones Journal of Mathematics, 33, 471-482. [Google Scholor]
- Gutman, I. (2014). Kragujevac trees and their energy. Scientific Publications of the State University Novi Pazar, 6, 71-79. [Google Scholor]
- Mirajkar, K. G., Doddamani, B. R., & Priyanka, Y. B. (2017). Atom bond connectivity indices of Kragujevac trees. International Journal of Currenat Research Review, 9(15), 1-7. [Google Scholor]
- Rezaei, M., Hosamani, S. M., Farahani, M. R., & Jamil, M. K. (2017). On the terminal Wiener index and Zagreb indices of Kragujevac trees, International Journal of Pure and Applied Mathematics, 113, 617-625. [Google Scholor]
- Shirkol, S. S., Hosamani, S. M., & Patil, S. V. (2017). Acharya polynomial of some graph transformations. Bulletin of Mathematical and Statistical Research, 5, 75-83. [Google Scholor]
- Kanwal, S., Safdar, R., Rauf, A., Afzal, A., Jamshed, W., Alanazi, M. M., & Zahran, H. Y. (2022). On chemical invariants of semitotal-point graph and its line structure of the acyclic Kragujevac network: A novel mathematical analysis. Journal of Chemistry, 2022, Article ID 7995704, https://doi.org/10.1155/2022/7995704. [Google Scholor]
- Gutman, I., Kulli, V. R., & Redžepovic, I. (2021). Sombor index of Kragujevac trees, Scientific Publications of the State University Novi Pazar, 13, 61-70. [Google Scholor]
- Kulli, V. R. (2016). On K Banhatti indices of graphs. Journal of Computer and Mathematical Sciences, 7(4), 213-218 [Google Scholor]