Open Journal of Mathematical Analysis
ISSN: 2616-8111 (Online) 2616-8103 (Print)
DOI: 10.30538/psrp-oma2022.0113
Solution of generalized Abel’s integral equation using orthogonal polynomials
Mamman Ojima John\(^{1,*}\), Aboiyar Terhemen\(^{1}\) and Tivde Tertsegha\(^1\)
\(^1\) Department of Mathematics/Statistics/Computer Science, Faculty of Science, Federal University of Agriculture Makurdi, Benue State, Nigeria.
Correspondence should be addressed to Mamman Ojima John at mammanojima@gmail.com
Abstract
Keywords:
1. Introduction
Fractional calculus is a branch of mathematical analysis that investigates integrals and derivatives of fractional real and complex order with their applications. Abel's integral equation was investigated and developed by Niels Henrik Abel when he was solving and generalizing the Tautochrone problem. It enables users to compute the total time required for a particle to fall along a given curve [1]. Abel integral equations have been generalized through the theory of fractional integral equations.
Recent times, literature shows large number of engineering and scientific research involving fractional order calculus (foc), the simple reason is that it provides an accurate models of systems being considered [2]. The history [3] which is well established that several real life phenomena can not find adequate representation in the regular integer order calculus but are better described by fractional order calculus, with this, several approaches have been adopted to solve Abel's integral equations [4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19] which he generalized. Progress [20, 21] however has been made with respect to interpretation of non-integer order integral and derivative. Several numerical methods [4, 5, 7, 8, 10] for the solutions of this integral equation have been developed such as solutions in Distribution, Banach Spaces and a host of others with applications which are commonly found in modeling the dynamics of interfaces between nanoparticles and substrates [22], oscillation [23], signal processing [24], frequency dependent damping behavior of many viscoelastic materials [25], continuum and statistical mechanics [26], and economics [27].
The ideas of fractional integral operators to solve a system of generalized Abel integral equations can be found in [28], numerous attempts to solve Abel's equations involving different types of operators can be found in the literature.
2. Materials and methods
This section, presents some definitions and mathematical preliminaries which are necessary for the evaluation of the fractional calculus [30] which will be used in this paper. The Riemann--Liouville fractional integral of order \(\alpha\) can be defined mathematically as:Proposition 1.[29] For \(J^{\alpha }\), the following properties holds, \(u_{i} \in c_{\mu}\), \(i=0\dots n,\) \(\mu\ge -1\) is defined as:
- \(J^{\alpha }\left(\sum\limits^n_{i=0}{u_i\left(x\right)}\right)=\sum\limits^n_{i=0}{J^{\alpha }u_i\left(x\right)},\)
- \(J^{\alpha }x^{\beta }=\frac{\Gamma(\beta +1)}{\Gamma(\alpha +\beta +1)}x^{\alpha +\beta }, \beta \ >\ -1.\)
2.1. Legendre polynomials
The following isLegendre's differential equation in mathematics,2.2. Chebyshev polynomials
Pafnuty Chebyshev introduced Chebyshev polynomials, which was named after him are a sequence of polynomials similar to the trigonometric multi-angle formulae. The Chebyshev differential equation is written as2.3. Hermite polynomials
The Hermite polynomials, named after Charles Hermite are solutions of Hermite equation,2.4. Abel's integral equations of the first kind
Here, we consider the use of Legendre, Chebyshev and Hermite series for solving Abel's integral equations. The derivation of the method for the first kind is given below: Considering Eqs \eqref{GrindEQ__1_} and \eqref{GrindEQ__4_}, we have2.5. Abel's integral equations of the second kind
In a similar fashion, we derive for the second kind as follows: We can rewrite \eqref{GrindEQ__5_} by considering \eqref{GrindEQ__1_} as3. Results and discussion
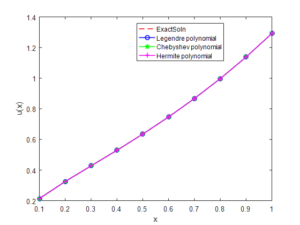
Example 1. The Abel's integral equation of the first kind is \[\int^x_0{\frac{u(t)}{\sqrt{(x-t)}}dt}=e^x-1\,,\] with exact solution \(\frac{1}{\sqrt{}\pi }e^x{\mathrm{erf} \left(\sqrt{x}\right)\ },\) where \({\mathrm{erf} \left(x\right)\ }\) is error function defined by \[{\mathrm{erf} \left(x\right)\ }=\frac{2}{\sqrt{\pi }}\int^x_0{e^{-{\varphi }^2d\varphi }}.\] From Eq. \eqref{GrindEQ__26_}, we have \[f\left(x\right)=\Gamma\left(1-\alpha \right)\left(\sum^n_{i=0}{a_iJ^{1-\alpha }}{\phi }_i\left(x\right)\right)\,.\] Here \({\phi }_i\left(x\right)\) is the Legendre, Chebyshev or Hermite polynomials of degree \(i\) as defined in \eqref{GrindEQ__18_} and \eqref{GrindEQ__19_}, we can solve for each polynomial by expressing them in terms of their recurrence relation defined earlier. With the aid of MAPLE 17 we have our numerical solution in Tables 1 and 2.
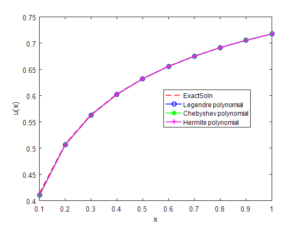
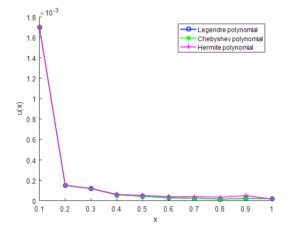
Example 2. The Abel's integral equation of second kind is, \[U\left(x\right)=2\sqrt{x}-\int^x_0{\frac{u\left(t\right)}{\sqrt{\left(x-t\right)}}dt}\,.\] The exact solution is \(1-e^{\pi x}erfc(\sqrt{\pi x})\), where \(erfc(\sqrt{\pi x})\) is a complementary error function defined as \[erfc\left(x\right)=\frac{2}{\sqrt{\pi }}\int^{\infty }_x{e^{-{\varphi }^2d\varphi }}.\] From Eq. \eqref{GrindEQ__28_} \[\sum^n_{i=0}{a_i\{}{\phi }_i\left(x\right)-\Gamma\left(1-\alpha \right)\sum^n_{i=0}{J^{1-\alpha }{\phi }_i\left(x\right)}\}=f\left(x\right)\,.\] The numerical results for this example are presented in Tables 3 and 4.
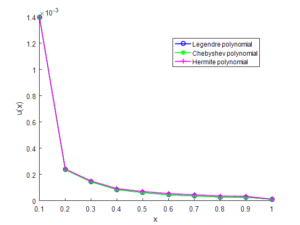
Table 1. Approximate solution, absolute errors and exact values of Example 1 for \(n=10\).
| \(\boldsymbol{x}\) (step size) | Exact Value | Legendre Polynomial | Abs. Error | Chebyshev Polynomial | Abs. Error |
|---|---|---|---|---|---|
| 0.1 | 0.2152905021 | 0.2139150700 | 0.0014 | 0.2139151530 | 0.0014 |
| 0.2 | 0.3258840762 | 0.3256471202 | 2.3696\(\times {10}^{-4}\) | 0.3256472151 | 2.3686\(\times {10}^{-4}\) |
| 0.3 | 0.4275656577 | 0.4274217109 | 1.4395\(\times {10}^{-4}\) | 0.4274218095 | 1.4385\(\times {10}^{-4}\) |
| 0.4 | 0.5293330732 | 0.5292480324 | 8.5041\(\times {10}^{-5}\) | 0.5292481234 | 8.4950\(\times {10}^{-5}\) |
| 0.5 | 0.6350318720 | 0.6349698900 | 6.1982\(\times {10}^{-5}\) | 0.6349699660 | 6.1906\(\times {10}^{-5}\) |
| 0.6 | 0.7470401733 | 0.7469949317 | 4.5242\(\times {10}^{-5}\) | 0.7469949759 | 4.5197\(\times {10}^{-5}\) |
| 0.7 | 0.8671875858 | 0.8671507681 | 3.6818\(\times {10}^{-5}\) | 0.8671507891 | 3.6797\(\times {10}^{-5}\) |
| 0.8 | 0.9970893764 | 0.997061161 | 2.8215\(\times {10}^{-5}\) | 0.997061163 | 2.8213\(\times {10}^{-5}\) |
| 0.9 | 1.138298578 | 1.138271221 | 2.7357\(\times {10}^{-5}\) | 1.138271301 | 2.7277\(\times {10}^{-5}\) |
| 1.0 | 1.292388093 | 1.29237800 | 1.0093\(\times {10}^{-5}\) | 1.29237801 | 1.0083\(\times {10}^{-5}\) |
Table 2. Approximate solution, absolute errors and exact values of Example 1 for \(n=10\).
| \(\boldsymbol{x}\)(step size) | \textbf{Exact Value} | \textbf{Hermite Polynomial} | \textbf{Abs. Error} |
|---|---|---|---|
| 0.1 | 0.2152905021 | 0.2139107224 | 0.0014 |
| 0.2 | 0.3258840762 | 0.3256418254 | 2.4225\(\times {10}^{-4}\) |
| 0.3 | 0.4275656577 | 0.4274153293 | 1.5033\(\times {10}^{-4}\) |
| 0.4 | 0.5293330732 | 0.5292405512 | 9.2522\(\times {10}^{-5}\) |
| 0.5 | 0.6350318720 | 0.6349614560 | 7.0416\(\times {10}^{-5}\) |
| 0.6 | 0.7470401733 | 0.7469858896 | 5.4284\(\times {10}^{-5}\) |
| 0.7 | 0.8671875858 | 0.8671416940 | 4.5892\(\times {10}^{-5}\) |
| 0.8 | 0.9970893764 | 0.9970529248 | 3.6452\(\times {10}^{-5}\) |
| 0.9 | 1.138298578 | 1.138264975 | 3.3603\(\times {10}^{-5}\) |
| 1.0 | 1.292388093 | 1.292375400 | 1.2693\(\times {10}^{-5}\) |
Table 3. Approximate solution, absolute errors and exact values of Example 2 for \(n=10\).
| \(\boldsymbol{x}\)(step size) | Exact Value | Legendre Polynomial | Abs. Error | Chebyshev Polynomial | Abs. Error |
|---|---|---|---|---|---|
| 0.1 | 0.4140591693 | 0.4102961743 | 0.0038 | 0.4102960583 | 0.0038 |
| 0.2 | 0.5083515180 | 0.5066321249 | 0.0017 | 0.5066320640 | 0.0017 |
| 0.3 | 0.5643086686 | 0.5631930727 | 0.0011 | 0.5631930909 | 0.0011 |
| 0.4 | 0.6033472169 | 0.6025423305 | 8.0489\(\times {10}^{-4}\) | 0.6025424464 | 8.0477\(\times {10}^{-4}\) |
| 0.5 | 0.6328679763 | 0.6322458378 | 6.2214\(\times {10}^{-4}\) | 0.6322460625 | 6.2191\(\times {10}^{-4}\) |
| 0.6 | 0.6563234564 | 0.6558226175 | 5.0084\(\times {10}^{-4}\) | 0.6558229644 | 5.0049\(\times {10}^{-4}\) |
| 0.7 | 0.6756010623 | 0.6751849583 | 4.1610\(\times {10}^{-4}\) | 0.6751854239 | 4.1564\(\times {10}^{-4}\) |
| 0.8 | 0.6918419681 | 0.691489126 | 3.5284\(\times {10}^{-4}\) | 0.6914896144 | 3.5235\(\times {10}^{-4}\) |
| 0.9 | 0.7057865180 | 0.705480729 | 3.0579\(\times {10}^{-4}\) | 0.7054813344 | 3.0518\(\times {10}^{-4}\) |
| 1.0 | 0.7179408238 | 0.71767526 | 2.6556\(\times {10}^{-4}\) | 0.7176760000 | 2.6482\(\times {10}^{-4}\) |
Table 4. Approximate solution, absolute errors and exact values of Example 2 for \(n=10\).
| \(\boldsymbol{x}\)(step size) | Exact Value | Hermite Polynomial | Abs. Error |
|---|---|---|---|
| 0.1 | 0.4140591693 | 0.4103001204 | 0.0038 |
| 0.2 | 0.5083515180 | 0.5066359852 | 0.0017 |
| 0.3 | 0.5643086686 | 0.5631970712 | 0.0011 |
| 0.4 | 0.6033472169 | 0.6025466640 | 8.0055\(\times {10}^{-4}\) |
| 0.5 | 0.6328679763 | 0.6322506550 | 6.1732\(\times {10}^{-4}\) |
| 0.6 | 0.6563234564 | 0.6558280064 | 4.9545\(\times {10}^{-4}\) |
| 0.7 | 0.6756010623 | 0.6751909250 | 4.1014\(\times {10}^{-4}\) |
| 0.8 | 0.6918419681 | 0.6914954448 | 3.4652\(\times {10}^{-4}\) |
| 0.9 | 0.7057865180 | 0.7054873805 | 2.9914\(\times {10}^{-4}\) |
| 1.0 | 0.7179408238 | 0.7176818000 | 2.5902\(\times {10}^{-4}\) |
Figure 1. Numerical and exact solutions of generalized Abel’s integral equation of Example 1 with \(\alpha\) = 0.5.
Figure 2. Error for generalized Abel’s integral equation for Example 1 with \(\alpha \) = \(\frac{1}{2}\).
Figure 3. Numerical and exact solutions of generalized Abel’s integral equation of Example 2 with \(\alpha \) = \(\frac{1}{2}\).
Figure 4. Error for generalized Abel’s integral equation for Example 2 with \(\alpha \) = \(\frac{1}{2}\).
4. Conclusion
In this research work, we implemented a method which was based on the use of infinite series of orthogonal polynomials to approximate the solution of the generalized Abel's integral equation which was generalized with the aid of fractional calculus. Furthermore, we described the properties of Legendre, Chebyshev and Hermite polynomials. We discussed and illustrated the numerical solutions of generalized Abel's integral equations using orthogonal polynomials. The efficiency of using orthogonal polynomials was illustrated by solving several examples of Abel's integral equations. Orthogonal polynomials were successfully applied to solve Abel's equations of order \(0\ < \ \alpha \ < \ 1\). All ideas were illustrated to be efficient in applying the proposed technique to several examples of that order. We found that the method is accurate and efficient in finding numerical solutions for those equations. More-over, using orthogonal polynomials demonstrate excellent approximations in comparison with the exact solutions and with other methods and solvers through the applicable domain. In addition, the occurred errors between using orthogonal polynomials for those equations of that orders and the exact solutions are small.Acknowledgments
The authors would like to thank the referee for his/her valuable comments that resulted in the present improved version of the article.Conflicts of Interest:
''The author declares no conflict of interest.''References
- Podlubny, I., Magin, R. L., & Trymorush, I. (2017). Niels Henrik Abel and the birth of fractional calculus. Fractional Calculus and Applied Analysis, 20(5), 1068-1075.[Google Scholor]
- Mamman, J. O., & Aboiyar, T. (2020). A numerical calculation of arbitrary integrals of functions. Advanced Journal of Graduate Research, 7(1), 11-17.[Google Scholor]
- Machado, J. T., & Kiryakova, V. (2017). The chronicles of fractional calculus. Fractional Calculus and Applied Analysis, 20(2), 307-336.[Google Scholor]
- Zarei, E., & Noeiaghdam, S. (2018). Solving generalized Abel's integral equations of the first and second kinds via Taylor-collocation method. arXiv preprint arXiv:1804.08571.[Google Scholor]
- Li, C., Humphries, T., & Plowman, H. (2018). Solutions to Abel's integral equations in distributions. Axioms, 7(3), Article No. 66.[Google Scholor]
- Li, C., & Srivastava, H. M. (2021). Uniqueness of solutions of the generalized Abel integral equations in Banach spaces. Fractal and Fractional, 5(3), Article No. 105.[Google Scholor]
- Li, C., & Plowman, H. (2019). Solutions of the generalized Abel's integral equations of the second kind with variable coefficients. Axioms, 8(4), Article No. 137. [Google Scholor]
- Kaewnimit, K., Wannalookkhee, F., Nonlaopon, K., & Orankitjaroen, S. (2021). The solutions of some Riemann-Liouville fractional integral equations. Fractal and Fractional, 5(4), Article no. 154. [Google Scholor]
- Deutsch, M., Notea, A., & Pal, D. (1990). Inversion of Abel's integral equation and its application to NDT by X-ray radiography. NDT international, 23(1), 32-38.[Google Scholor]
- Chakrabarti, A., & George, A. J. (1994). A formula for the solution of general Abel integral equation. Applied Mathematics Letters, 7(2), 87-90.[Google Scholor]
- Hilfer, R., & Luchko, Y. (2019). Desiderata for fractional derivatives and integrals. Mathematics, 7(2), Article No. 149. [Google Scholor]
- Garrappa, R., Kaslik, E., & Popolizio, M. (2019). Evaluation of fractional integrals and derivatives of elementary functions: Overview and tutorial. Mathematics, 7(5), Article no. 407. [Google Scholor]
- Kiryakova, V. (2017, December). Use of fractional calculus to evaluate some improper integrals of special functions. In AIP Conference Proceedings (Vol. 1910, No. 1, p. 050012). AIP Publishing LLC.[Google Scholor]
- Agarwal, P. (2013). Fractional integration of the product of two multivariables H-function and a general class of polynomials. In Advances in Applied Mathematics and Approximation Theory (pp. 359-374). Springer, New York, NY.[Google Scholor] s
- Kochubei, A., & Luchko, Y. (Eds.). (2019). Basic Theory. Walter de Gruyter GmbH & Co KG.[Google Scholor]
- Tenreiro Machado, J. A., Kiryakova, V., Mainardi, F., & Momani, S. (2018). Fractional calculus's adventures in Wonderland (Round table held at ICFDA 2018). Fractional Calculus and Applied Analysis, 21(5), 1151-1155.[Google Scholor]
- Fawang, L., Mark M, M., Shaher, M., Nikolai N, L., Wen, C., & Om P, A. (2010). Fractional differential equations. International Journal of Differential Equations, 2010, Article ID 215856.[Google Scholor]
- Ghosh, U., Sarkar, S., & Das, S. (2015). Solution of system of linear fractional differential equations with modified derivative of Jumarie type. American Journal of Mathematical Analysis, 3(3), 72-84.[Google Scholor]
- Razzaghi, M. (2018). A numerical scheme for problems in fractional calculus. In ITM Web of Conferences (Vol. 20, p. 02001). EDP Sciences.[Google Scholor]
- E Tarasov, V., & S Tarasova, S. (2019). Probabilistic interpretation of Kober fractional integral of non-integer order. Progress in Fractional Differentiation & Applications, 5(1), 1-5.[Google Scholor]
- Podlubny, I. (2001). Geometric and physical interpretation of fractional integration and fractional differentiation. Fractional Calculus and Applied Analysis, 5(4), 367-386.[Google Scholor]
- Chow, T. S. (2005). Fractional dynamics of interfaces between soft-nanoparticles and rough substrates. Physics Letters A, 342(1-2), 148-155.[Google Scholor]
- Feng, Q. (2019). Oscillation for a class of fractional differential equation. Journal of Applied Mathematics and Physics, 7(7), 1429.[Google Scholor]
- Panda, R., & Dash, M. (2006). Fractional generalized splines and signal processing. Signal Processing, 86(9), 2340-2350.[Google Scholor]
- Bagley, R. L., & Torvik, P. J. (1983). A theoretical basis for the application of fractional calculus to viscoelasticity. Journal of Rheology, 27(3), 201-210.[Google Scholor]
- Mainardi, F. (1997). Fractional calculus. In Fractals and Fractional Calculus in Continuum Mechanics (pp. 291-348). Springer, Vienna.[Google Scholor]
- Baillie, R. T. (1996). Long memory processes and fractional integration in econometrics. Journal of Econometrics, 73(1), 5-59.[Google Scholor]
- Gong, C., Bao, W., Tang, G., Jiang, Y., & Liu, J. (2015). Computational challenge of fractional differential equations and the potential solutions: a survey. Mathematical Problems in Engineering, 2015, Article ID 258265. [Google Scholor]
- Avazzadeh, Z., Shafiee, B., & Loghmani, G. B. (2011). Fractional calculus for solving Abel's integral equations using Chebyshev polynomials. Applied Mathematical Sciences, 5(45), 2207-2216.[Google Scholor]
- Diethelm, K., Ford, N. J., & Freed, A. D. (2004). Detailed error analysis for a fractional Adams method. Numerical Algorithms, 36(1), 31-52.[Google Scholor]