Values of zeta-one functions at positive even integers

1. Introduction

et us start with the celebrated Euler-Goldbach Theorem. Say that a natural number \(p\) is a perfect power if \(p=n^{m}\) for some natural numbers \(m, n\ge2\).

Theorem 1.[Euler-Goldbach] \[ \sum_{p:\text{perfect power}}\frac{1}{p-1}=1. \]

See Bibiloni-Paradis-Viader [1] for history of this theorem. Recently, Shallit-Zikan [2] (1983) reinterpreted it in terms of Riemann's zeta function: the infinite series \begin{align*} \zeta(s)&=\sum_{n=1}^{\infty}\frac{1}{n^{s}}= \frac{1}{1^{s}}+\frac{1}{2^{s}}+\frac{1}{3^{s}}+\frac{1}{4^{s}}+\frac{1}{5^{s}}+\cdot\cdot\cdot \end{align*} is convergent for all complex numbers \(s\) such that Re\({(s)}>1\). Indeed, Euler proved that \[ \zeta(2k)=-\frac{1}{2}\frac{(2\pi i)^{2k}}{(2k)!}B_{2k}\,, \] where \(\{B_{n}\}\) are signed Bernoulli numbers; refer to Ayoub [3] for history of this function. Since \(\zeta(s)=1+\frac{1}{2^{s}}+\cdot\cdot\cdot>1\) and \[ 2> \frac{\pi^{2}}{6}=\zeta(2)>\zeta(3)>\zeta(4)>\zeta(5)>\cdot\cdot\cdot, \] we have \(1< \zeta(s)< 2\) for all \(s \ge 2 \). That is, \(\zeta(s)-1\) is the fractional part of \(\zeta(s)\). For example, \begin{align*} \zeta (2)-1&=0.6449\dots,\\ \zeta (3)-1&=0.2020\dots,\\ \zeta (4)-1&=0.0823\dots,\\ \zeta (5)-1&=0.0369\dots. \end{align*}

Theorem 2.Shallit-Zikan [2] \begin{align*} \sum_{k=2}^{\infty}(\zeta(k)-1)&=1. \end{align*}

Let us now see a similar result.

Theorem 3. See J.M. Borwein-Bradley-Crandall [4] \[ \sum_{k=1}^{\infty}(\zeta(2k)-1)=\frac{3}{4}. \]

Here we give a proof since it suggests some ideas for our main results.

Proof. Consider the double sequence \(a_{nk}=\left(\frac{1}{n^{2k}}\right)_{n\ge2, k\ge1}\) and positive series \(\sum\limits_{n\ge2, k\ge1}a_{nk}\). We find that \begin{align*} \sum_{n=2}^{\infty} \sum_{k=1}^{\infty}\frac{1}{n^{2k}} &= \sum_{n=2}^{\infty} \frac{1}{n^{2}} \sum_{k=0}^{\infty}\left(\frac{1}{n^{2}}\right)^{k} \\&=\sum_{n=2}^{\infty} \frac{1}{n^{2}} \frac{1}{1-\frac{1}{n^{2}}} = \sum_{n=2}^{\infty} \frac{1}{n^{2}-1} \\&= \frac{1}{2} \sum_{n=2}^{\infty} \left(\frac{1}{n-1}-\frac{1}{n+1}\right)= \frac{3}{4}\,, \end{align*} so that we can freely switch order of this series. As a consequence, $$\sum_{k=1}^{\infty}\left(\zeta(2k)-1\right)=\sum_{k=1}^{\infty}\sum_{n=2}^{\infty}\frac{1}{n^{2k}}=\sum_{n=2}^{\infty} \sum_{k=1}^{\infty}\frac{1}{n^{2k}}=\frac{3}{4}. $$

In this proof, the infinite series \(\sum\limits_{n=2}^{\infty} \frac{1}{n^{2}-1}\) appeared. It is now natural to think of analogous sums \(\sum\frac{1}{n^{s}\pm1}\). With this simple idea, this article introduces zeta-one functions \(\zeta_{+1}(s)\), \(\zeta_{-1}(s)\) and we compute values of \(\zeta_{+1}(2m)\) and \(\zeta_{-1}(2m)\) as main Theorems 4 and 5.

Theorem 4. \begin{align*} \zeta_{+1}(2m)&= -\frac{1}{2}+\frac{1}{2m}\sum_{k=1}^{m} \pi\alpha^{2k-1}\cot(\pi \alpha^{2k-1}). \end{align*}

Theorem 5. \[ \zeta_{-1}(2m)= \frac{\,1\,}{2}+\frac{2m-1}{4m}- \frac{\pi}{4m} \sum_{1\le k\le 2m-1, k\ne m} \beta^{k}\cot(\pi \beta^{k}). \]

2. Zeta-one functions

Throughout \(k, m, n, N\) and \(s\) each denote a nonnegative integer unless otherwise specified. Further, we assume that \(s\ge2\).

Definition 1. Define the zeta-one functions by \[ \zeta_{+1}(s)=\sum_{n=1}^{\infty}\frac{1}{n^{s}+1} \;\;\text{and}\;\; \zeta_{-1}(s)= \sum_{n=2}^{\infty} \frac{1}{n^{s}-1}\,. \] (For \(s\ge2\), these sums are indeed convergent as mentioned below). Call each zeta-plus-one and zeta-minus-one function, respectively.

Example 1. As seen above, \(\zeta_{-1}(2)=\frac{3}{4}\). Moreover, since \[ \coth(\pi z)=\frac{1}{\pi z}+\frac{1}{\pi} \sum_{n=1}^{\infty}\frac{2z}{z^{2}+n^{2}}, \;\; z\in\mathcal{C}, \] the substitution \(z=1\) implies that \[ \zeta_{+1}(2)= \sum_{n=1}^{\infty}\frac{1}{n^{2}+1}= -\frac{1}{2}+\frac{\pi}{2}\coth(\pi). \] As a consequence, \[ \zeta_{+1}(s)\le \zeta_{+1}(2)<\infty, \;\; \zeta_{-1}(s)\le \zeta_{-1}(2)<\infty \] for all \(s\ge2\).

3. Proof of Theorem

Toward the proof of Theorem 4 on \(\zeta_{+1}(2m)\), we need lemmas. For \(m\ge1\), set \[ f(z)=\frac{\cot(\pi z)}{z^{2m}+1} \;\; \text{and}\;\;\alpha=\exp\left(\frac{\pi i}{2m}\right). \] Recall that \[ \cot(\pi z)=\frac{1}{\pi z}+ \frac{1}{\pi}\sum_{n=1}^\infty \frac{2z}{z^2-n^2}, \;\; z\in \mathcal{C}. \] Thus, \(f\) is a meromorphic function with simple poles \(z=0,\pm1,\pm2,\pm3,\dotsb\) and \begin{align*} \alpha,\alpha^3,\alpha^5, \dotsb, \alpha^{2m-1},-\alpha,-\alpha^3,-\alpha^5, \dotsb, -\alpha^{2m-1} \end{align*} as all the roots of \(z^{2m}+1=0\). Let us compute the residue of \(f\) at each pole.

Lemma 1. For \(n=0, \pm1, \pm2, \pm3, \dotsb\), we have \[ \text{Res}(f, n)=\frac{1}{\pi(n^{2m}+1)}, \] and for \(1\le k\le m\), \[ \text{Res}(f,\pm\alpha^{2k-1})= - \frac{\alpha^{2k-1}{\cot(\pi \alpha^{2k-1})}}{2m}. \]

Proof. First, we have \begin{align*} \text{Res}(f,n)=&\lim_{z\to n}(z-n)f(z){}= \lim_{z\to n}\frac{z-n}{\sin\pi (z-n)}\cdot\frac{\cos(\pi z)}{z^{2m}+1}{} =\frac{1}{\pi (n^{2m}+1)}. \end{align*} Second, for \(1\le k\le m\), \begin{align*} \text{Res}(f,\alpha^{2k-1})&= \lim_{z\to \alpha^{2k-1}}(z-\alpha^{2k-1})f(z) \\&= \lim_{z\to \alpha^{2k-1}}(z-\alpha^{2k-1})\frac{\cot(\pi z)}{ z^{2m}+1} \\&= \lim_{z\to \alpha^{2k-1}}\cot(\pi z) \lim_{z\to \alpha^{2k-1}}\frac{z-\alpha^{2k-1}}{ z^{2m}+1} \\&= {\cot(\pi \alpha^{2k-1})} \lim_{z\to \alpha^{2k-1}}\frac{1}{ 2mz^{2m-1}} \;\; \text{(L'H\^{o}pital's rule)} \\&= {\cot(\pi \alpha^{2k-1})} \frac{1}{ 2m(\alpha^{2k-1})^{2m-1}} \\&=- \frac{\alpha^{2k-1}{\cot(\pi \alpha^{2k-1})}}{2m} \;\;{\left((\alpha^{2k-1})^{2m}=-1\right)}. \end{align*} It is quite similar to show that \[ \text{Res}(f, -\alpha^{2k-1})=-\frac{\alpha^{2k-1}\cot(\pi\alpha^{2k-1})}{2m}. \]

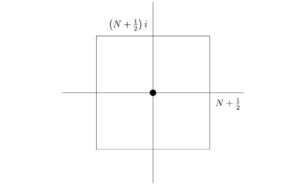
Lemma 2. For a positive integer \(N\), consider line segments on the complex plane \begin{align*} C_{1}(N)&= \left\{\left(N+\frac{1}{2}\right)+yi \right\}{-\left(N+\frac{1}{2}\right)\le y\le {N+\frac{1}{2}}}, \\C_{2}(N)&= \left\{x+\left(N+\frac{1}{2}\right)i \right\}{-\left(N+\frac{1}{2}\right)\le x\le {N+\frac{1}{2}}}, \\C_{3}(N)&= \left\{-\left(N+\frac{1}{2}\right)+yi \right\}{-\left(N+\frac{1}{2}\right)\le y\le {N+\frac{1}{2}}}, \\C_{4}(N)&= \left\{x-\left(N+\frac{1}{2}\right)i \right\}{-\left(N+\frac{1}{2}\right)\le x\le {N+\frac{1}{2}}}\,, \end{align*} and set \(C(N)=C_{1}(N)\cup C_{2}(N)\cup C_{3}(N)\cup C_{4}(N).\)

1. If \(z\in C(N)\), then \(|\cot(\pi z)|\le \coth{\frac{3}{2}\pi}\).
2. If \(z\in C(N)\), then \[\left| \frac{1}{z^{2m}+1}\right|\le \frac{1}{ \left(N+\frac{1}{2}\right)^{2m}-1}. \]

Proof.

1. Suppose \(z\in C(N)\). If \(z\in C_{1}(N)\), then write \[ z=\left(N+\frac{1}{2}\right)+yi, \;\; -\left(N+\frac{1}{2}\right)\le y\le {N+\frac{1}{2}}.\] \begin{align*} |\cot\pi z|&= { \frac{e^{\pi i z}+e^{-\pi i z} }{ e^{\pi i z}-e^{-\pi i z}} } = | \frac{ e^{-\pi y}e^{\left(N+\frac{1}{2}\right)\pi i} +e^{\pi i y}e^{-\left(N+\frac{1}{2}\right)\pi i }}{ e^{-\pi y}e^{\left(N+\frac{1}{2}\right)\pi i} -e^{\pi i y}e^{-\left(N+\frac{1}{2}\right)\pi i } } | \\&= | \frac{ e^{-\pi y}(-1)^{N}i +e^{\pi i y}(-1)^{N}(-i) } { e^{-\pi y}(-1)^{N}i -e^{\pi i y}(-1)^{N}(-i) } | \\&= | \frac{e^{-\pi y}-e^{\pi i y} } { e^{-\pi y}+e^{\pi i y}} | = | \frac{e^{\pi i y}-e^{-\pi y} } { e^{\pi i y}+e^{-\pi y} } | \\&=|\tanh(y)|\le 1< \coth\frac{3}{2}\pi\,\, (=1.00016\cdot\cdot\cdot). \end{align*} If \(z\in C_{2}(N)\), then \[ z=x+ \left(N+\frac{1}{2}\right)i, \;\; -\left(N+\frac{1}{2}\right)\le x\le {N+\frac{1}{2}} \,,\] and \begin{align*} |\cot(\pi z)|&= \left| \frac{e^{\pi i z}+e^{-\pi i z}} {e^{\pi i z}-e^{-\pi i z}} \right| \\&\le \frac{|e^{\pi i z}|+|e^{-\pi i z}|}{|e^{\pi i z}|-|e^{-\pi i z}|} \\&= \frac{|e^{-\pi (N+1/2)}|+|e^{\pi (N+1/2)}|}{|e^{-\pi (N+1/2)}|-|e^{\pi (N+1/2)}|} \\&=\frac{e^{\pi i \left(N+\frac{1}{2}\right)}+e^{-\pi \left(N+\frac{1}{2}\right)} }{e^{\pi i \left(N+\frac{1}{2}\right)}-e^{-\pi \left(N+\frac{1}{2}\right)}} \\&=\coth\left(N+\frac{1}{2}\right)\pi\le \coth\frac{3}{2}\pi\,, \end{align*} since \(t\mapsto \coth(t)\) is decreasing for \(t>0\). For \(z\in C_{3}(N)\cup C_{4}(N)\), we have \(-z\in C_{1}(N)\cup C_{2}(N)\) so that \[ |\cot(\pi z)|= |-\cot(\pi (-z))|= |\cot(\pi (-z))|\le \coth\frac{3}{2}\pi. \]
2. If \(z\in C(N)\), then \(|z|\ge N+\frac{1}{2}\). Consequently, \(|z|^{2m}-1\ge \left(N+\frac{1}{2}\right)^{2m}-1 \), \[ \frac{1}{|z|^{2m}-1}\le \frac{1}{\left(N+\frac{1}{2}\right)^{2m}-1}, \] \( \frac{1}{|z^{2m}+1|}\le \frac{1}{|z|^{2m}-1}\le \frac{1}{\left(N+\frac{1}{2}\right)^{2m}-1}. \)

Proof.[Proof of Theorem 4] Let \(s\) be a positive even integer, say \(s=2m\), \(m\ge1\). Further, let \(\alpha=\alpha_{2m}=\exp\left(\frac{\pi i}{2m}\right)\) for convenience. View \(C(N)=C_{1}(N)+C_{2}(N)+C_{3}(N)+C_{4}(N)\) above as the sum of four paths with counterclockwise orientation. Notice that any pole of \(f\) does not lie on \(C(N)\). We are going to compute the integral \[ I_{N}=\int_{C(N)}f(z)dz. \] Let \(D(N)\) be the domain enclosed by \(C(N)\). Then, the residue theorem with Lemma 1 claims that \begin{align*} I_{N}&=\int_{C{(N)}}f(z)dz \\&= 2\pi i \sum_{a: \text{pole of} f(z)| a\in D(N)} \text{Res}(f, a) \\&= 2\pi i \left(\text{Res}(f, 0)+ \sum_{n=1}^{N} \left(\text{Res}(f, n)+\text{Res}(f, -n)\right) + \sum_{k=1}^{m} \left(\text{Res}(f, \alpha^{2k-1})+\text{Res}(f, -\alpha^{2k-1})\right)\right) \\&= 2\pi i \left(\frac{1}{\pi}+2 \sum_{n=1}^{N}\frac{1}{\pi(n^{2m}+1)}+2\left(-\sum_{k=1}^{m}\frac{\alpha^{2k-1}\cot(\pi\alpha^{2k-1})}{2m} \right)\right)\,, \end{align*} while Lemma 2 implies \begin{align*} |I_{N}|&=\left|\int_{C{(N)}}f(z)dz\right| \le \int_{C{(N)}}|f(z)|dz \le \frac{\coth\frac{3}{2}\pi}{ \left(N+\frac{1}{2}\right)^{2m}-1 } \int_{C{(N)}}dz \\&=\frac{\coth\frac{3}{2}\pi}{ \left(N+\frac{1}{2}\right)^{2m}-1 }\cdot 8\left(N+\frac{1}{2}\right)\to 0 \;\; (N\to \infty). \end{align*} Therefore, taking the limit \(N\to\infty\) for \(I_{N}\) yields \[ 0= 2\pi i \left(\frac{1}{\pi}+\frac{2}{\pi}\zeta_{+1}(2m)-2 \sum_{k=1}^{m}\frac{\alpha^{2k-1}\cot(\pi\alpha^{2k-1})}{2m}\right) . \] Conclude that \[ \zeta_{+1}(2m)= -\frac{1}{2}+\frac{1}{2m}\sum_{k=1}^{m} \pi\alpha^{2k-1}\cot(\pi \alpha^{2k-1}). \]

Of course, \(\zeta_{+1}(2m)\) is a real number so that there should be some expression of \(\zeta_{+1}(2m)\) in terms of only real trigonometric functions.

Example 2. Let \(s=4, m=2\) and \(\alpha=\alpha_{4}=\exp\left(\frac{\pi i}{4}\right)\). Then \begin{align*} \zeta_{+1}(4)=\sum_{n=1}^\infty \frac{1}{n^{4}+1}&=-\frac{1}{2}+\frac{\pi}{4}\sum_{k=1}^2 \alpha^{}\cot(\pi \alpha^{}){}\\ &=-\frac{1}{2}+\frac{\pi}{4} \left(\alpha \cot(\pi \alpha^{})+\alpha^{3} \cot(\pi \alpha^{3})\right) {}\\ &=-\frac{1}{2}+\frac{\pi}{4} \left(\alpha \cot(\pi \alpha)+\alpha^{-1} \cot(\pi \alpha^{-1})\right) .\end{align*} Now, it follows from the facts \[\pi \exp\left(\frac{\pi i}{4}\right) =\frac{1\pm i}{\sqrt2} \pi \;\; \text{and} \;\; \cot(x+yi)=\frac{\sin2x-i\sinh2y}{\cosh2y-\cos2x} \;\; x, y\in \mathcal{R} \,,\] that \begin{align*} \zeta_{+1}(4)&= -\frac{1}{2}+\frac{\pi}{4} \left(\alpha \cot(\pi \alpha)+\alpha^{-1} \cot(\pi \alpha^{-1})\right) \\&= -\frac{1}{2}+ \frac{\pi}{4} \left( \frac{1+i}{\sqrt{2}}\cdot\frac{\sin\sqrt{2}\pi-i\sinh\sqrt{2}\pi}{\cosh\sqrt{2}\pi-\cos\sqrt{2}\pi} + \frac{1-i}{\sqrt{2}}\cdot\frac{\sin\sqrt{2}\pi+i\sinh\sqrt{2}\pi}{\cosh\sqrt{2}\pi-\cos\sqrt{2}\pi} \right) \\&= -\frac{1}{2}+\frac{\sqrt2 \pi}{4} \left(\frac{ \sin\sqrt2 \pi+ \sinh\sqrt2 \pi}{\cosh\sqrt2 \pi-\cos\sqrt2 \pi}\right). \end{align*} Let \(s=6\), \(m=3\) and \(\alpha=\alpha_{6}=\exp\left(\frac{\pi i}{6}\right)=\frac{\sqrt{3}+i}{2}\). With \(\alpha^{3}=i\), \(\alpha^{5}=\alpha^{-1}=\frac{\sqrt{3}-i}{2}\) and \(i\cot(\pi i)=\coth(\pi) \), we observe that \begin{align*} \zeta_{+1}(6)&= -\frac{1}{2}+\frac{\pi}{6} \left(\alpha\cot(\pi \alpha)+ {\alpha^{3}\cot(\pi \alpha^{3})} +\alpha^{5}\cot(\pi \alpha^{5})\right) \\ &= -\frac{1}{2}+\frac{\pi}{6} \left(\alpha\cot(\pi \alpha)+ \alpha^{-1}\cot(\pi \alpha^{-1}) + i\cot(\pi i) \right) \\ &= -\frac{1}{2}+\frac{\pi}{6} \left( \frac{\sqrt{3}+i}{2}\cdot \frac{\sin\sqrt{3}\pi-i\sinh\pi}{\cosh\pi-\cos\sqrt{3}\pi} + \frac{\sqrt{3}-i}{2}\cdot \frac{\sin\sqrt{3}\pi+i\sinh\pi}{\cosh\pi-\cos\sqrt{3}\pi} +\coth(\pi) \right) \\&= -\frac{1}{2}+\frac{\pi}{6}\left( \frac{\sqrt3 \sin\sqrt3 \pi+\sinh\pi}{\cosh\pi-\cos\sqrt3 \pi }+\coth(\pi)\right). \end{align*}

4. Proof of Theorem 5

Next, we prove Theorem 5 on \(\zeta_{-1}(2m)\). Ideas are quite same. For \(m\ge1\), let \[ g(z)=\frac{\cot(\pi z)}{z^{2m}-1} \;\; \text{and}\;\; \beta=\exp\left(\frac{\pi i}{m}\right). \] It has poles at \(z=0, \pm1, \pm 2, \pm3, \dots,\) and \(z=\beta^{k}\), \(1\le k\le 2m-1, k\ne m\). The order of the poles \(z=\pm1\) is 2 and the all others are simple.

Lemma 3. For \(n=0, \pm2, \pm3, \dots\), we have \[ \text{Res}(g, n)=\frac{1}{\pi(n^{2m}-1)}, \] for \(1\le k\le 2m-1, k\ne m\), \[\text{Res}(\pi, \beta^{k})=\frac{\beta^{k}}{2m}\cot(\pi \beta^{k}) \,,\] and moreover \[ \text{Res}(g, \pm1)=-\frac{2m-1}{4m\pi}. \]

Proof. The proofs of the first two equalities are almost similar to ones for Lemma 1. Thus we only need to show \(\text{Res}(g, \pm1)=-\frac{2m-1}{4m\pi}\). Let \(\phi(z)= \sum\limits_{k=0}^{2m-1}z^{k}\). Notice that \(\phi(z)=(z^{2m+1}-1)/(z-1)\). Then \begin{align*} \text{Res}(g, 1)&=\lim_{z\to 1}{ \frac{d}{dz}(z-1)^{2}g(z)} \\&=\lim_{z\to 1}{ \frac{d}{dz}(z-1)\cot(\pi z)\cdot\frac{1}{\phi(z)}} \\&= \lim_{z\to 1}\left( \frac{\cot(\pi z)-\pi(z-1)(\cot^{2}\pi z+1)}{\phi(z)} - (z-1)\cot(\pi z)\frac{\phi'(z)}{\phi(z)^{2}} \right). \end{align*} Let us see the first term. Immediately, \(\lim_{z\to 1}\phi(1)=2m\) and \begin{align*} \lim_{z\to 1} \left( \cot(\pi z)-\pi(z-1)(\cot^{2}\pi z+1)\right) & = \lim_{w\to 0}\left( \cot(\pi w)-\pi w(\cot^{2}\pi w+1)\right) \\&= \lim_{w\to 0} \left( \cot(\pi w)(1-\pi w\cot(\pi w))\right) -\lim_{w\to 0}{\pi w} \\&= \lim_{w\to 0} { \frac{\tan(\pi w)-\pi w}{\tan^{2}\pi w}} -0 \\&= \lim_{w\to 0}{ \frac{\pi (1+\tan^{2}\pi w)-\pi} {2\pi \tan \pi w(1+\tan^{2}\pi w)} } =0. \;\; \text{(L'H\^{o}pital's rule)} \end{align*} In addition, since \[ \phi'(1)= \sum_{k=0}^{2m-1}k =m(2m-1), \] the limit \(z\to1\) for the second term is \begin{align*} \lim_{z\to 1}{ \left(-(z-1)\cot(\pi z)\frac{\phi'(z)}{\phi(z)^{2}}\right) } &=- \lim_{w\to 0} {w\cot(\pi w) \frac{\phi'(w-1)}{\phi(w-1)^{2}} } \\&=-\frac{1}{\pi}\frac{m(2m-1)}{(2m)^{2}} =-\frac{2m-1}{4m\pi}. \end{align*}

Proof.[Proof of Theorem 5] Let \(\beta=\exp(\frac{\pi i}{m})\) be as above. Further, let \(N, C(N), D(N)\) be as in the previous section. Again, the residue theorem claims that \[ \int_{C(N)}{g(z)}\,dz= 2\pi i \sum_{ \substack{\text{\(a\):pole of \(g\)}\\ a\in D(N)} }\text{Res}(g, a). \] Taking the limit \(N\to \infty\), the integral converges to 0 likewise. It follows from Lemma 3 that \begin{align*} 0&=2\pi i \sum_{a:\text{pole of \(g\)}}\text{Res}(g, a), \end{align*} \begin{align*}0&= \text{Res}(g, 0)+\text{Res}(g, 1)+\text{Res}(g, -1)+ \sum_{n=2}^{\infty} \left(\text{Res}(g, n)+ \text{Res}(g, -n)\right) + \sum_{1\le k\le 2m-1, k\ne m} \frac{\pi }{2m} \beta^{k}\cot(\pi \beta^{k}) \\&= -\frac{1}{\pi }-\frac{2m-1}{2m}\pi +\frac{2}{\pi }\zeta_{-1}(2m)+ \sum_{1\le k\le 2m-1, k\ne m} \frac{\pi }{2m} \beta^{k}\cot(\pi \beta^{k}). \end{align*} Conclude that \[ \zeta_{-1}(2m)= \frac{\,1\,}{2}+\frac{2m-1}{4m}- \frac{\pi}{4m} \sum_{1\le k\le 2m-1, k\ne m} \beta^{k}\cot(\pi \beta^{k}). \]

Example 3. For \(s=4, m=2, \beta=\exp\left(\frac{\pi i}{2}\right)=i\), an expression of real trigonometric function for \(\zeta_{-1}(4)\) is \[ \zeta_{-1}(4)= \frac{1}{2}+\frac{3}{8}-\frac{\pi}{8} \left(i\cot(\pi i)+i^{3}\cot(\pi i^{3})\right) = \frac{7}{8}-\frac{\pi}{4}\coth(\pi). \] Notice that this also shows that \[ \sum_{k=1}^{\infty}\left(\zeta(4k)-1\right) =\frac{7}{8}-\frac{\pi}{4}\coth(\pi) \] as in [4, 263]. For \(s=6, m=3, \beta=\exp\left(\frac{\pi i}{3}\right)\), we see that \begin{align*} \zeta_{-1}(6)& =\frac{1}{2}+\frac{5}{12} -\frac{\pi}{12} \left( e^{\pi i/3}\cot(\pi e^{\pi i/3}) + e^{-\pi i/3}\cot(\pi e^{-\pi i/3} ) + e^{2\pi i/3}\cot(\pi e^{2\pi i/3}) + e^{-2\pi i/3}\cot(\pi e^{-2\pi i/3} )\right)\\ &= \frac{11}{12}-\frac{\pi}{12} \left( \frac{\sqrt{3}\sinh \sqrt{3}\pi}{\cosh\sqrt{3}\pi+1} + \frac{\sqrt{3}\sinh \sqrt{3}\pi}{\cosh\sqrt{3}\pi+1} \right)\\ &= \frac{11}{12}-\frac{\pi}{12} \left( \,2\sqrt{3}\, \frac{2\sinh \frac{\sqrt{3}}{2}\pi\cosh \frac{\sqrt{3}}{2}\pi} {2\cosh^{2} \frac{\sqrt{3}}{2}\pi} \right)\\ &=\frac{11}{12}-\frac{\sqrt{3}}{6}\pi\tanh{\frac{\sqrt{3}}{2}\pi}. % =0.017593\cd. \end{align*}

Acknowledgments

The first author thanks Satomi Abe, Shoko Asami and Michihito Tobe for sincerely supporting him. Also, the authors would like to thank Shigeru Iitaka. This research project arose from his online seminar in 2020-2022.

Conflicts of Interest

The authors declare no conflict of interest.