Open Journal of Mathematical Sciences
Vol. 7 (2023), Issue 1, pp. 160 – 171
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2023.0204

Effects of thermal dispersion on transient free convective flow in vertical porous channel filled with porous material

Babatunde Aina\(^{1}\) and Basant K. Jha\(^{2,*}\)
\(^{1}\) Department of Mathematics, Federal University, Gashua, Nigeria.
\(^{2}\) Department of Mathematics, Ahmadu Bello University, Zaria, Nigeria.
Correspondence should be addressed to Basant K. Jha at basant777@yahoo.co.uk

Copyright © 2023 Babatunde Aina and Basant K. Jha. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: January 1, 2022 – Accepted: March 18, 2023 – Published: April 1, 2023

Abstract

In this work, the effect of suction/injection on transient free convective flow in vertical porous (suction/injection on the channel surfaces) channel filled with porous material in the presence of thermal dispersion was studied. The Boussinesq assumption is applied and the nonlinear governing equations of motion and energy are developed. The time dependent problem is solved using implicit finite difference method while steady state problem is solved by perturbation technique method. The solution obtained is graphically represented and the effects of suction/injection, time, Darcy number, thermal dispersion, and Prandtl number on the fluid flow and heat transfer characteristics. During the course of computation, an excellent agreement was found between the well-known steady state solutions sand transient solutions at large value of time. Furthermore, the time required to reach steady state velocity and temperature field strongly dependent on suction/injection parameter, Prandtl number and thermal dispersion parameter. The introduction of suction/injection has distorted the symmetric nature of the flow formation.

Keywords:

Suction/Injection; Transient Free Convective; Thermal Dispersion; Darcy number; Vertical Porous Channel.

1. Introduction

Because of its relevance to a variety of applications including solar receiver devices, building thermal insulation, heat exchangers, energy storage units, ceramic processing, catalytic reactors and energy recovery in high temperature furnaces, convection in porous media is a well-developed field of investigation. Many studies have been conducted on unsteady and steady free convective flow in vertical channel filled with porous material under different physical situations (see refs. [1,2, 3]). A numerical study of natural convection inside a porous wavy cavity filled with a nanofluid under the effect of thermal dispersion has been carried out using the Forchheimer-Buongiomo approach by Sheremet et al., [4]. Umavathi et al., [5] investigate the combined effect of variable viscosity and thermal conductivity on mixed convection flow of a viscous fluid in a vertical channel in the presence of first order chemical reaction. Kasaeipour et al., [6] studied on free convection heat transfer and entropy generation analysis of MWCNT-Mgo water nanofluid using Lattice Boltzmann method in cavity with refrigerant solid body experimental thermo-physical properties. Rahimi et al., [7] investigate the free convection heat transfer performance using Lattice Boltzmann method within the cavities filled with nanofluid in existence of internal rigid bodies.

The natural convection heat transfer analysis is performed by different approaches such as headline visualization, total and local entropy generation, average and local nusselt number using Lattice Boltzmann method in nanofluid filled cavity with partially heated and cooled walls included by internal heaters was carried out by Rahimi et al., [8]. Salari et al., [9] reported a numerical study of the natural convection and entropy generation for a layered fluid system in a cuboid enclosure which is differentially heated from sides and filled by two immiscrible gas/liquid fluids. Three dimensional natural convection in a rectangle cuboid filled by two immiscible fluid of water and air at different liquid height ratio has been studied experimentally and numerically by Malekshak and Salari [10]. Al-Rashed et al., [11] evaluate numerically entropy generation inside an inclined cubical differentially heated cavity wit CNT- water nanofliud using FVM based on 3D vertically-vector potential formalism.

On the other hand, the thermal dispersion occurs term exists as a result of both the micro-structure of the porous material as well as the heat convection effect. One of the most important applications of including thermal dispersion effect in the mathematical modelling of the heat equation is the manufacturing processes of polymer composites such as liquid composite molding. However, all the above literature review indicates that there is still a scarcity of research on unsteady free convective flow in vertical channel filled with porous material. Murthy and Singh [12] have reported in a paper about the effect of viscous dissipation on a non-Darcy natural convection boundary layer along an isothermal vertical wall embedded in a fluid saturated porous medium, that in the case when inertia terms are prevalent, the thermal dispersion effects will become important. However, Hong and Tien [1]30} have analyzed the problem of thermal dispersion effects on natural convection about a heated horizontal cylinder in an enclosed porous medium. Hsiao et al., [13] discussed the influences of non-uniform porosity and thermal dispersion on natural convection about a heated horizontal cylinder in an enclosed porous medium. Moreover, Hsiao et al., [14] concluded that the effects of variable porosity and thermal dispersion increases the average Nusselt number and reduces the error between the experimentl data available and their solutions. Kuznetsov [15] presented an analytical study of the effect of the transverse thermal dispersion on fully developed forced convection in a parallel plate channel filled with an isotropic fluid saturated porous medium.

Meanwhile, Amiri and Vafai [16] suggested accounting for thermal dispersion by assuming that the effective thermal conductivity consists of both stagnant and dispersion conductivity. In their study, they constructed their correlation based on the experimental findings of Wakao and Kaguei [17]. Sheremet and Bachok [18] examined the effect of thermal dispersion on transient natural convection in a wavy-walled porous cavity filled with a nanofluid. Adil et al., [19] study focused on the well-established improved perturbed {NLSE}~with the Kerr law non-linearity equation model. The model is integrated with the help of the extended V-expansion method. Faridi et al., [20] examined the fractional analysis of fusion and fission process in plasma physics. Asjad et al., [21] carried out the study on the fractional comparative study of the non-linear directional couplers in non-linear optics.}

Recently, Jha and Aina [22] carried out numerical analysis on transient free convective flow in vertical channel filled with porous material in presence of thermal dispersion. They reported in their study that velocity and temperature is enhanced with the increase in thermal dispersion parameter as well as time. From all the above discussed work, these effects were studied and they have confirmed the importance of thermal dispersion effects studied in these papers. {Therefore, as a follow-up study of Jha and Aina [22], here, we include the effects of suction/injection in the fluid. Suction or injection of fluid through the bounding surfaces, as, for example, in mass transfer cooling, it can significantly change the flow field and, as a consequence, affect the rate of heat transfer from the bounding surfaces. In general, suction tends to increase the skin-friction and heat transfer coefficients whereas injection acts in the opposite manners. Injection or suction of fluid through porous heated or cooled surface is of general interest in practical problems involving film cooling, control of boundary layers, etc. This can lead to enhanced heating (or cooling) of the system and can help to delay the transition from laminar flow. The current work is aimed as an extension of the previous analytical studies to provide some insight into a number of industrial applications, which use similar configurations.

2. Mathematical Analysis

Consider the unsteady free convective flow in vertical porous channel formed by two infinite vertical parallel porous plates filled with porous material in the pressure of thermal dispersion. Figure 1 represents the configuration of studied geometry in this work where \(x' -\)axis is taken along one of the channel plates and the \(y' -\)axis is taken normal to the channel porous plates. Both the channel porous plates are assumed to be separated by a width \(2h\). The flow is assumed transient and fully developed. At time \(t' \leq 0,\) the fluid, and porous plates are assumed to be same temperature \(T_{0}\), and there is no fluid motion. At time greater than zero, i.e. \(t' > 0,\) the temperature of the channel plates at \(y' = - h\) is raised to \(T_{w},\) due to temperature gradient between the plates, natural convection flow occurs in the channel. Furthermore, at the same time the flow is subjected to suction of the fluid from left vertical porous plate and at the same rate fluid is being injected through the right vertical porous plate. Recently, Jha and Aina [22] carried out numerical analysis on transient free convective flow in vertical channel filled with porous material in presence of thermal dispersion.

Figure 1. Physical model and coordinate system.

Following Jha and Aina [22] and considering the effect of suction/injection in the fluid, the mathematical model for the present physical situation under Boussinesq's approximation in dimensional form is:

\begin{equation}\tag{1}\label{e1}\frac{\partial u'}{\partial t'} = \nu_{\text{eff}}\frac{\partial^{2}u'}{\partial y'^{2}} + g\beta\left( T - T_{0} \right) - \frac{\nu}{K}u', \end{equation}

\begin{equation}\tag{2}\label{e2}\frac{\partial T'}{\partial t'} + V_{0}\frac{\partial T'}{\partial y'} = \frac{k_{f}}{\rho C_{\rho}}\frac{\partial}{\partial y'}\left\lbrack \left( \frac{k_{m}}{k_{f}} + C\Pr\frac{u'}{\nu}\text{dp} \right)\frac{\partial T'}{\partial y'} \right\rbrack. \end{equation}

The initial and boundary condition to be satisfied are:

\begin{equation}\tag{3}\label{e3} h\begin{cases} t' \leq 0: \quad u' = 0,\quad T' = T_{0}\quad \text{for}\quad - h \leq y' \leq h,\\ t^{'} > 0 :\quad \left\{ \begin{matrix} u^{'} = 0;\ T^{'} = T_{w},\ \ \ \ \ \text{at}\quad y^{'} = - h\ \\ u^{'} = 0;\ T^{'} = T_{0},\ \ \ \ \ \text{at}\quad y^{'} = + h \end{matrix} \right.\end{cases} \end{equation}

Eqs. (\ref{e1}) - (\ref{e3}) can be nondimensionalized using the following variables

\begin{equation}\tag{4}\label{e4} \begin{cases}t = \frac{t'\nu}{h^{2}},\quad y = \frac{y'}{h},\quad U = \frac{u'}{u_{0}}, \quad \theta = \frac{T' - T_{0}}{T_{w} - T_{0}}, \quad u_{0} = g\beta{\left( T_{w} - T_{0} \right)h^{2}}{\nu},\\ \Pr = \frac{C_{p}\mu}{k},\quad \gamma = \frac{\nu_{\text{eff}}}{\nu},\quad Da = \frac{k}{h^{2}},\quad kr = \frac{k_{m}}{k_{f}},\quad S = \frac{V_{0}h}{\nu},\quad Gr = \frac{u_{0}\text{dp}}{\nu}.\end{cases} \end{equation}

The physical quantities used in the above equations are defined in the nomenclature. Substituting Eq. (\ref{e4}) into Eqs. (\ref{e1}) - (\ref{e3}), the dimensionless momentum and energy equations are:

\begin{align}\tag{5}\label{e5}&\frac{\partial U}{\partial t} + S\frac{\partial U}{\partial y} = \gamma\frac{\partial^{2}U}{\partial y^{2}} + \theta - \frac{U}{\text{Da}}\\ &\frac{\partial\theta}{\partial t} + S\frac{\partial\theta}{\partial y} = \frac{1}{\Pr\frac{k_{m}}{k_{f}}\frac{\partial^{2}\theta}{\partial y^{2}}\frac{\partial}{\partial y}\left( U\frac{\partial\theta}{\partial y} \right)}.\tag{6}\label{e6}\end{align}

The corresponding initial and boundary conditions for these equations in dimensionless form are given by

\begin{equation}\tag{7}\label{e7} \begin{cases} t \leq 0:\quad U = 0,\quad \theta = 0\quad \text{for}\quad - 1 \leq y' \leq 1,\\ t^{'} > 0\ :\ \left\{ \begin{matrix} U = 0;\ \theta = 1,\ \ \ \ \ \text{at}\quad y^{'} = - 1, \\ U = 0;\ \theta = 0,\ \ \ \ \ \text{at}\quad y^{'} = + 1 \\ \end{matrix} \right.\end{cases} \end{equation}

3. Analytical solutions

The governing Eqs. (\ref{e5}) and (\ref{e6}) presented in the previous section are highly nonlinear and exhibit no analytical solutions. The importance of analytical solutions which refers to steady natural convection flow in vertical porous channel filled with porous material in the presence of thermal dispersion relies on the chance to obtain nontrivial benchmarks to test the reliability of numerical codes developed for more complex physical situations. Analytical solutions are often an opportunity to inspect the internal consistency of mathematical models and of the approximations adopted, as well as to develop new theoretical results. The mathematical model representing the steady state natural convection flow in vertical porous channel filled with porous material in the presence of thermal dispersion can be obtained by setting \(\frac{\partial U}{\partial t} = 0\) and \(\frac{\partial\theta}{\partial t} = 0\) in Eqs. (\ref{e5}) and (\ref{e6}) to get:

\begin{align}\tag{8}\label{e8} &\gamma\frac{d^{2}U}{dy^{2}} - S\frac{\text{dU}}{\text{dy}} - \frac{U}{\text{Da}} + \theta = 0,\\ &\frac{k_{m}}{k_{f}}\frac{d^{2}\theta}{dy^{2}} - S\Pr\frac{d\theta}{dy} + Gr\Pr C\frac{d}{\text{dy}}\left( U\frac{d\theta}{dy} \right) = 0.\tag{9}\label{e9}\end{align}

The boundary conditions are

\begin{equation}\tag{10}\label{e10} \begin{cases} U = 0,\quad \theta = 1,\quad \text{at} \quad y = - 1,\\ U = 0,\quad \theta = 0,\quad \text{at}\quad y = 1.\end{cases} \end{equation}

The above equations under given boundary conditions are solved by perturbation method. In order to construct an approximate solutions of Eqs. (\ref{e8}) and (\ref{e9}), subject to the boundary conditions in Eq. (\ref{e10}), we employed a regular perturbation method by taking a power series expansion in the thermal dispersion parameter \(C\) such as:

\begin{align}\tag{11}\label{e11} &U\left( y \right) = U_{0}\left( y \right) + \varepsilon U_{1}\left( y \right) + \varepsilon^{2}U_{2}\left( y \right) + ... = \sum_{i = 0}^{\infty}{\varepsilon^{i}U_{i}\left( y \right)},\\ &\tag{12}\label{e12}\theta\left( y \right) = \theta_{0}\left( y \right) + \varepsilon\theta_{1}\left( y \right) + \varepsilon^{2}\theta_{2}\left( y \right) + ... = \sum_{i = 0}^{\infty}{\varepsilon^{i}\theta_{i}\left( y \right)}. \end{align}

A two term expansion has been used here and terms smaller than \(O\left( \varepsilon^{2} \right)\), where \(\varepsilon = Gr*{\Pr*}C\) are neglected. Here \(\varepsilon\)is chosen as our perturbation parameter. Obviously, the results are only valid for \(\varepsilon < < 1\), as was the case in experiments reported in [23] and it will be shown that for most cases of practical interest, for which experiments are conducted, this requirement is met. One can now obtain the zeroth and first order equations as

\begin{align}\tag{13}\label{e13} &\gamma\frac{d^{2}U_{0}}{dy^{2}} - S\frac{dU_{0}}{\text{dy}} - \frac{U_{0}}{\text{Da}} + \theta_{0} = 0,\\ &\tag{14}\label{e14}\frac{k_{m}}{k_{f}}\frac{d^{2}\theta_{0}}{dy^{2}} - S\Pr\frac{d\theta_{0}}{\text{dy}} = 0,\\ &\tag{15}\label{e15}\gamma\frac{d^{2}U_{1}}{dy^{2}} - S\frac{dU_{1}}{\text{dy}} - \frac{U_{1}}{\text{Da}} + \theta_{1} = 0,\\ &\tag{16}\label{e16}\frac{k_{m}}{k_{f}}\frac{d^{2}\theta_{1}}{dy^{2}} - S\Pr\frac{d\theta_{1}}{\text{dy}} + Gr\Pr\frac{d}{\text{dy}}\left( U_{0}\frac{d\theta_{0}}{\text{dy}} \right) = 0.\end{align}

The boundary conditions to be satisfied are:

\begin{equation}\tag{17}\label{e17} \begin{cases} U_{0} = U_{1} = \theta_{1} = 0,\theta_{0} = 1,\quad \text{at}\quad y = - 1,\\ U_{0} = U_{1} = \theta_{0} = \theta_{1} = 0,\quad\text{ at}\quad y = 1.\end{cases}\end{equation}

The zeroth order solution can be obtained as

\begin{equation}\tag{18}\label{e18} \begin{cases} U_{0}\left( y \right) = \left\lbrack D_{3}{\cos h}\left(\delta y \right) + D_{4}{\sin h}\left( \delta y \right) \right\rbrack\exp\left( 0.5Sy \right) - \left\lbrack \frac{D_{1}\exp\left( A_{1}y \right)}{A_{3}} \right\rbrack + D_{2}\text{Da},\\ \theta_{0}\left( y \right) = D_{1}\exp\left( A_{1}y \right) + D_{2}.\end{cases}\end{equation}

The first order solution can be obtained as

\begin{align}\tag{19}\label{e19} \begin{cases}U_{1}\left( y \right) &= \left\lbrack D_{7}{\cos h}\left( \delta y \right) + D_{8}{\sin h}\left( \delta y \right) \right\rbrack\exp\left( 0.5Sy \right) - \frac{D_{5}\text{Da}}{A_{1}} - \frac{D_{6}\exp\left( A_{1}y \right)}{A_{3}} - \frac{A_{6}\exp\left( A_{10}y \right)}{A_{14}} - \frac{A_{7}\exp\left( A_{11}y \right)}{A_{15}}\\ &\;\;\;+ \frac{A_{8}\exp\left( 2A_{1}y \right)}{A_{16}} + A_{12}\exp\left( A_{1}y \right) + A_{13}y\exp\left( A_{1}y \right)\\ \theta_{1}\left( y \right) &= - \frac{D_{5}}{A_{1}} + D_{6}\exp\left( A_{1}y \right) + A_{6}\exp\left( A_{4}y \right) + A_{7}\exp\left( A_{5}y \right) - A_{8}\exp\left( 2A_{1}y \right) + A_{9}y\exp\left( A_{1}y \right).\end{cases}\end{align}

Using (\ref{e18}) and (\ref{e19}), we write the steady state skin frictions on the porous plates are

\begin{align}\tag{20}\label{e20} &\tau_{0} = \left. \ \frac{\text{dU}}{\text{dy}} \right|_{y = 0} = \left. \ \frac{dU_{0}}{\text{dy}} \right|_{y = 0} + \varepsilon\left. \ \frac{dU_{1}}{\text{dy}} \right|_{y = 0},\\ &\tag{21}\label{e21}\tau_{1} = \left. \ \frac{\text{dU}}{\text{dy}} \right|_{y = 1} = \left. \ \frac{dU_{0}}{\text{dy}} \right|_{y = 1} + \varepsilon\left. \ \frac{dU_{1}}{\text{dy}} \right|_{y = 1}.\end{align}

Finally, the Nusselt number \(\left( \text{Nu} \right)\) on the porous plates are:

\begin{align}\tag{22}\label{e22} &Nu_{0} = \left. \ \frac{dU}{dy} \right|_{y = 0} = \left. \ \frac{d\theta_{0}}{\text{dy}} \right|_{y = 0} + \varepsilon\left. \ \frac{d\theta_{1}}{\text{dy}} \right|_{y = 0},\\ &\tag{23}\label{e23}Nu_{1} = \left. \ \frac{dU}{dy} \right|_{y = 1} = \left. \ \frac{d\theta_{0}}{\text{dy}} \right|_{y = 1} + \varepsilon\left. \ \frac{d\theta_{1}}{\text{dy}} \right|_{y = 1}.\end{align}

With no suction/injection parameter, i. e. \(S \rightarrow 0\), the solution tends to the one given by Eqs. (\ref{e13}) -- (\ref{e23}) of Jha and Aina [22] in the absence of suction/injection parameter. In the following section, Eqs. (\ref{e5}) - (\ref{e7}) are solved numerically for velocity and temperature and the skin friction together with the rate of heat transfer are computed.

4. Numerical solution

The momentum and energy equations given by Eqs. (\ref{e5}) and (\ref{e6}) are solved numerically by using implicit finite difference method. The procedure involves discretization of the transport Eqs. (\ref{e5}) and (\ref{e6}) into the finite difference equations at the grid point \((i , j).\) They are, in order as follows:

\begin{align}\tag{24}\label{e24} \begin{cases} &\frac{U\left( i,j \right) - U\left( i,j - 1 \right)}{\Delta t} + S\frac{U\left( i,j \right) - U\left( i,j - 1 \right)}{\Delta y} = \gamma\left\lbrack \frac{U\left( i + 1,j \right) - 2U\left( i,j \right) + U\left( i - 1,j \right)}{\left( \Delta y \right)^{2}} \right\rbrack - \frac{U\left( i,j \right)}{\text{Da}} + \theta\left( i,j \right),\\ &\frac{\theta\left( i,j \right) - \theta\left( i,j - 1 \right)}{\Delta t} + S\frac{\theta\left( i,j \right) - \theta\left( i,j - 1 \right)}{\Delta y} = \frac{1}{\Pr\frac{k_{m}}{k_{f}}\left\lbrack \frac{\theta\left( i + 1,j \right) - 2\theta\left( i,j \right) + \theta\left( i - 1,j \right)}{\left( \Delta y \right)^{2}} \right\rbrack}.\end{cases}\end{align}

The time derivative is replaced by the backward difference formula, while spatial derivative is replaced by the central difference formula. The above equations are solved by the Thomas algorithm by manipulating into a system of linear algebraic equations in the tridiagonal form. In each time step, the process of numerical integration for every dependent variable starts from the first neighbouring grid point of the plate at \(y = - 1\), using the tridiagonal form of the finite difference Eqs. (\ref{e5}) and (\ref{e6}) until it reaches at immediate grid point of the plate at \(y = 1\). In each time step the temperature field has been solved and then the evaluated values are used to obtain the velocity field. The process of computation is advanced until a steady state is approached by satisfying the following convergence criterion:

\begin{align}\tag{26}\label{e26}\frac{\sum_{}^{}|A_{i,j + 1} - A_{i,j}|}{M|A{|_{\max}}^{- 4}},\end{align}

with respect to the temperature and velocity fields, here, \(A_{i,j}\) stands for the velocity and temperature fields, \(M\) is the number of interior grid points and \(|A|_{\max}\) is the maximum absolute value of\(\text{\ A}_{i,j}\). In the numerical computation, there is a need to specify \(\Delta t\) to get a steady solution as rapidly as possible, yet small enough to avoid instabilities. It is set, which is suitable for the present computation, as \[\Delta t = stabr \times \left( \Delta y \right)^{2}\,.\] The parameter `\(\text{stabr}\)' is determined by numerical experiment in order to achieve convergence and stability of the solution procedure. Numerical experiments show that the value 2 is suitable for numerical computations. In order to confirm the validity of this numerical model, the numerical scheme are compared with analytical solution derived for steady state problem using perturbation technique. At large value of time, the obtained numerical values using implicit finite difference method for velocity, temperature, skin-friction and rate of heat transfer are in excellent agreement with the obtained steady state values using the perturbation method.

5. Results and discussion

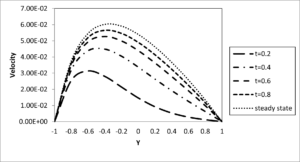
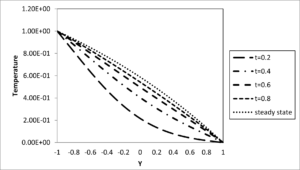
Effect of suction/injection on transient free convective flow in vertical porous channel formed by two infinite vertical porous plates filled with porous material in presence of thermal dispersion has been considered. The basic parameters that governed this flow are the suction/injection parameter \(\left( S \right)\) which were simultaneously applied each to opposite porous plates, Prandtl number \(\left( \Pr() \right)\), which is inversely proportional to the thermal diffusivity of the working fluid, the non-dimensional time \(\left( t \right)\), Darcy number \(\left( \text{Da} \right)\), and thermal dispersion parameter \(\left( C \right)\). For the purpose of discussions, some numerical calculations are carried out for dimensionless velocity, temperature, skin friction and rate of heat transfer. The effects of various parameters on the flow are presented in graphical form in Figures 2--10 so as to clearly reveal the influence of each governing parameter on the flow formation and temperature distribution. In addition, in experimental analysis of air flow through aluminium foam heat exchangers, Calmidi and Mhajan [23] reported a value of \(0.06\) for their \(C\) while their \(\text{Gr}\) (here \(\text{Gr}\) is pore-Reynolds, i.e. square root of permeability is defined as the length scale) was limited to \(135\) with their maximum \(\Pr\)value being \(0.0075\). Note that this \(\Pr\) value is based on effective thermal conductivity rather that of air. This combination leads to a maximum of \(0.061\) for \(C\). Hunt and Tien [24], on the other hand, reported theoretical and experimental analysis of dispersion effects in foams with water as the working fluid leading to \(0.6\) as their maximum \(C\) value. This study has been performed over the reasonable ranges of \(0.01 < Da < 0.1,\) \(0.0 < t < 0.6,\) and \(0.0 < C < 0.5\). The selected reference values of \(Da,t,\) and \(C\) for the present analysis are \(0.1,\) \(0.2,\) and \(0.2,\) respectively as given in Jha and Aina [22]. Furthermore, the value of suction/ injection has been performed over the reasonable ranges of \(- 5 < S < 5\) and the selected reference values of \(S\) for the present analysis is \(0.5\). The effect of time on velocity profile is depicted in Figure 2. It is clearly seen in Figure 2 that, by increasing the non-dimensional time, the fluid velocity increases and finally attains its steady state. This is consequence of temperature increase that results from increase in time, since convection current becomes stronger and hence velocity increases with time.

Figure 2. Velocity profile for different values of time \(\left( S = 0.5,Da = 0.1,C = 0.2,\Pr = 0.71 \right)\)

Figure 3 depicts the role of non-dimensional time \(\left( t \right)\) on the transient temperature profiles. It is reveals that, temperature increases with increase in time and finally attains its steady state.

Figure 3. Temperature profile for different values of time \(\left( S = 0.5,Da = 0.1,C = 0.2,\Pr = 0.71 \right)\)

Figures 4 and 5 describe the influence of Prandtl number on the velocity as well as temperature profile, respectively. It is clearly shows in these Figures that, the fluid velocity and temperature decreases as Prandtl number increases. The physical explanation to this is that, fluids with high Prandtl number have a lower thermal diffusivity and high viscosity, which causes low heat penetration and reduce thermal boundary layer.

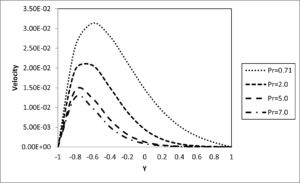
Figure 4. Velocity profile for different values of Prandth number \(\left( S = 0.5,Da = 0.1,C = 0.2,t = 0.2 \right)\)

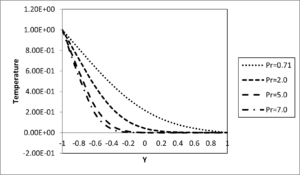
Figure 5. Temperature profile for different values of Prandth number \(\left( S = 0.5,Da = 0.1,C = 0.2,t = 0.2 \right)\)

Figure 6 illustrate the impact of Darcy number on the velocity profile. The velocity is observed to increases as Darcy number increase.

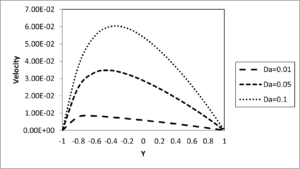
Figure 6. Velocity profile for different values of Darcy number \(\left( S = 0.5,C = 0.2,\Pr = 0.71,t = 0.2 \right)\)

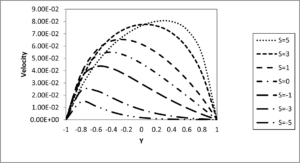
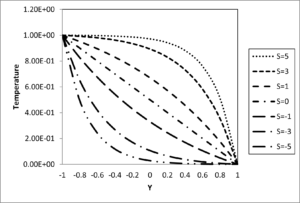
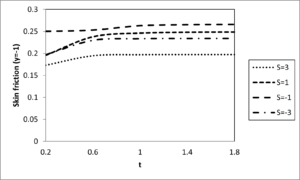
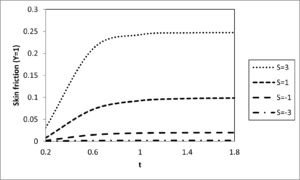
Figures 7 and 8 show the effect of suction/injection parameter \(\left( S \right)\) on the dimensionless temperature and velocity profiles, respectively. In this study, when suction takes place at the plate \(\left( Y = 1 \right)\) with a corresponding injection at the plate\(\left( Y = - 1 \right)\), \(S\)is positive \(\left( S > 0 \right)\). For the reverse phenomenon, \(S\) is negative \(\left( S < 0 \right)\). Both temperature and velocity are seen to increase with an increase in \(S\) for \(\left( S > 0 \right)\) while the reverse case is observed for \(\left( S < 0 \right)\). This is as a result of heated fluid particles being introduced into the porous channel by injection through the porous plate \(\left( Y = - 1 \right)\) while cold fluid particles are removed from the channel by suction through the porous plate \(\left( Y = 1 \right)\) in the case of \(\left( S > 0 \right)\). This increases the temperature thus strengthening the convection current in the channel, which in turn increases the velocity. On the other hand, cold fluid particles are introduced into the channel by injection through the plate \(\left( Y = 1 \right)\) and hot fluid particles are removed from the channel by suction through the plate \(\left( Y = - 1 \right)\) in the case of \(\left( S < 0 \right)\), thus the reverse phenomenon is observed.

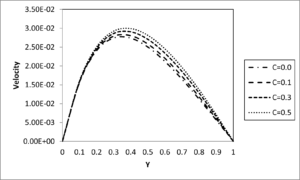
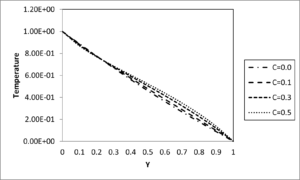
Figures 9 and 10 shown the effect of thermal dispersion parameter\(\left( C \right)\) on the velocity and temperature profiles, respectively.. It is evident from Figures 9 and 10 that, the fluid velocity and temperature increases with the increase in the thermal dispersion parameter. This is physically true because, an increase in thermal dispersion adds more heat to the fluid leading to an increase in temperature, which causes velocity increase. Furthermore, it is interesting to note from these figures that, the impact of thermal dispersion parameter on the fluid velocity and temperature is more pronounced for higher values of Darcy number.

Figure 7. Velocity profile for different values of C \(\left( Da = 0.1,S = 0.5,\Pr = 0.71,t = 0.2 \right)\)

Figure 8. Temperature profile for different values of suction/injection \(\left( C = 0.2,Da = 0.1,\Pr = 0.71,t = 0.2 \right)\)

Figure 9. Velocity profile for different values of C \(\left( Da = 0.1,S = 0.5,\Pr = 0.71,t = 0.2 \right)\)

Figure 10. Temperature profile for different values of C \(\left( Da = 0.1,S = 0.5,\Pr = 0.71,t = 0.2 \right)\)

Figures 11 and 12 presents variation of skin-friction at \(\left( Y = - 1 \right)\) and \(\left( Y = 1 \right)\), respectively, for different values of suction/injection parameter \(\left( S \right)\) and time \(\left( t \right)\). These figures reveal that the skin-friction decreases with increase in suction/injection parameter on the plate \(\left( Y = - 1 \right)\) while the result is reversed on the plate \(\left( Y = 1 \right)\). In addition, the skin-friction is observed to increase with increase in time on both walls.

Figure 11. Effects of suction/injection on the skin friction at \(y = – 1\)

Figure 12. Effects of suction/injection on the skin friction at \(y = 1\)

Figures 13 and 14 displays the variation of rate of heat transfer for different values of suction/injection parameter \(\left( S \right)\) and time \(\left( t \right)\) at \(\left( Y = - 1 \right)\) and \(\left( Y = 1 \right)\), respectively. It is observed that the rate of heat transfer decreases with increase in suction/injection parameter and time at \(\left( Y = - 1 \right)\) and converse is the case at \(\left( Y = 1 \right)\).

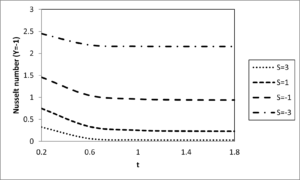
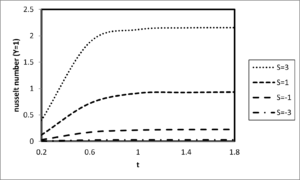
Figure 13. Effects of thermal dispersion on the Nusselt number at \(y = 0\)

Figure 14. Effects of thermal dispersion on the Nusselt number at \(y = 1\)

Finally, in order to see the accuracy of numerical solutions, numerical values of velocity and temperature are presented in Tables 1 and 2, respectively, for steady state operating conditions using perturbation technique and implicit finite difference method for transient mathematical model using large value of time \(\left( t = 2.6 \right)\). An excellent agreement is found between them.

Table 1. Comparison of numerical value of the transient state velocity obtained using the implicit finite difference and the steady state velocity obtained analytically.

	\(\left( kr = 1.0,Pr = 0.71,Gr = 10,C = 0.02,Da = 0.1,t = 2.6,S = 0.5 \right)\)
-1.0	0.00000000	0.00000000
-0.8	0.03736919	0.03738409
-0.6	0.05455357	0.05456949
-0.4	0.06021279	0.06023026
-0.2	0.05915494	0.05917777
0.0	0.05403778	0.05406842
0.2	0.04631642	0.04635419
0.4	0.03676961	0.03681032
0.6	0.02578929	0.02582554
0.8	0.01353415	0.01355659
1.0	0.00000000	0.00000000

Table 2. Comparison of numerical value of the transient state temperature obtained using the implicit finite difference and the steady state Temperature obtained analytically.

	\(\left( kr = 1.0,Pr = 0.71,Gr = 10,C = 0.02,Da = 0.1,t = 2.6,S = 0.5 \right)\)
-1.0	1.0000000	1.0000000
-0.8	0.9287799	0.9285012
-0.6	0.8523538	0.8520535
-0.4	0.7703258	0.7701513
-0.2	0.6822769	0.6823002
0.0	0.5877588	0.5879969
0.2	0.4862910	0.4867157
0.4	0.3773574	0.3778983
0.6	0.2604031	0.2609460
0.8	0.1348313	0.1352132
1.0	0.0000000	0.0000000

6. Conclusions

The effect of suction/injection on transient and steady free convective flow in vertical porous channel formed by two infinite vertical parallel porous plates filled with porous material in the presence of thermal dispersion has been investigated. The temperature field and velocity field are obtained analytically by perturbation method for the steady situation and numerically by implicit finite difference technique for transient situation. The skin-friction and rate of heat transfer expressed as Nusselt number are derived from the velocity and temperature, respectively. Graphical results for the temperature, velocity, skin friction and rate of heat transfer are presented and discussed for various physical parameter values. The main findings are as follows:

The time required to reach steady state velocity and temperature field strongly dependent on Prandtl number, suction/injection parameter and thermal dispersion parameter.
The impact of thermal dispersion parameter on the fluid velocity and temperature is more pronounced for higher values of Darcy number.
The heat transfer is higher at left porous plate \(\left( Y = - 1 \right)\) where injection takes place in comparison to right porous plate where suction takes place \(\left( Y = 1 \right)\).
The introduction of suction/injection has distorted the symmetric nature of the flow formation.
An increase in thermal dispersion parameter and time enhanced the skin friction and rate of heat transfer.

Nomenclature

\(C =\) Dispersion coefficient \(C_{\rho} =\) specific heat of the fluid at constant pressure \(Da =\) Darcy number \(g =\)acceleration due to gravity \(Gr =\) Grashof number \(h =\) gap between the plates \(Nu_{0} =\) Nusselt number at \(\left( Y = - 1 \right)\) \(Nu_{1} =\) Nusselt number at \(\left( Y = 1 \right)\) \(\Pr =\)Prandtl number \(S =\)suction/injection parameter \(t' =\) dimensional time \(t =\) dimensionless time \(T =\)temperature of the fluid \(T_{0} =\) temperature of the fluid and plates in reference state \(\left( t' \leq 0 \right)\) \(u' =\) dimensional velocity of the fluid \(U =\) dimensionless velocity of the fluid \(V_{0} =\)constant suction/injection velocity \(y' =\)dimensional coordinate perpendicular to the channel walls \(y =\) dimensionless coordinate perpendicular to the channel walls

Greek Letters

\(\beta =\) coefficient of thermal expansion \(\gamma =\) ratio of kinematics viscosity \(\theta =\) dimensionless temperature \(\rho =\) density \(\tau_{0} =\)dimensionless skin friction at \(\left( Y = - 1 \right)\) \(\tau_{1} =\) dimensionless skin friction at \(\left( Y = 1 \right)\) \(v =\)fluid kinematic viscosity \(v_{\text{eff}} =\)effective kinematic viscosity \(k =\) thermal conductivity \(k_{m} =\) thermal conductivity of the solid phase \(k_{f} =\) thermal conductivity of the fluid phase

Author Contributions:

All authors contributed equally in this paper. All authors read and approved the final version of this paper.

Conflicts of Interest:

The authors declare no conflict of interest.

References

Vafai, K., & Tien, C. L. (1982). Boundary and inertia effects on convective mass transfer in porous media. International Journal of Heat and Mass Transfer, 25(8), 1183-1190.[Google Scholor]
Srinivasan, V., & Vafai, K. (1994). Analysis of linear encroachment in two-immiscible fluid systems in a porous medium. Journal of Fluids Engineering, 116, 135-139.[Google Scholor]
Jha, B. K., Joseph, S. B., & Ajibade, A. O. (2012). Transient free-convective flow through a vertical porous annulus. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 226(2), 105-116.[Google Scholor]
Sheremet, M. A., Revnic, C., & Pop, I. (2017). Free convection in a porous wavy cavity filled with a nanofluid using Buongiorno's mathematical model with thermal dispersion effect. Applied Mathematics and Computation, 299, 1-15.[Google Scholor]
Umavathi, J. C., Sheremet, M. A., & Mohiuddin, S. (2016). Combined effect of variable viscosity and thermal conductivity on mixed convection flow of a viscous fluid in a vertical channel in the presence of first order chemical reaction. European Journal of Mechanics-B/Fluids, 58, 98-108.[Google Scholor]
Kasaeipoor, A., Malekshah, E. H., & Kolsi, L. (2017). Free convection heat transfer and entropy generation analysis of MWCNT-MgO (15\%- 85\%)/Water nanofluid using Lattice Boltzmann method in cavity with refrigerant solid body-Experimental thermo-physical properties. Powder Technology, 322, 9-23.[Google Scholor]
Rahimi, A., Kasaeipoor, A., & Malekshah, E. H. (2017). Lattice Boltzmann simulation of natural convection and entropy generation in cavities filled with nanofluid in existence of internal rigid bodies-Experimental thermo-physical properties. Journal of Molecular Liquids, 242, 580-593.[Google Scholor]
Rahimi, A., Kasaeipoor, A., & Malekshah, E. H. (2017). Natural convection analysis by entropy generation and heatline visualization using lattice Boltzmann method in nanofluid filled cavity included with internal heaters-Empirical thermo-physical properties. International Journal of Mechanical Sciences, 133, 199-216.[Google Scholor]
Salari, M., Malekshah, E. H., & Esfe, M. H. (2017). Three dimensional simulation of natural convection and entropy generation in an air and MWCNT/water nanofluid filled cuboid as two immiscible fluids with emphasis on the nanofluid height ratio's effects. Journal of Molecular Liquids, 227, 223-233.[Google Scholor]
Malekshah, E. H., & Salari, M. (2017). Experimental and numerical investigation of natural convection in a rectangular cuboid filled by two immiscible fluids. Experimental Thermal and Fluid Science, 85, 388-398.[Google Scholor]
Al-Rashed, A. A., Kolsi, L., Kalidasan, K., Malekshah, E. H., Borjini, M. N., & Kanna, P. R. (2017). Second law analysis of natural convection in a CNT-water nanofluid filled inclined 3D cavity with incorporated Ahmed body. International Journal of Mechanical Sciences, 130, 399-415.[Google Scholor]
Murthy, P. V. S. N., & Singh, P. (1997). Effect of viscous dissipation on a non-Darcy natural convection regime. International Journal of Heat and Mass Transfer, 40(6), 1251-1260.[Google Scholor]
3 Hong, J. T., & Tien, C. (1987). Analysis of thermal dispersion effect on vertical-plate natural convection in porous media. International Journal of Heat and Mass Transfer, 30, 143-150.[Google Scholor]
Shih-Wen, H., Cheng, P., & Chao-Kuang, C. (1992). Non-uniform porosity and thermal dispersion effects on natural convection about a heated horizontal cylinder in an enclosed porous medium. International Journal of Heat and Mass Transfer, 35(12), 3407-3418.[Google Scholor]
Kuznetsov, A. V. (2001). Influence of thermal dispersion on forced convection in a composite parallel-plate channel. Zeitschrift f\"ur Angewandte Mathematik und Physik, 52, 135-150.[Google Scholor]
Amiri, A., & Vafai, K. (1994). Analysis of dispersion effects and non-thermal equilibrium, non-Darcian, variable porosity incompressible flow through porous media. International Journal of Heat and Mass Transfer, 37(6), 939-954.[Google Scholor]
Wakao, N., & Kaguei S. (1996). Heat and Mass Transfer in Packed Beds. Gordon and Breach, New York.[Google Scholor]
Sheremet, M. A., Pop, I., & Bachok, N. (2016). Effect of thermal dispersion on transient natural convection in a wavy-walled porous cavity filled with a nanofluid: Tiwari and Das’ nanofluid model. International Journal of Heat and Mass Transfer, 92, 1053-1060.[Google Scholor]
Jhangeer, A., Faridi, W. A., Asjad, M. I., & Akg\"ul, A. (2021). Analytical study of soliton solutions for an improved perturbed Schrödinger equation with Kerr law non-linearity in non-linear optics by an expansion algorithm. Partial Differential Equations in Applied Mathematics, 4, 100102.[Google Scholor]
Faridi, W. A., Asjad, M. I., & Jhangeer, A. (2021). The fractional analysis of fusion and fission process in plasma physics. Physica Scripta, 96(10), 104008.[Google Scholor]
Asjad, M. I., Faridi, W. A., Jhangeer, A., Abu-Zinadah, H., & Ahmad, H. (2021). The fractional comparative study of the non-linear directional couplers in non-linear optics. Results in Physics, 27, 104459. [Google Scholor]
Jha, B. K., & Aina, B. (2017). Numerical investigation of transient free convective flow in vertical channel filled with porous material in the presence of thermal dispersion. Computational Mathematics and Modeling, 28, 350-367.[Google Scholor]
Calmidi, V. V., & Mahajan, R. L. (2000). Forced convection in high porosity metal foams. Journal of Heat Transfer, 122, 557-565.[Google Scholor]
Hunt, M. L., & Tien, C. L. (1988). Effects of thermal dispersion on forced convection in fibrous media. International Journal of Heat and Mass Transfer, 31(2), 301-309.[Google Scholor]