Engineering and Applied Science Letters
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2018.0001
Some Numerical Invariants Associated with V-phenylenic Nanotube and Nanotori
Rachanna Kanabur\(^1\), Sunilkumar Hosamani
Department of Mathematics, Bldea’s Commerce BHS Arts and TGP Science, College, Jamakhandi – 587301 Karnataka, India; (R.K)
Department of Mathematics, Rani Channamma University Belagavi – 591156 Karnataka, India; (S.H)
\(^{1}\)Corresponding Author; rachukanabur@gmail.com
Abstract
Index Terms:
1. Introduction
Mathematical chemistry is a branch of theoretical chemistry for discussion and prediction of the molecular structure using mathematical methods without necessarily referring to quantum mechanics. Chemical graph theory is a branch of mathematical chemistry which applies graph theory to mathematical modelling of chemical phenomena [1, 2]. This theory had an important effect on the development of the chemical sciences. In mathematics chemistry, a molecular graph is a simple graph such that its vertices correspond to the atoms and the edges to the bonds. And also a connected graph is a graph such that there is a path between all pairs of vertices. Note that hydrogen atoms are often omitted [2]. Let \(G=(V, E)\) be a graph with n vertices and \(m\) edges. The degree of a vertex \(u\in V(G)\) is denoted by \(d_{G}(u)\) and is the number of vertices that are adjacent to \(u\). The edge connecting the vertices \(u\) and \(v\) is denoted by \(uv\) [3].2. Computing the Topological Indices of Certain Nanotubes
In [4, 5, 6], Shigehalli and Kanabur have put forward new degree based topological indices viz. arithmetic-geometric index, \(SK\) index, \(SK_{1}\) index and \(SK_{2}\) index. Which are defined as follows: Let \(G=(V,E)\) be a molecular graph,\(d_{G}(u)\) and , \(d_{G}(v)\) is the degree of the vertex \(u\) and \(v\), then \begin{equation} AG_{1}=\sum\limits_{uv\in E(G)}\frac{1}{2\sqrt{d_{u}+d_{v}}}, \end{equation} \begin{equation} SK=\sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2}, \end{equation} \begin{equation} SK_{1}=\sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{2}, \end{equation} \begin{equation} SK_{2}=\sum\limits_{uv\in E(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}. \end{equation} where \(d_{G}(u)\) and \(d_{G}(v)\) are the degrees of the vertices \(u\) and \(v\) in \(G\). In this paper we give explicit formulae for these topological indices of [n]-phenylenic, lattice of \(C_{4}C_{6}C_{8}[m, n]\), \(TUC_{4}C_{6}C_{8}[m, n]\) nanotube, \(C_{4}C_{6}C_{8}[m, n]\) nanotori [7, 8].3. Main Results
The aim of this section, at first, is to compute some topological indices of the molecular graph of linear[n]-phenylenic as depicted in Fig.1Figure 1. The molecular graph of a linear [n]-phenylenic.
Table 1. The number of three types of edges of the graph \(T\)
| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,2)\) | \(6\) |
| \((2,3)\) | \(4n-4)\) |
| \((3,3)\) | \(4n-4\) |
Theorem 3.1. Consider the graph \(T\) of a linear[n]-phenylenic. Then the \(AG_{1}\) , \(SK\), \(SK_{1}\) and \(SK_{2}\) indices of \(T\) are equal to
- \(AG_{1}(G)=8.08n-2.08\),
- \(SK(G)= 22n -10\),
- \(SK_{1}(G)=30n-18\),
- \(SK_{2}(G)=61n-37\).
Proof. 1. \begin{eqnarray*} AG_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=&|E_{1}(G)|\frac{2+2}{2\sqrt{2.2}}+|E_{2}(G)|\frac{2+3}{2\sqrt{2.3}}\\ &&+|E_{3}(G)|\frac{3+3}{2\sqrt{3.3}}\\ &=& 6(1)+(4n-4)\left(\frac{5}{2\sqrt{6}}\right)+(4n-4)(1)\\ &=&8.08n-2.08. \end{eqnarray*} 2. \begin{eqnarray*} SK(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}+d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2+2}{2}+|E_{2}(G)|\frac{2+3}{2}\\ &&+|E_{3}(G)|\frac{3+3}{2}\\ &=&12+10n-10+ 12n-12\\ &=&22n -10. \end{eqnarray*} 3. \begin{eqnarray*} SK_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}d_{v}}{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2.2}{2}+|E_{2}(G)|\frac{2.3}{2}\\ &&+|E_{3}(G)|\frac{3.3}{2}\\ &=&=12+12n-12+ 18n-18\\ &=&30n-18. \end{eqnarray*} 4. \begin{eqnarray*} SK_{2}(G)&=& \sum\limits_{uv\in E(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}+\sum\limits_{uv\in E_{2}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=&|E_{1}(G)|\left(\frac{2+2}{2}\right)^{2}+|E_{2}(G)|\left(\frac{2+3}{2}\right)^{2}\\ &&+|E_{3}(G)|\left(\frac{3+3}{2}\right)^{2}\\ &=&24+25n-25+ 36n-36\\ &=&61n-37. \end{eqnarray*}
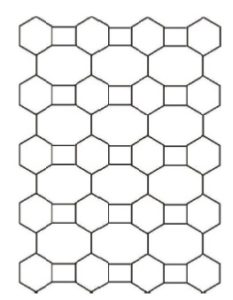
In continue of this section, we see the following figuresFigure 2. The 2-D graph lattice of \(C_{4}C_{6}C_{8}[4,5]\) nanotube
Table 1. The number of three types of edges of the graph \(T\)
| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,2)\) | \(2n+4\) |
| \((2,3)\) | \(4m+4n-8\) |
| \((3,3)\) | \(9mn-8n-5m+4\) |
Theorem 3.2. Consider the graph \(T\) of a linear[n]-phenylenic. Then the \(AG_{1}\), \(SK,\) \(SK_{1}\) and \(SK_{2}\) indices of \(T\) are equal to
- \(AG_{1}(G)=(9n-5.92)m-9.92n-3.84\),
- \(SK(G)= (27n-5)m-10n\),
- \(SK_{1}(G)=(40.5n-10)m-20n+2\),
- \(SK_{2}(G)=(81n-20)m-39n-48\).
Proof. 1. \begin{eqnarray*} AG_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=&|E_{1}(G)|\frac{2+2}{2\sqrt{2.2}}+|E_{2}(G)|\frac{2+3}{2\sqrt{2.3}}\\ &&+|E_{3}(G)|\frac{3+3}{2\sqrt{3.3}}\\ &=& 9mn-5.92m-9.92n-3.04\\ &=&=(9n-5.92)m-9.92n-3.84. \end{eqnarray*} 2. \begin{eqnarray*} SK(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}+d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2+2}{2}+|E_{2}(G)|\frac{2+3}{2}\\ &&+|E_{3}(G)|\frac{3+3}{2}\\ &=&= 4n+8+10m+10n-20+27mn-24n-15m+12\\ &=&27mn-10n-5m. \end{eqnarray*} 3. \begin{eqnarray*} SK_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}d_{v}}{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\frac{d_{u}d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2.2}{2}+|E_{2}(G)|\frac{2.3}{2}\\ &&+|E_{3}(G)|\frac{3.3}{2}\\ &=&=4n+8+12m+12n-24+40.5mn-36n-22.5m+8\\ &=&(40.5n-10)m-20n+2. \end{eqnarray*} 4. \begin{eqnarray*} SK_{2}(G)&=& \sum\limits_{uv\in E(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}+\sum\limits_{uv\in E_{2}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &&+\sum\limits_{uv\in E_{3}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=&|E_{1}(G)|\left(\frac{2+2}{2}\right)^{2}+|E_{2}(G)|\left(\frac{2+3}{2}\right)^{2}\\ &&+|E_{3}(G)|\left(\frac{3+3}{2}\right)^{2}\\ &=&8n+16+25m+25n-100+81mn-72n-45m+36\\ &=&(81n-20)m-39n-48. \end{eqnarray*}
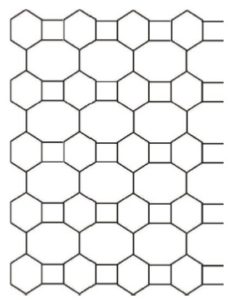
Figure 3. The 2-D graph lattice of \(TUC_{4}C_{6}C_{8}[4,5]\) nanotube.
Table 3. The number of three types of edges of the graph \(T\).
| \((d_{u}, d_{v})\) | Number of edges |
|---|---|
| \((2,3)\) | \(4n\) |
| \((3,3)\) | \(9mn-5m\) |
Theorem 3.3. Consider the graph \(T\) of a linear[n]-phenylenic. Then the \(AG_{1}\), \(SK,\) \(SK_{1}\) and \(SK_{2}\) indices of $T$ are equal to
- \(AG_{1}(G)=(9n-0.92)m\),
- \(SK(G)=(27n-5) m\),
- \(SK_{1}(G)=(40.5n-10.5)m\),
- \(SK_{2}(G)=(81n-20)m.\)
Proof. 1. \begin{eqnarray*} AG_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2\sqrt{d_{u}.d_{v}}}\\ &=&|E_{1}(G)|\frac{2+3}{2\sqrt{2.2}}+|E_{2}(G)|\frac{3+3}{2\sqrt{2.3}}\\ &=& 9mn-5m+4.08m\\ &=&(9n-0.92)m. \end{eqnarray*} 2. \begin{eqnarray*} SK(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}+d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}+d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}+d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2+3}{2}+|E_{2}(G)|\frac{3+3}{2}\\ &=&10m+27mn-15m\\ &=&(27n-5) m. \end{eqnarray*} 3. \begin{eqnarray*} SK_{1}(G)&=& \sum\limits_{uv\in E(G)}\frac{d_{u}d_{v}}{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\frac{d_{u}d_{v}}{2}+\sum\limits_{uv\in E_{2}(G)}\frac{d_{u}d_{v}}{2}\\ &=&|E_{1}(G)|\frac{2.3}{2}+|E_{2}(G)|\frac{3.3}{2}\\ &=&=12mn+(9mn-5m)(4.5)\\ &=&(40.5n-10.5)m. \end{eqnarray*} 4. \begin{eqnarray*} SK_{2}(G)&=& \sum\limits_{uv\in E(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=& \sum\limits_{uv\in E_{1}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}+\sum\limits_{uv\in E_{2}(G)}\left(\frac{d_{u}+d_{v}}{2}\right)^{2}\\ &=&|E_{1}(G)|\left(\frac{2+3}{2}\right)^{2}+|E_{2}(G)|\left(\frac{3+3}{2}\right)^{2}\\ &=&25m+81mn-45m\\ &=&(81n-20) m. \end{eqnarray*}
4. conclusion
In this paper, we have computed the value of \(AG_{1}\) index, \(SK\) index, \(SK_{1}\) index and \(SK_{2}\) index for Linear [n]-phenylenic, lattice of \(C_{4}C_{6}C_{8}[m,n]\), \(TUC_{4}C_{6}C_{8}[m,n]\) nanotube, \(C_{4}C_{6}C_{8}[m,n]\) nanotori without using computer.Competing Interests
The authors declare that they have no competing interests.References
- Diudea, M. V., Gutman, I., & Jantschi, L. (2001). Molecular topology . Huntington, NY: Nova Science Publishers. [Google Scholor]
- Trinajstić, N. (1992). Chemical Graph Theory. CRC Press. Boca Raton. [Google Scholor]
- Harary, F. (1969). Graph theory. Addison-Wesely, Reading mass . [Google Scholor]
- Shigehalli, V. S., & Kanabur, R. (2016). New Version of Degree-Based Topological Indices of Certain nanotube. J. Math. Nanosci , 6(1), 29-42. [Google Scholor]
- Shigehalli, V. S., & Kanabur, R. (2016). Computation of new degree-based topological indices of graphene. Journal of Mathematics, 2016. [Google Scholor]
- Shigehalli, V., & Kanabur, R. (2016). Computing degree-based topological indices of Polyhex nanotubes. Journal of Mathematical Nanoscience, 6(1-2), 47-55. [Google Scholor]
- Nikmehr, M. J., Veylaki, M., & Soleimani, N. (2015). Some topological indices of V-Phenylenic nanotube and nanotori. Optoelectron. Adv. Mater.-Rapid Comm , 9(9), 1147-1149. [Google Scholor]
- Hosamani, S. M., & Gutman, I. (2014). Zagreb indices of transformation graphs and total transformation graphs. Applied Mathematics and Computation , 247, 1156-1160. [Google Scholor]