Engineering and Applied Science Letter
ISSN: 2617-9709 (Online) 2617-9695 (Print)
DOI: 10.30538/psrp-easl2019.0025
Determination of the dynamic shearing force and bending moment of a tensioned single-walled carbon nanotube subjected to a uniformly distributed external pressure
A. A. Yinusa\(^1\), M. G. Sobamowo, A. O. Adelaja
Department of Mechanical Engineering, University of Lagos, Akoka, Lagos, Nigeria.; (A.A.Y & M.G.S & A.O.A)
Abstract
Keywords:
1. Introduction
Since the discovery of CNT by Iijima [1], a considerable number of studies on carbon nanotubes with multi branched arrangements have been analyzed [2, 3, 4]. Subsequently, it has been established that such structures have merits when applied to the functionability of transistors and diodes. As a result, logical investigations and analysis of carbon nanotube have been a subject of interest such as the vibrations of a micro-resonator that is excited by electrostatic and piezoelectric actuations. Studies have been performed on beams, CNT, nano-wires, nano-rods and nano-beam so as to specifically understand and achieve their area of best fit. In achieving this, the well known beam models were employed and dynamic ranges were obtained in the scope of the structures [5, 6, 7, 8]. Different studies have been performed to determine the resonance point and to enhance the mechanical properties of single and multi-walled nanotubes, using initial stress and compressive axial loading, to study the non-coaxial resonance [9, 10, 11, 12, 13, 14]. Elishakoff et al., [15] performed an investigation on the fundamental natural frequencies of double-walled carbon nanotubes and ascertained some stability criteria using some controlling parameters. Mass detection with nonlinear nano-mechanical resonator as well as dynamic range of nanotube- and nanowire-based electromechanical systems have also been studied [16, 17].
In order to be able to predict the dynamic behaviour of embedded carbon nanotubes, Fu et al.[18] and Xu et al. [19] performed some analysis of nonlinear vibration for embedded carbon nanotubes. In application to electrical and electronics, the static and dynamic analysis of carbon nanotube-based switches, micro-resonator under piezoelectric and electrostatic actuations have been presented [20, 21, 22]. As a continuation of the tremendous work, Abdel-Rahman and Nayfeh [23], Hawwa and Al-Qahatani [24] and, Hajnayeb and Khadem [25] performed vibration and instability studies of double wall carbon natotube (DWCNT) using a nonlinear model and considering electrostatic actuation as external excitation agent. In their investigation, DWCNT was situated and conditioned to direct and alternating voltages and different behaviors of the nanotubes were recorded as the exciting agent was varied. They went further to determine the bifurcation point of the DWCNT and concluded that both walls had the same frequency of vibration under the two resonant conditions considered. Belhadj et al. [26] presented their work on a pinned-pinned supported SWCNT employing nonlocal theory of elasticity and obtained natural frequency up to the third mode. They also explained how the high frequency obtained in their work might be harnessed to be of high merit in optical applications. Lei et al. [27] studied the dynamic behaviour of DWCNT by employing the well-known Timoshenko beam theory. The nonlinear governing equations obtained by Sharabiani and Yazdi [28] were applied to nanobeams that were graded and had surface roughness. Wang [29] obtained a closed form model for the aforementioned surface roughness effect for an unforced fluid conveying nanotube and beams based on nonlocal theory of elasticity and ascertained the significance of stability analysis for reasonably small thickness of the tube considered.
Interesting foundation studies have been considered after modelling of CNTs as structures resting on or embedded in elastic foundations such as Winkler, Pasternak and Visco-Pasternak media [30, 31, 32, 33, 34, 35]. Other interesting works through modelling and experiment have also been presented to justify the widespread application of SWCNTs [36, 37, 38, 39, 40, 41]. To the best of the authors' knowledge, no work has been done to dynamically determine the shearing force and bending moment diagram of a tensioned and pressurized SWCNT. Motivated by these considerations, this work aims to dynamically determine the response, shearing force and bending moment of a tensioned SWCNT under an external uniform pressure by employing Integral transform techniques.
2. Problem description and governing equation
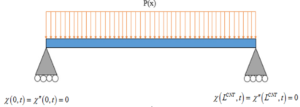
Consider a SWCNT with a uniformly distributed surface pressure as shown in Figure 1. The assumptions used for the analysis include:- the SWCNT is modeled according to Euler-Bernoulli beam
- the exciting agent is a uniform pressure distribution at the SWCNT surface governed by:
\begin{align}\label{equ1} P(x) = \mu A^{CNT} \frac{d}{dx}\left( P_{0} \left( 1 + \frac{\delta}{L^{CNT}}x \right) \right) \end{align}(1)
- the SWCNT is simply supported at both ends.
\begin{align}\label{equ2} \chi(0, t) = \chi^{"}(0, t) = 0 \\ \notag \chi (L^{CNT}, t) = \chi^{"} (L^{CNT}, t ) = 0 \end{align}(2)
- CNT is homogenous and have constant properties.
- CNT have constant cross-section, hence constant moment of Inertia.
Figure 1. Schematic of the SWCNT with Static and Moving uniformly distributed pressure at the surfaces.
3. Methods of solution using integral transforms
Since the resulting model in Equation (4) contains both spatial and temporal part, a superb approach of applying Laplace transform to the temporal and Fourier transform to the spatial terms is adopted. In this present study, the linear transient model in Equation (3) will be solved exactly using Integral transform.3.1. Basic principle of the integral transforms
Fourier transforms can be used to transform second and higher-order spatial derivatives. Although, the inversion of Fourier transform is usually easier than the inversion of Laplace transform, there are some functions which do not have Fourier transform as they have in Laplace transform. Fourier transform could be used to solve problems in.- Finite domains \((0 \leq x \leq L)\)
- Semi-infinite domain, and \(( 0 \leq x \leq \infty, -\infty \leq x \leq 0)\)
- Infinite domains unlike Laplace transform \((-\infty \leq x \leq \infty )\)
Method of solution: Laplace and Fourier transform
Recall that the linear transient governing equation as shown in Equation (4) may be expressed asDetermination of the natural frequency
From Equation (13), the denominator may be arranged to take the form:3.4. Determination of the SWCNT Bending moment and Shear force
The bending moment is related to the SWCNT deflection by [39]:4. Results and Discussion
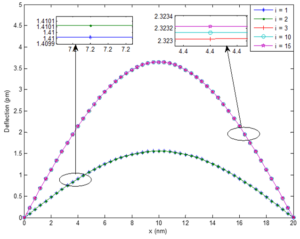
Figure 2 depicts the convergence criteria based on the number of iteration \((i)\) in the close form solution for the deflection of the simply supported SWCNT. The computational time associated with each iteration is shown in Table 1. It is clear that at \(i = 3\), the solution has already converged, hence, extending the iteration above three will only increase the computational time and cost with negligible effect on the improvement of the established solution.Figure 2. Convergence criteria
Table 1. Convergence criteria based on the number of iteration \((i)\) in the close form solution for the deflection of the SWCNT.
| Iteration | Maximum deflection | Computational time (secs) | |||
|---|---|---|---|---|---|
| \(i\) | \(chi (pm)\) | \(n =1\) | \(n = 2\) | \(n =3\) | \(n = 4\) |
| 1 | 1.600 | 0.256784 | 0.323885 | 0.435583 | 0.436961 |
| 2 | 1.601 | 0.296788 | 0.323900 | 0.436781 | 0.446962 |
| 3 | 3.700 | 0.456733 | 0.466385 | 0.468551 | 0.486001 |
| 10 | 3.700 | 1.236734 | 1.523877 | 1.835101 | 1.999921 |
| 15 | 3.700 | 3.456780 | 3.723335 | 3.935513 | 4.001610 |
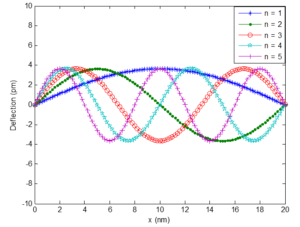
4.1. Effect of the modal number on the deflection of the SWCNT
Figure 3 displays the simply supported SWCNT deflection along its length for the first five mode shapes. Critical visualization shows that as the modal number associated with the kernel that defines the boundary condition increases, the stability of the SWCNT under study decreases as a result of an increase in the cycles covered by the SWCNT for the same length. These occur because the kernel depends on the modal number.Figure 3. SWCNT modes with pinned-pinned condition
4.2. Dynamic response of the SWCNT
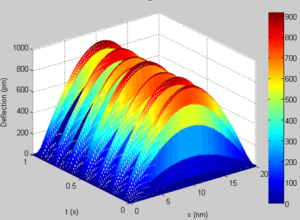
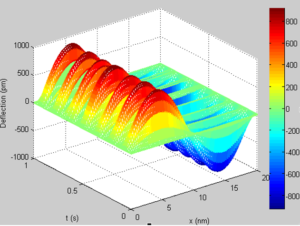
Figure 4, 5, 6, 7 depict the three dimensional dynamic response associated with the SWCNT for the first four modes. As the mode number increases, the number of cycles completed as shown by the dynamic behaviour of the system increases. A critical assessment shows that it is possible to track the behaviour of the CNT at any instance. The dynamic analysis is important as it helps in the quick monitory and adjustment of the CNT during application.Figure 4. Dynamic response of the SWCNT for mode 1
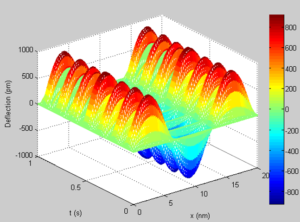
Figure 5. Dynamic response of the SWCNT for mode 2
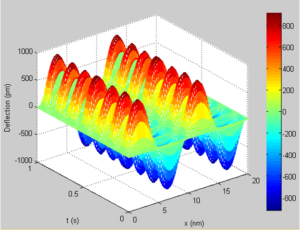
Figure 6. Dynamic response of the SWCNT for mode 3
Figure 7. Dynamic response of the SWCNT for mode 4
Table 2. Comparison of present study with Coskun et al. [1]40} exact method for pinned - pinned condition.
| Mode shape | ||
|---|---|---|
| Mode | Coskun et al. [1] | Present study |
| 1 | 3.14159265 | 3.14159265 |
| 2 | 6.28318531 | 6.28318531 |
| 3 | 9.42477796 | 9.42477796 |
| 4 | - | 12.56637061 |
| 5 | - | 15.70796327 |
4.3. Effect of modal number and length on the frequency of the SWCNT
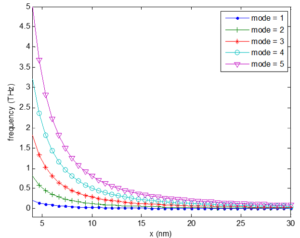
Figure 8 depicts the influence of modal number and length on the frequency of the SWCNT. A careful study helps visualizes the effect of these two important parameters on stability of the SWCNT. The frequency of SWCNT which is a vital parameter in the study of the SWCNT stability reaches some THz and continues to increase as the modal number increases. This astonishing property enables SWCNT to offer exceptional optical and mechanical properties although there is always need to dampen the frequency to an application limit. These two parameters as a result of their tremendous effects on frequency may be used to annul the effect on each other when one of them is desired based on the requirement of the engineering design and applications.Figure 8. Effect of modal number on the frequency
Table 3. Comparison of the present study with exact solution of Belhadj et al. [26] for pinned - pinned condition for the frequency of the SWCNT (THz).
| Length (nm) | Belhadj et al.[26] | Present study | ||||
|---|---|---|---|---|---|---|
| Mode 1 | Mode 2 | Mode 3 | Mode 1 | Mode 2 | Mode 3 | |
| 1 | 0.3 | 1.0 | 2.5 | 0.3 | 1.0 | 2.5 |
| 2 | 0.2 | 0.6 | 1.6 | 0.2 | 0.6 | 1.6 |
| 3 | 0.2 | 0.4 | 0.7 | 0.2 | 0.4 | 0.7 |
| 4 | 0.2 | 0.3 | 0.5 | 0.2 | 0.3 | 0.5 |
| 5 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 | 0.2 |
4.4. The Shear force and bending moment of the SWCNT
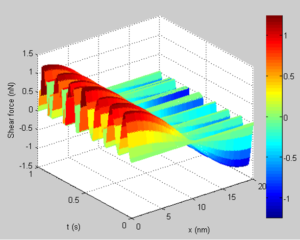
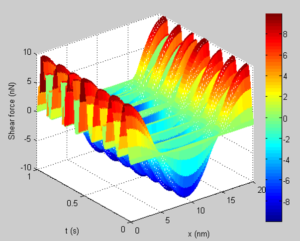
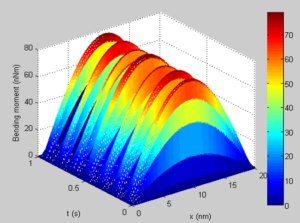
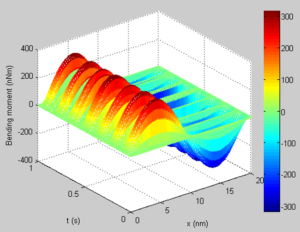
Figure 9, 10, 11, 12 depict the three dimensional Shear force and bending moment diagram of the SWCNT for the first two modes. A critical assessment shows that it is possible to track the positions of maximum shear and maximum moment for proper design of the CNT device. The dynamic analysis is important as it helps in the quick monitory and adjustment of the CNT during application.Figure 9. Shear force Diagram of the SWCNT for mode 1
Figure 10. Shear force Diagram of the SWCN for mode 2
Figure 11. Bending moment Diagram of the SWCNT for mode 1
Figure 12. Bending moment Diagram of the SWCNT for mode 2
5. Conclusion
In this paper, analytical investigations of dynamic response of a SWCNT subjected to an external uniform pressure have been carried out using Integral transform. The exact solution as presented in the present study was reduced to the model of Coskun et al. [40] beam model and a very good agreement was obtained. The natural frequency as obtained in this study was also reduced to the model of Belhadj et al. [26] and an excellent agreement was reached. It was established that the Integral transform gave a good result and was efficient for the problem investigated. Also, some necessary parametric studies were performed to fully understand the dynamic behaviour of SWCNTs and to justify the widespread application of SWCNTs subjected to a uniformly distributed pressure acting externally. Furthermore, the dynamic study reveals that a point of maximum shear force on the CNT produces the minimum bending moment at any mode and for any parameter value considered. It is envisaged that this work will enhance the use of SWCNT under the influence of uniform surface pressure to structural, electrical and mechanical applications.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflicts of Interest:
The authors declare no conflict of interest.References
- Iijima, S. (1991). Helical microtubules of graphitic carbon. Nature, 354(6348), 56. [Google Scholor]
- Terrones, M., Banhart, F., Grobert, N., Charlier, J. C., Terrones, H., & Ajayan, P. M. (2002). Molecular junctions by joining single-walled carbon nanotubes. Physical review letters, 89(7), 075505.[Google Scholor]
- Nagy, P., Ehlich, R., Biro, L. P., & Gyulai, J. (2000). Y-branching of single walled carbon nanotubes. Applied Physics A, 70(4), 481-483. [Google Scholor]
- Chernozatonskii, L. A. (1992). Carbon nanotube connectors and planar jungle gyms. Physics Letters A, 172(3), 173-176. [Google Scholor]
- Liew, K. M., Wong, C. H., He, X. Q., Tan, M. J., & Meguid, S. A. (2004). Nanomechanics of single and multiwalled carbon nanotubes. Physical review B, 69(11), 115429. [Google Scholor]
- Pantano, A., Boyce, M. C., & Parks, D. M. (2004). Mechanics of axial compression of single and multi-wall carbon nanotubes. Journal of engineering materials and technology, 126(3), 279-284.[Google Scholor]
- Pantano, A., Parks, D. M., & Boyce, M. C. (2004). Mechanics of deformation of single-and multi-wall carbon nanotubes. Journal of the Mechanics and Physics of Solids, 52(4), 789-821. [Google Scholor]
- Qian, D., Wagner, G. J., Liu, W. K., Yu, M. F., & Ruoff, R. S. (2002). Mechanics of carbon nanotubes. Applied mechanics reviews, 55(6), 495-533. [Google Scholor]
- Salvetat, J. P., Bonard, J. M., Thomson, N. H., Kulik, A. J., Forro, L., Benoit, W., & Zuppiroli, L. (1999). Mechanical properties of carbon nanotubes. Applied Physics A, 69(3), 255-260.[Google Scholor]
- Yinusa, A., & Sobamowo, G. (2019). Analysis of Dynamic Behaviour of a Tensioned Carbon Nanotube in Thermal and Pressurized Environments. Karbala International Journal of Modern Science, 5(1), 2. [Google Scholor]
- Yoon, J., Ru, C. Q., & Mioduchowski, A. (2002). Noncoaxial resonance of an isolated multiwall carbon nanotube. Physical Review B, 66(23), 233402. [Google Scholor]
- Wang, X., & Cai, H. (2006). Effects of initial stress on non-coaxial resonance of multi-wall carbon nanotubes. Acta materialia, 54(8), 2067-2074. [Google Scholor]
- Wang, C. M., Tan, V. B. C., & Zhang, Y. Y. (2006). Timoshenko beam model for vibration analysis of multi-walled carbon nanotubes. Journal of Sound and Vibration, 294(4-5), 1060-1072. [Google Scholor]
- Zhang, Y., Liu, G., & Han, X. (2005). Transverse vibrations of double-walled carbon nanotubes under compressive axial load. Physics Letters A, 340(1-4), 258-266. [Google Scholor]
- Elishakoff, I., & Pentaras, D. (2009). Fundamental natural frequencies of double-walled carbon nanotubes. Journal of Sound and Vibration, 322(4-5), 652-664. [Google Scholor]
- Buks, E., & Yurke, B. (2006). Mass detection with a nonlinear nanomechanical resonator. Physical Review E, 74(4), 046619. [Google Scholor]
- Postma, H. C., Kozinsky, I., Husain, A., & Roukes, M. L. (2005). Dynamic range of nanotube-and nanowire-based electromechanical systems. Applied Physics Letters, 86(22), 223105.[Google Scholor]
- Fu, Y. M., Hong, J. W., & Wang, X. Q. (2006). Analysis of nonlinear vibration for embedded carbon nanotubes. Journal of Sound and Vibration, 296(4-5), 746-756. [Google Scholor]
- Xu, K. Y., Guo, X. N., & Ru, C. Q. (2006). Vibration of a double-walled carbon nanotube aroused by nonlinear intertube van der Waals forces. Journal of Applied Physics, 99(6), 064303.[Google Scholor]
- Dequesnes, M., Tang, Z., & Aluru, N. R. (2004). Static and dynamic analysis of carbon nanotube-based switches. Journal of engineering materials and technology, 126(3), 230-237. [Google Scholor]
- Ouakad, H. M., & Younis, M. I. (2010). Nonlinear dynamics of electrically actuated carbon nanotube resonators. Journal of computational and nonlinear dynamics, 5(1), 011009. [Google Scholor]
- Zamanian, M., Khadem, S. E., & Mahmoodi, S. N. (2009). Analysis of non-linear vibrations of a microresonator under piezoelectric and electrostatic actuations. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 223(2), 329-344. [Google Scholor]
- Abdel-Rahman, E. M., & Nayfeh, A. H. (2003). Secondary resonances of electrically actuated resonant microsensors. Journal of Micromechanics and Microengineering, 13(3), 491. [Google Scholor]
- Hawwa, M. A., & Al-Qahtani, H. M. (2010). Nonlinear oscillations of a double-walled carbon nanotube. Computational Materials Science, 48(1), 140-143. [Google Scholor]
- Hajnayeb, A., & Khadem, S. E. (2012). Nonlinear vibration and stability analysis of a double-walled carbon nanotube under electrostatic actuation. Journal of Sound and Vibration, 331(10), 2443-2456.[Google Scholor]
- Belhadj, A., Boukhalfa, A., & Belalia, S. A. (2017). Carbon Nanotube Structure Vibration Based on Non-local Elasticity. Journal of Modern Materials, 3(1), 9-13. [Google Scholor]
- Lei, X. W., Natsuki, T., Shi, J. X., & Ni, Q. Q. (2012). Surface effects on the vibrational frequency of double-walled carbon nanotubes using the nonlocal Timoshenko beam model. Composites Part B: Engineering, 43(1), 64-69. [Google Scholor]
- Sharabiani, P. A., & Yazdi, M. R. H. (2013). Nonlinear free vibrations of functionally graded nanobeams with surface effects. Composites Part B: Engineering, 45(1), 581-586. [Google Scholor]
- Wang, L. (2010). Vibration analysis of fluid-conveying nanotubes with consideration of surface effects. Physica E: Low-dimensional Systems and Nanostructures, 43(1), 437-439. [Google Scholor]
- Biro, L. P., Horvath, Z. E., Mark, G. I., Osvath, Z., Koos, A. A., Benito, A. M., ... & Lambin, P. (2004). Carbon nanotube Y junctions: growth and properties. Diamond and related materials, 13(2), 241-249. [Google Scholor]
- Lin, R. M. (2012). Nanoscale vibration characterization of multi-layered graphene sheets embedded in an elastic medium. Computational Materials Science, 53(1), 44-52. [Google Scholor]
- Pradhan, S. C., & Phadikar, J. K. (2009). Small scale effect on vibration of embedded multilayered graphene sheets based on nonlocal continuum models. Physics letters A, 373(11), 1062-1069. [Google Scholor]
- Arani, A. G., Zarei, M. S., Amir, S., & Maraghi, Z. K. (2013). Nonlinear nonlocal vibration of embedded DWCNT conveying fluid using shell model. Physica B: Condensed Matter, 410, 188-196. [Google Scholor]
- Arani, A. G., & Amir, S. (2013). Electro-thermal vibration of visco-elastically coupled BNNT systems conveying fluid embedded on elastic foundation via strain gradient theory. Physica B: Condensed Matter, 419, 1-6. [Google Scholor]
- Eichler, A., Moser, J., Chaste, J., Zdrojek, M., Wilson-Rae, I., & Bachtold, A. (2011). Nonlinear damping in mechanical resonators made from carbon nanotubes and graphene. Nature nanotechnology, 6(6), 339. [Google Scholor]
- Housner, G. W., Dodds, H. L., & Runyan, H. (1965). Effect of High Velocity Fluid flow in the Bending Vibrations and static Divergence of Simply Supported Pipes. National Aeronautics and Space Administration Report NASA TN D-2870. [Google Scholor]
- Sobamowo, M. G. (2017). Nonlinear thermal and flow-induced vibration analysis of fluid-conveying carbon nanotube resting on Winkler and Pasternak foundations. Thermal Science and Engineering Progress, 4, 133-149. [Google Scholor]
- Liu, F., Wagterveld, R. M., Gebben, B., Otto, M. J., Biesheuvel, P. M., & Hamelers, H. V. M. (2014). Carbon nanotube yarns as strong flexible conductive capacitive electrodes. Colloid and Interface Science Communications, 3, 9-12. [Google Scholor]
- Sobamowo, M. G., & Yinusa, A. A. (2018). Thermo-fluidic parameters effects on nonlinear vibration of fluid-conveying nanotube resting on elastic foundations using homotopy perturbation method. J Therm Eng, 4(4), 2211-2233. [Google Scholor]
- Coskun, S. B., Atay, M. T., & Ozturk, B. (2011). Transverse vibration analysis of Euler-Bernoulli beams using analytical approximate techniques. Advances in Vibration Analysis Research, 1-22. [Google Scholor]
- Sobamowo, M. G., & Yinusa, A. A. (2017). Power Series-Aftertreatment Technique for Nonlinear Cubic Duffing and Double-Well Duffing Oscillators. Journal of Computational Applied Mechanics, 48(2), 297-306. [Google Scholor]