On edge-prime cubic graphs with small components

1. Introduction

Let $G=(V(G),E(G))$ (or $G=(V,E)$ for short if not ambiguous) be a simple, finite and undirected $(p,q)$-graph of order $|V|=p$ and size $|E| = q$. For integers $a,b$ with $a\le b$, let $[a,b]=\{n\in Z \,|\, a\le n\le b\}$. All notation not defined in this paper can be found in [1].

The concept of prime labeling was originated by Entringer and it was introduced in a paper by Tout et al. [2]. A graph $G$ with $p$ vertices and $q$ edges is said to have a prime labeling if function $f : V \to [1,p]$ is bijective and for every edge $e = uv$ of $G$, $GCD(f(u), f(v)) = 1$. For simplicity, we will use $(a,b)$ to denote $GCD(a,b)$. Currently, the two most prominent open conjectures involving prime labelings are the following:

1. All tree graphs have a prime labeling (Entringer-Tout Conjecture);
2. All unicyclic graphs have a prime labeling (Seoud and Youssef [3]).

In 2011, Haxell and Pikhurko [4] proved that all large trees are prime. In 1991, Deretsky et al. [5] introduced the notion of dual of prime labeling which is known as vertex prime labeling. A graph with $q$ edges has vertex prime labeling if its edges can be labeled with distinct integers $[1,q]$ such that for each vertex of degree at least 2, the greatest common divisor of the labels on its incident edges is 1. A conjecture: Any 2-regular graph has a vertex prime labeling if and only if it does not have two odd cycles." was proposed.

An excellent survey on graph labeling is maintained by Gallian [6]. In [7], we introduce another prime labeling of graphs.

Definition 1. Let $G= (V,E)$ be a $(p,q)$-graph. A bijection $f: E \to [1,q]$ is called an edge-prime labeling if for each edge $uv$ in $E$, we have $(f^+(u),f^+(v))=1$, where $f^+(u) = \sum_{uw\in E} f(uw)$. A graph that admits an edge-prime labeling is called an edge-prime graph.

Among others, we proved that all 2-regular graphs, complete bipartite graphs $K(2,n)$, the bipartite graph $K(2,n)+ K(2,n)$ $(n\ge 2)$, disjoint union of paths with at most one $P_2$ component, the generalized theta graph having $n\ge 3$ internally disjoint paths of length 3 (respectively, 4), or having 3 internally disjoint paths of length $n\ge 2$ and certain family of trees are edge-prime. It is a conjecture that all trees of diameter at least 3 are edge-prime.

Let $n(G)$ (or $nG$ if no ambiguity) denote the disjoint union of $n$ copies of graph $G$. In this paper we obtained some sufficient conditions for graphs with regular component(s) to admit or not admit an edge-prime labeling. Consequently, we proved that if $G$ is a cubic graph with every component is of order $4, 6$ or $8$, then $G$ is edge-prime if and only if $G\not\cong K_4$ or $nK(3,3)$, $n\equiv2,3\pmod{4}$. In what follows, we only consider cubic graphs unless specified otherwise.

It is clear that an edge labeling $f: E(G)\to [1,|E(G)|]$ such that for each edge $uv$, $f^+(u)$ and $f^+(v)$ are not both even, and $|f^+(u) - f^+(v)| = 2^m, m\ge 0$ is an edge-prime labeling.

Suppose $f$ is an edge labeling of a graph $H=(V,E)$. For each edge $xy$ of $H$, let $d_{xy}=|f^+(x) - f^+(y)|$. We shall use this notation throughout this paper.

1. We say $f$ has Property (A) if $d_{xy}=2^m$ for some $m\ge 0$, and each $xy\in E(H)$.
2. Let $G$ be an edge-prime graph of size $q$. Suppose $H$ is $r$-regular with an edge-prime labeling $f$. We say $f$ has Property (B) if $(d_{xy}, rq)=d_{xy}$, for each $xy\in E(H)$. Moreover, $f$ has Property (C) if for each $xy\in E(H)$, $d_{xy}=2^m$ for some $m\ge 0$ or $(d_{xy}, rq)=d_{xy}$.

Theorem 2. Let $G$ be an edge-prime graph. Suppose $H$ is an $r$-regular graph that admits an edge-prime labeling having Property (A).

1. If $r|E(G)|$ is even or $|E(G+H)|$ is odd, then $G+H$ is edge-prime.
2. If $r|E(G)|$ is odd and $|E(H)|$ is even, then $G+H$ is edge-prime.

Proof. Let $f_1$ and $f_2$ be edge-prime labelings of $G$ and $H$ respectively with $f_2$ satisfying the given condition.

(a). Suppose $r|E(G)|$ is even. Define $g$ such that $g(e) = f_1(e)$ for $e\in E(G)$, and $g(e) = f_2(e) + |E(G)|$ for $e\in E(H)$. Consider an edge $uv\in E(G+H)$. It suffices to consider $uv\in E(H)$. Without loss of generality, assume $f^+_2(u)$ is odd. Now, $g^+(u)=r|E(G)|+f_2^+(u)$ is odd. $$(g^+(u),g^+(v)) = (r|E(G)|+ f^+_1(u), r|E(G)|+ f^+_2(v)) = (g^+(u), f^+_2(u)- f^+_2(v)) = (g^+(u), 2^m) = 1.$$ Suppose $|E(G+H)|=q$ is odd. Define $g$ such that $g(e) = f_1(e)$ for $e\in E(G)$, and $g(e) = q+1- f_2(e)$ for $e\in E(H)$. Again, we only need to consider $uv\in E(H)$. Without loss of generality, assume $f^+_2(u)$ is odd. Now, $g^+(u)=r(q+1)-f_2^+(u)$ is odd. We have $$(g^+(u),g^+(v)) = (rq - f^+_2(u)+r, rq - f^+_2(v)+r) = (g^+(u), f^+_2(u)- f^+_2(v)) = (g^+(u), 2^m) = 1.$$ $$(g^+(u),g^+(v)) = (rq - f^+_2(u)+r, rq - f^+_2(v)+r) = (g^+(u), f^+_2(u)- f^+_2(v)) = (g^+(u), 2^m) = 1.$$ Hence, $g$ is also an edge-prime labeling.

(b). Suppose $r|E(G)|$ is odd and $|E(H)|$ is even. Clearly, $|E(G)|$ is odd, and thus $|E(G+H)|$ is odd. From (a), we get that $G+H$ is also edge-prime.

Theorem 3. Suppose $G$ is a graph of even size $q$ such that every component of $G$ is regular. If $G$ admits an edge-prime labeling $f$ having Property (A), then $nG$ is edge-prime for $n\ge 2$.

Proof. For $k\ge 1$, define a partial edge labeling $g_k$ for the $k$-th copy of $G$ such that $g_k(e)=f(e) + (k-1)q$. Clearly, every induced vertex label in $G$ and the corresponding vertex in the $k$-th copy of $nG$ have the same parity. Moreover, every 2 induced adjacent vertex labels differ by $2^m, m\ge 0$. Hence, $nG$ is edge-prime.

Theorem 4. Suppose every component of $G$ is an even regular graph. If $G$ admits an edge-prime labeling $f$ having Property (A), then $nG$ is edge-prime for $n\ge 2$.

Proof. Let $H$ be a component of $G$, which is $r$-regular. By Theorem 2 (a), since $r$ is even, $G+H$ is edge-prime. We may repeat this procedure for each component of $G$ to show that $2G$ is edge-prime and so is $nG$.

Lemma 5. Suppose $G$ is a graph of size $q$ with an edge-prime labeling $f$. If $H$ is an $r$-regular graph with an edge-prime labeling $g$ having Property (B), then $G+H$ is edge-prime.

Proof. We define an edge labeling $h$ for $G+H$ by $$h(e)=\begin{cases}f(e),&\mbox{ if }e\in E(G);\\ g(e)+q,&\mbox{ if }e\in E(H).\end{cases}$$ We only need to consider edge $uv\in E(H)$. Now, $h^+(u) = g^+(u) + rq$ and $h^+(v) = g^+(v) + rq$. Since $(d_{uv},g^+(v))=(g^+(u), g^+(v))=1$ and $rq$ is a multiple of $d_{uv}$, we have $(h^+(u), h^+(v)) = (g^+(u) + rq, g^+(v) + rq) = (d_{uv},g^+(v) + rq) = 1$. Hence $h$ is an edge-prime labeling and $G+H$ is edge-prime.

When $rq$ is even, or $rq$ is odd and $|E(H)|$ is even, we may relax the condition of Lemma 5 to have the following corollary.

Corollary 6. Suppose $G$ is a graph of size $q$ with an edge-prime labeling $f$, and $H$ is an $r$-regular graph with an edge-prime labeling $g$.

1. Suppose $rq$ is even. If $g$ has Property (C), then $G+H$ is edge-prime.
2. Suppose $rq$ is odd and $|E(H)|$ is even. If $g$ has Property (C), then $G+H$ is edge-prime.

Proof.

(a). We define an edge labeling $h$ for $G+H$ as in Lemma 5. By the proof of Lemma 5, we only need to consider the case when $d_{uv}=2^m$ with $m\ge 0$, where $uv\in E(H)$. Without loss of generality, we may assume $g^+(v)$ is odd. This implies that $h^+(v)$ is odd. By the same computation in the proof of Lemma 5, we have $(h^+(u), h^+(v)) =(d_{uv}, h^+(v))=1$. Hence $G+H$ is edge-prime.

(b). Suppose $rq$ is odd and $|E(H)|$ is even. Clearly, $q$ is odd and $|E(G+H)|$ is odd. Similar to (a), we only need to consider the case when $d_{uv} = 2^m$ with $m\ge 0$, where $uv\in E(H)$. By Theorem 2 (b), we have $G+H$ is edge-prime.

Theorem 7. Suppose $G$ is an $r$-regular graph of size $q$ with an edge-prime labeling $f$. If $f$ has Property (B), then $nG$ is edge-prime.

Proof. The theorem follows by applying Lemma 5 repeatedly.

Corollary 8. Suppose $G$ is an $r$-regular graph of size $q$ with an edge-prime labeling $f$, where $rq$ is even. If $f$ has Property (C), then $nG$ is edge-prime.

Proof. This follows by applying Corollary 6 repeatedly.

Remark 1. Suppose $G$ is an edge-prime graph of size $q$, where $q\equiv 0\pmod{6}$. Suppose $H$ is a cubic graph with an edge-prime labeling $g$. If $d_{xy}\in\{1,2,3,4,6,8\}$ for all $xy\in E(H)$, then $g$ has Property (C).

Remark 2. Note that the induced vertex labeling of each new edge labeling defined at each theorem or corollary above is difference preserved, i.e., all $d_{xy}$ remain unchanged.

We next show the possible existence of non-edge-prime regular graphs.

Theorem 9.

Let $G$ be a $(p,q)$-graph containing $t$ component(s) such that every component of $G$ is of size $e_j$ with $e_j \equiv 1 \pmod{4}$, $1\le j \le t$. Let $f: E(G)\to [1,q]$ be any bijection. Suppose no $2$ adjacent vertex labels of $G$ under $f^+$ are even implies that every component of $G$ receives odd number of odd edge labels under $f$. If $t \equiv 2$ or $3 \pmod{4}$, then $G$ is not edge-prime.

Proof. Let $f$ be any bijective edge labeling of $G$. Suppose $t\equiv 2\pmod{4}$. Now $q \equiv 2 \pmod{4}$. Hence, there are odd number of odd edge labels. There is a component receives even number of odd edge labels under $f$. By the hypothesis, there is a component containing two adjacent vertices whose labels are even. Hence $f$ is not an edge prime labeling. That is, $G$ does not admit an edge-prime labeling.

Similarly, if $t\equiv 3\pmod{4}$, then $q \equiv 3 \pmod{4}$. Hence, there are even number of odd edge labels. There is a component receives even number of odd edge labels under $f$. Hence, $G$ does not admit an edge prime labeling.

2. Cubic graphs with same order components

Lemma 10. If $h$ is an edge labeling of $G=(V,E)$, then there are even number of odd vertex labels.

Proof. The lemma follows from $$\begin{equation}\label{eq-sum} \sum\limits_{u\in V} h^+(v)=2\sum\limits_{e\in E} h(e). \end{equation}$$

Corollary 11. Suppose $f$ is an edge labeling of a graph $G$ such that no adjacent vertex labels are even.

1. Suppose $G$ contains a component $H =K_n$ for $n\ge 3$. If $n$ is even, then all vertex labels in $H$ are odd. If $n$ is odd, then there is exactly one even vertex label in $H$.
2. If $G$ contains a component $K\cong K(m,n)$ with odd $m$ and $n$, then $K$ contains odd number of odd edge labels.

Proof.

(1). By the assumption, $H$ admits at most one even vertex label. By Lemma 10, there is no even vertex label in $H$ if $n$ is even.

(2). Let $(X,Y)$ be the bipartition of a component $K$. If $K$ has even vertex labels, then the corresponding vertices lie in $X$, say. By Lemma 10, there are even number of even vertex labels. Each even vertex label incident with even number of odd edge label as well as each odd vertex label incident with odd number of odd edge label. So, $K$ contains odd number of odd edge labels.

Theorem 12. The graph $nK_4$ is edge-prime if and only if $n \ge 2$.

Proof. (Necessity)

We prove by contrapositive. Suppose there is an edge-prime labeling $f$ of $K_4$. By Corollary 11, all 4 vertex labels are odd and distinct. Since each vertex label lies between $6$ and $15$. So the set of vertex labels is a subset of $\{7,9,11,13,15\}$ of size 4. Since the vertex labels are pairwise relatively prime and the sum of all 4 vertex labels is 42 (from (1)), there is no solution. Hence, $K_4$ is not edge-prime.

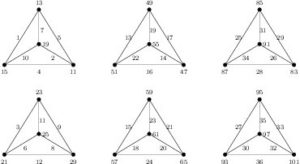
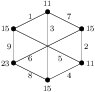
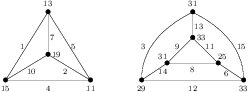
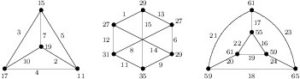
(Sufficiency) (a). Suppose $n=2t$ with $t\ge 1$. The labeling of the two left-most graphs in Figure $\ref{fig:6k4}$ shows that $G=2K_4$ is edge-prime with $d_{xy}\in\{2,4,6,8\}$.

By Remark 1 and Corollary 8, we conclude that $(2t)K_4$ is edge-prime for all $t\ge 1$.
(b). Suppose $n=2t+1$ with $t\ge 1$. If $t=1$, then the labeling in Figure 1 shows that $H=3K_4$ is edge-prime and $d_{xy}\in\{2,4,6,8\}$.

If $t\ge 2$, then we have just known that $G=(2t-2)K_4$ is edge-prime. By Remark 1 and Corollary 6, $G+H=(2t+1)K_4$ is edge-prime.
We now consider cubic graphs with every component of order 6. Each component must be a $C_3\times K_2$ or a $K(3,3)$.

Theorem 13. For $n \ge 1$, $n(C_3 \times K_2)$ is edge-prime.

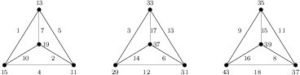
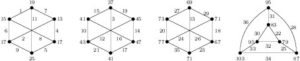
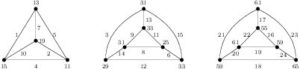
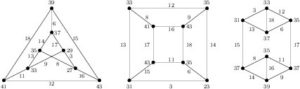
Proof. In Figure 3, the labeling of the two top-left graphs shows that $H=C_3\times K_2$ and $K=2(C_3\times K_2)$ are edge-prime with $d_{xy}\in\{2,4,6,8\}$.

For $n=2t\ge 2$, by Remark 1 and Corollary 8, we have $(2t)(C_3 \times K_2)$ is edge-prime for all $t\ge 1$. Suppose $n=2t+1\ge 1$. Since $H$ is edge-prime, we only need to consider $2t+1\ge 3$. Since we have already known that $G=(2t)(C_3\times K_2)$ is edge-prime, by Remark 1 and Corollary 6 $G+H=(2t+1)(C_3\times K_2)$ is edge-prime.

The next theorem shows that there are infinitely many non-edge-prime cubic graphs.

Theorem 14. For $n \ge 1$, $n(K(3,3))$ is edge-prime if and only if $n \equiv 0$ or $1 \pmod{4}$.

Proof. (Necessity) Suppose $h$ is a bijective edge labeling of $n(K(3,3))$ such that no $2$ adjacent vertex labels are even. By Corollary 11 each component $K(3,3)$ contains odd number of odd edge labels. So, $n(K(3,3))$ satisfies the hypotheses of Theorem 9. Hence if $n(K(3,3))$ is edge-prime, then $n\equiv 0$ or $1\pmod{4}$.
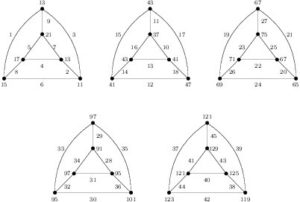
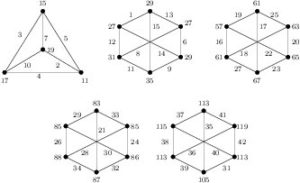
(Sufficiency) (a). Consider $n=4t$. The labeling in Figure 4 shows that $G=4K(3,3)$ is edge-prime with $d_{xy}\in\{1,2,3,4,6,8\}$. Clearly, $G$ satisfies the hypotheses of Corollary 8. Hence, we have $(4t)K(3,3)$ is edge-prime for each $t\ge 1$.

(b). Consider $n=4t+ 1$, $t\ge 0$. The labeling of the graph in Figure 5 shows that $H=K(3,3)$ is edge-prime with $d_{xy}\in\{4,8\}$.

We assume that $t\ge 1$. Since $G=(4t)K(3,3)$ is edge-prime, by Remark 1 and Corollary 6 we have $G+H=(4t+1)K(3,3)$ is edge-prime.

Theorem 15. For $m,n\ge 1$, $m(C_3\times K_2)+nK(3,3)$ is edge prime.

Proof. Case 1. $n=4t$, $t\ge 1$. From Theorem 14 we know that $(4t)K(3,3)$ is edge-prime (with $d_{xy}\in\{1,2,3,4,6,8\}$). From Theorem 13 we know that $m(C_3\times K_2)$ admits an edge-prime labeling with $d_{xy}\in\{2,4,6,8\}$. Since the size of $(4t)K(3,3)$ is $36t$, by Remark 1 and Corollary 6 we have $(4t)K(3,3)+m(C_3\times K_2)$ is edge-prime with $d_{xy}\in\{1,2,3,4,6,8\}$.
Case 2. $n=4t+1$, $t\ge 0$. Combining the labeling of $K(3,3)$ in Figure 5 and the labeling of $C_3\times K_2$ in the top-middle of Figure 3 we have an edge-prime labeling of $(C_3\times K_2)+K(3,3)$ (with $d_{xy}\in\{2,4,6,8\}$). From Theorem 13, Theorem 14 or Case 1, $(m-1)(C_3\times K_2)+(4t)K(3,3)$ admits an edge-prime labeling $g$ with $d_{xy}\in\{1,2,3,4,6,8\}$, $m\ge 1$ and $t\ge 0$. Since the size of $C_3\times K_2$ is 18, $g$ has Property (C). By Corollary 6 we obtain that $[(C_3\times K_2)+K(3,3)]+[(m-1)(C_3\times K_2)+(4t)K(3,3)]=m(C_3\times K_2)+(4t+1)K(3,3)$ is edge-prime.

Case 3. $n=4t+2$, $t\ge 0$. From Case 2 or Theorem 14, there is an edge-prime labeling of $(m-1)(C_3\times K_2)+(4t+1)K(3,3)$ with $d_{xy}\in\{1,2,3,4,6,8\}$ for $m\ge 1$ and $t\ge 0$. By the same argument as in Case 2, we have $[(C_3\times K_2)+K(3,3)]+[(m-1)(C_3\times K_2)+(4t+1)K(3,3)]=m(C_3\times K_2)+(4t+2)K(3,3)$ is edge-prime.
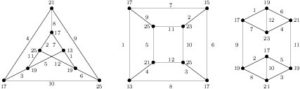
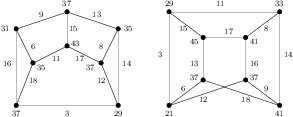
Case 4. $n=4t+3$, $t\ge 0$. Consider the edge-prime labeling of $(C_3\times K_2)+3K(3,3)$ as shown in Figure 6.

From Theorem 13, Theorem 14, or Case 1, $(m-1)(C_3\times K_2)+(4t)K(3,3)$ admits an edge-prime labeling $g$ with $d_{xy}\in\{1,2,3,4,6,8\}$, $m\ge 1$ and $t\ge 0$. Since the size of $(C_3\times K_2)+3K(3,3)$ is 36, by Corollary 6 we get that $m(C_3\times K_2)+(4t+3)K(3,3)$ are edge-prime. Note that the resulting labeling induces $d_{xy}\in\{1,2,3,4,6,8,12,16\}$.
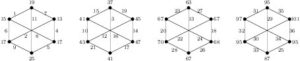
It is known that there are exactly 5 connected cubic graphs of order 8. Figure 7 shows edge-prime labelings of these 5 graphs, denoted $G_k$, $1\le k\le 5$.

Theorem 16. If every component of $G$ is a connected cubic graph of order 8, then $G$ is edge-prime.

Proof. Since each edge labeling shown in the Figure 7 induces $d_{xy}\in\{2,4,6,8\}$. By Remark 1 and applying Corollary 6 repeatedly, the theorem holds.

3. Cubic graphs with distinct order components

In this section, we completely determine the edge-primality of cubic graphs with components of distinct orders of 4, 6 or 8.

Theorem 17. For $m,n \ge 1$, $mK_4 + n(C_3\times K_2)$ is edge-prime.

Proof. Suppose $m\ge 2$. From Table 1 we know that $mK_4$ and $n(C_3\times K_2)$ are edge-prime when $m\ge 2$ and $n\ge 1$. Since $|E(mK_4)|=6m$ and $d_{xy}\in\{2,4,6,8\}$ under the edge-prime labeling of $n(C_3\times K_2)$, by Remark 1 and Corollary 6, $mK_4 + n(C_3\times K_2)$ is edge-prime.
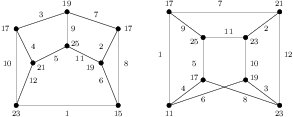
Suppose $m=1$. Consider odd $n$. The edge-prime labeling of $K_4+(C_3\times K_2)$ shown in Figure 8 with $d_{xy}\in\{2,4,6,8\}$. For $n\ge 3$, from Table 1 we know that $(n-1)(C_3\times K_2)$ is edge-prime with size $9(n-1)$. By Corollary 6, $(n-1)(C_3\times K_2) + [K_4+(C_3\times K_2)]=K_4+n(C_3\times K_2)$ is edge-prime with $d_{xy}\in\{2,4,6,8\}$.

Consider even $n$. Figure9 shows that $K_4 + 2(C_3\times K_2)$ is edge-prime. Using Table 1 and by Corollary 6, if needed, we get that $[K_4 + 2(C_3\times K_2)] + (n-2)(C_3\times K_2) = K_4 + n(C_3\times K_2)$ is edge-prime with $d_{xy}\in\{2,4,6,8\}$.

Theorem 18. For $m, n \ge 1$, the graph $m K_4 + n K(3,3)$ is edge-prime.

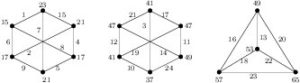
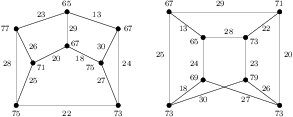
Proof. (a). Suppose $n\equiv 0,1\pmod{4}$. Suppose $m$ is even. By Table 1, we know that $mK_4$ and $nK(3,3)$ are edge-prime. Note that $d_{xy}\in\{1,2,3,4,6,8\}$ for $xy\in E(nK(3,3))$ and $|E(mK_4)|=6m$. By Remark 1 and Corollary 6, we get the result.
Suppose $m$ is odd. From the whole figure and the two top-left graphs of Figure $\ref{fig:K44K(33)}$ we see that $K_4+K(3,3)$ and $K_4+4K(3,3)$ are edge-prime with $d_{xy}\in\{1,2,3,4,6,8\}$.

By Table 1 or the above case, there is an edge-prime labeling of $(m-1)K_4+4(t-1)K(3,3)$ for odd $m\ge 1$ and $t\ge 1$. Since $|E((m-1)K_4+4(t-1)K(3,3))|=6(m-1)+36(t-1)$, the labelings of $K_4+K(3,3)$ and $K_4+4K(3,3)$ have Property (C). By Corollary 6 we get that $mK_4+(4(t-1)+1)K(3,3)$ and $mK_4+(4t)K(3,3)$ are edge-prime. Note that $d_{xy}\in\{1,2,3,4,6,8\}$ for the resulting edge labelings above.
(b). Suppose $n\equiv 2,3\pmod{4}$. Figure $\ref{fig:2K(33)K4}$ shows that $K_4+2K(3,3)$ is edge-prime.

From the above case, there is an edge-prime labeling $g$ of $(m-1)K_4+(n-2)K(3,3)$ with $d_{xy}\in \{1,2,3,4,6,8\}$ for $m\ge 1$ and $n\ge 2$. Since $|E(K_4+2K(3,3))|=24$, $g$ has Property (C). By Corollary 6 we have $mK_4+nK(3,3)$ is edge-prime.

The following Table 1 gives a summary of the edge-prime labelings obtained above together with the set of the difference of adjacent vertex labels $d_{xy}$.

Table 1. Results from Theorems 12 to 18.

Graph $G$	Condition(s)	$\{d_{xy}\;|\; xy\in E(G)\}$
$nK_4$	$n\ge 2$	$\{2,4,6,8\}$
$n(C_3\times K_3)$	$n\ge 1$	$\{2,4,6,8\}$
$nK(3,3)$	$n\equiv 0,1\pmod{4}$	$\{1,2,3,4,6,8\}$
$m(C_3\times K_2)+nK(3,3)$	$m,n\ge 1$	$\{1,2,3,4,6,8,12,16\}$
$mK_4 + n(C_3\times K_2)$	$m,n\ge 1$	$\{2,4,6,8\}$
$mK_4 + nK(3,3)$	$m,n\ge 1$	$\{1,2,3,4,6,8,12,16\}$
$\sum_{i=1}^5 n_iG_i$	$\sum_{i=1}^5 n_i\ge 1$	$\{2,4,6,8\}$

Theorem 19. For $m_1, m_2, m_3\ge 1$, the graph $m_1K_4 + m_2K(3,3)+m_3(C_3\times K_2)$ is edge-prime.

Proof. (a). Suppose $m_2$ is even. From Table 1, $m_1K_4+m_2(K(3,3))$ is edge-prime and $m_3(C_3\times K_2)$ admits an edge-prime labeling with $d_{xy}\in\{2,4,6,8\}$. Since the size of $m_1K_4+m_2K(3,3)$ is $6(m_1+3m_2/2)$, by Corollary 6, we have the theorem.
(b). Suppose $m_2$ is odd. For even $m_3$, from the case (a) or Table 1, $m_1K_4+(m_2-1)K(3,3)+m_3(C_3\times K_2)$ is edge-prime with even size. From Figure 5 there is an edge-prime labeling of $K(3,3)$ with $d_{xy}\in\{4,8\}$. By Corollary 6 we have the theorem.
Now, assume that $m_3$ is odd. If $m_1=m_2=m_3=1$, then Figure 12 shows an edge-prime labeling of $K_4+K(3,3)+(C_3\times K_2)$.

So we assume that at least one of $m_1,m_2, m_3$ is greater than 1. From Case (a) or Table 1, $m_1K_4+(m_2-1)K(3,3)+(m_3-1)(C_3\times K_2)$ is edge-prime with the size a multiple of 6. From the proof of Theorem 15 there is an edge-prime labeling of $(C_3\times K_2)+K(3,3)$ with $d_{xy}\in\{2,4,6,8\}$. By Corollary 6 we have the theorem.

Remark 3 The set of $d_{xy}$ of the edge-prime labeling obtained above is $\{1,2,3,4,6,8,12,16\}$.

Theorem 20. The graph $mK_4 + \sum^5_{i=1} n_iG_i$ is edge-prime for all $m \ge 1$ and $\sum^5_{i=1} n_i \ge1$.

Proof. Suppose $m \ge 2$. From Table 1 and by Corollary 6 we get the theorem. Suppose $m = 1$. For $1 \le k \le 5$, we choose the smallest $k$ such that $n_k > 0$ and label $K_4 + G_k$ from 1 to 18. The $K_4$ is labeled by $1,2,4,5,7,10$ as shown in Figure 9. The labeling of each $G_k$ by $\{3,6,8,9\}\cup[11,18]$, if needed, is labeled by the remaining labels shown in Figure 13.

The remaining unlabeled subgraph, if any, admits an edge-prime labeling with $d_{xy}\in\{2,4,6,8\}$ by Table 1. By Corollary 6 we obtain the theorem.

Theorem 21. The graph $m(C_3\times K_2) +\sum^5_{i=1} n_iG_i$ is edge-prime for $m \ge 1$ and $\sum^5_{i=1} n_i \ge1$.

Proof. From Table 1 we know that there are edge-prime labelings of $\sum^5_{k=1} n_iG_i$ and $m(C_3\times K_2)$ with $d_{xy}\in\{2,4,6,8\}$. Since the size of $\sum^5_{k=1} n_iG_i$ is 12 multiple, by Corollary 6 we have the theorem.

Theorem 22. The graph $mK(3,3)+\sum^5_{i=1} n_iG_i$ is edge-prime for $m \ge 1$ and $\sum^5_{i=1} n_i \ge1$.

Proof. (a). Suppose $m\equiv 0,1\pmod{4}$. From Table 1 we know that there are edge-prime labelings of $\sum^5_{i=1} n_iG_i$ and $mK(3,3)$ with $d_{xy}\in\{1,2,3,4,6,8\}$. Since the size of $\sum^5_{i=1} n_iG_i$ is a 12 multiple, by Corollary 6 we have the theorem. Note that the set of difference adjacent vertex labels of the new edge-prime labeling is $d_{xy}\in\{1,2,3,4,6,8\}$.
Suppose $m\equiv 2,3\pmod{4}$. For $1 \le k \le 5$, we choose the smallest $k$ such that $n_k > 0$ and label $2K(3,3) + G_k$ from 1 to 30. Figure 4 shows an edge labeling of $2K(3,3)$ labeled by integers in $[1,21]\setminus\{13, 18,20\}$ with $d_{xy}\in\{2,4,6,8\}$. The labeling of each $G_k$ by $\{13,18,20\}\cup [22,30]$, if needed, is shown in Figure 14.

From Case (a) or Table 1 there is an edge-prime labeling of $(m-2)K(3,3)+\sum\limits_{\begin{smallmatrix}1\le i\le 5\\i\ne k\end{smallmatrix}} n_iG_i$, if any, with $d_{xy}\in\{1,2,3,4,6,8\}$. Since the size of $2K(3,3) + G_k$ is 30, by Corollary 6 we have the theorem.

Theorem 23. For $m_1, m_2\ge 1$ and $\sum^5_{i=1}n_i\ge 1$, the graph $m_1K_4 + m_2(C_3\times K_2) + \sum^5_{i=1} n_iG_i$ is edge-prime.

Proof. The size of $\sum^5_{i=1}n_iG_i$ is a multiple of 12. From Table 1 and by Corollary 6 we have the theorem.

Theorem 24. For $m_1, m_2\ge 1$ and $\sum^5_{i=1}n_i\ge 1$, the graph $m_1K_4 + m_2K(3,3) + \sum^5_{i=1} n_iG_i$ is edge-prime.

Proof. The size of $\sum^5_{i=1}n_iG_i$ is a multiple of 12. From Table 1 and by Corollary 6 we have the theorem.

Theorem 25. \label{v6v8} For $m_1, m_2\ge 1$ and $\sum^5_{i=1}n_i\ge 1$, the graph $m_1(C_3\times K_2)+$ $m_2K(3,3) +$ $\sum^5_{i=1} n_iG_i$ is edge-prime.

Proof. The size of $\sum^5_{i=1}n_iG_i$ is a multiple of 12. From Table 1 and by Corollary 6 we have the theorem.

Theorem 26. Let $m_1, m_2, m_3, \sum^5_{i=1} n_i\ge 1$, the graph $m_1 K_4 + m_2 (C_3\times K_2) + m_3 K(3,3) +$ $\sum^5_{i=1}G_i$ is edge-prime.

Proof. The size of $\sum^5_{i=1}n_iG_i$ is a multiple of 12. From Remark 3 and by Corollary 6 we have the theorem.

Corollary 27. If $G$ is a cubic graph with every component of order 4, 6 or 8, then $G$ is edge-prime if and only if $G\not\cong K_4$ or $nK(3,3)$, $n\equiv2,3\pmod{4}$.

In [7], we proved that (i) a 1-regular graph is edge-prime if and only if it is $K_2$, (ii) all 2-regular graphs are edge-prime, and (iii) if $G$ is edge-prime, then $G+ C_n$ $(n\ge 3)$ and $G+ K(1,2)$ are edge-prime.

Corollary 28. Let $G$ be an edge-prime graph as in Sections 2 and 3. For $\sum m_k\ge 1, n_k\ge 3$, $G+ \sum m_k C_{n_k}$ and $G+ K(1,2)$ are edge-prime.

4. Open problems

Problem 29. Determine the edge-primality of the following families of cubic graphs.

1. cylinder graph $C_n\times K_2$, $n\ge 5$.
2. Möbius ladder $M(2n)$, $n\ge 2$.
3. generalized Petersen graph $P(n,k)$, $n\ge 5, k\ge 2$.

It is easy to verify that $K_n$ is edge-prime for $n=2,3,5,6,7$ but not $n=4$, and $K(n,n)$ is edge-prime for $n=2,3,4$. We end with the following conjecture.

Conjecture 4.1. For $n\ge 2$, we have

1. $K_n$ is edge-prime if and only if $n\not= 4$.
2. $K(n,n)$ is edge-prime.
3. All connected cubic graphs, except $K_4$, are edge-prime.

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest:

The authors declare no conflict of interest.