Open Journal of Discrete Applied Mathematics
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2020.0029
Capacitated vehicle routing problem with column generation and reinforcement learning techniques
Department of Mathematical Sciences, Baze University Abuja, Nigeria.; (A.I)
Department of Mathematical Sciences, African Institute for Mathematical Sciences, Mbour, Senegal.; (J.I)
SATWII solutions Inc. Canada.;(N.L)
Department of Energy Engineering, Pan African University of Water and Energy Resources, University of Tlemcen, Algeria.; (R.A)
\(^{1}\)Corresponding Author: abdullahi.ibrahim@bazeuniversity.edu.ng; Tel.: +2348067497949
Abstract
Keywords:
1. Introduction
The concept of Vehicle Routing Problem (VRP) was first proposed in [1] and a mathematical programming formulation and algorithm method for VRP were also developed in this study. This problem generalizes the famous and common Traveling Salesman Problem (TSP) which is one of the simplest routing problems. According to [2], the TSP involves finding the optimal/shortest route that connects all routes exactly once and return to the starting node from a given set of finite route and also measuring the distance between them. Due to the set of several available routes, VRP is a computationally difficult problem even though many algorithms (such as heuristic and exact algorithm) have been proposed over the years. The challenging task is how to produce a solution that will be fast and reliable.
The VRP is a combinatorial optimization and integer programming problem which finds optimal path in order to deliver goods and services to a finite set of customers. It can be described as a graph \(G(\mathcal{V}, \mathcal{E})\) where \(\mathcal{V}\) denote the set of nodes and \(\mathcal{E}\) denote the weighted edges between the nodes. The VRP has been a problem for several decades and one of the most studied problem in logistics engineering, applied mathematics and computer science, and which is described as finding optimal routes for a fleet of vehicles to serve some scattered customers from depot [1, 3, 4, 5, 6].
The Capacitated VRP (CVRP) involves finding set of optimal routes for some fleets of homogeneous vehicles with capacity constraints, moving from a central depot to service customer demands and return to same depot. Our basic assumption before solving CVRP includes; for the customer, the quantity of demand and the traveling cost from one customer to another are known, and for the vehicles, the exact number of vehicles and its capacity must be known.
The VRP consists of several variants which includes; TSP [7, 8, 9, 10], Multiple TSP [11, 12], CVRP [10, 13, 14], VRP with time windows (VRPTW) [15, 16], dynamic VRP (DVRP)[17, 18], pickup and delivery VRP (PDVRP)[19], periodic VRP (PVRP)[20] and so on. These variants have several application which include; DVRP is applicable in the courier services [21], Milk-collection problem [22], and so on.
In this paper, our goal is to find optimal set of routes for some vehicles delivering goods or services to some known locations. Further, the capacity of these homogeneous vehicles must not be exceeded. To achieve this goal, we shall;
- formulate a mathematical model for the CVRP problem,
- develop a reinforcement learning framework for solving CVRP, and
- check the optimal gap between column generation, Google's operations research tools and reinforcement learning.
Our proposed algorithm is different from [5] and will be applied on Augerat et al.,[14] instances. The remainder of our paper is broken down as follows: Section 2 shows the literature review. Section 3 introduces the mathematical model of CVRP and algorithms to be used. The various techniques discussed are then applied on CVRP in Section 4. A summary of the findings and proposed future research directions are finally given in Section 5.
2. Literature review
Some researchers came up with significant ideas which has really contributed to solving VRP and transportation problem in general. In the first article [1], some trial problems were calculated but no practical application was made. Based on the first article [1], Clarke and Wright in [27] developed a saving-based heuristics algorithm that enables rapid selection of optimal or near-optimal route. Augerat et al., [14] applied three algorithm namely; constructive, randomized greedy and a very simple tabu search algorithms to separate capacity constraints from CVRP and some experimental results (from known instances and romdomly generated instances) with these algorithms were reported. Toth and Vigo [28] reviewed exact algorithms based on branch-and-bound approach and applied it on CVRP. Experimental results comparing the performance of different relaxations and algorithms on some instances were also presented. Fukasawa et al., [29] applied branch-and-cut-and-price algorithm to solve several instances of CVRP to optimality. Baldacci and Mingozzi [30] solved a CVRP problem using an exact method based on set-partitioning formulation of the problem. The proposed method was effective but has limited solving power of customers to about 100. Uchoa et al., [31] proposed and used new set of CVRP instances ranging from \(100\) to \(1000\) customers. Some exact and heuristic methods were also applied on the proposed instances.
Akhtar et al., [32] applied Backtracking Search Algorithm (BSA) on CVRP in order to minimize travel cost for waste collection routes distances. The obtained results showed \(36.80%\) distance reduction and reducing the fuel cost by \(4.77%\), thus the BSA algorithm was concluded to be a viable tool. Franco et al., [33] used Nearest Neighbor Algorithm (NNA) to perform a comparative study between Augerat et al., [14] instances to solve CVRP and determine which instance offers the best solution. In their work, there was \(15.7%\) improvement on \(opt-A-n33-k5\) instance. Rojas-Cuevas et al., [34] used Capacitated Vehicle Routing Problem for Carriers (CVRPfC) to solve distribution problem. The route planning were obtained through CVRPfC and the authors concluded that the CVRPfC can improve the competitiveness of the carriers by providing better fares to their customers. Ibrahim with his coauthors [7, 13] applied column generation to solve CVRP to optimality using Augerat et al., [14] instances. Kohl et al., [35] and Desrochers et al.,[1]author11} applied column generation to solve VRP with time windows. Some experimental results were presented and it was concluded that the algorithm are helpful in solving VRP with practical-sized VRPTW benchmark.
Reinforcement learning, pointer network and Neural combinatorial Optimization have also been applied in solving VRP. Bello et al., [25] proposed a neural networks and reinforcement learning to solve VRP with single vehicle. The algorithm (Neural combinatorial Optimization) achieved near-optimal results on \(2D\) euclidean graphs upto \(100\) nodes. Ishaya et al., [8] improved the algorithms given in [25], by adding 2-opt search on the algorithms to achieve a near-optimal solution and was able to solve upto 200 nodes. Nazari et al., [5] presented a reinforcement learning framework for solving the VRP. The model was applied on VRP and TSP and this approach perform very well on medium-sized problem in terms of the solution quality with computational time. Advantage of this method is that it scales well when the problem-size is increasing.
3. Mathematical Model and Methodology
3.1. Nomenclature definitions
All vehicles will originate and end at the depot, while each of the customer is visited exactly once. Let us define the following:- \(\mathcal{C} = \{1, 2,\dots, m\}\) represent the set of m-customers to be considered,
- \(\mathcal{V} = \{{v_{0}},{v_{1}}, \dots, {v_{m}},{v_{m+1}}\}\) is the set of vertices in G. The vertices \(v_{0}= v_{m+1}\) represent the depot, and \(\{{v_{1}},\dots,{v_{m}}\}\) represent customers nodes,
- \(\mathcal{E} = \{({v_{i}}, {v_{j}}) \hspace{.2cm} \vert \hspace{.2cm} 0 \le i,j \le m, \hspace{.2cm}i\ne j \}\) is a set of \(\vert \mathcal{V} \vert \ast (\vert \mathcal{V} \vert - 1)\) directed routes/edges between the vertices. If in both directions the distance between two vertices are identical, we then add the \((i < j)\) restriction,
- K denote the fleet of available vehicles in a single depot. All vehicles considered are homogeneous \emph{i.e.,} equal capacities. We have \(n\)-vehicles,
- Q is the maximum capacity of a vehicle, which limits the number of customers to be visited before returning to the depot,
- \(\pi(a \vert s)\) is the probability density function,
- \(\mathcal{A}\) is the set of actions,
- \(Q(s,a;\pi)\) is the action value function,
- \(\vert x_1 - x_2 \vert + \vert y_1 - y_2 \vert\) is the manhattan distance,
- \(\pi\) is the policy,
- \(P(s,a,y)\) is the transitive probability,
- \(a_n\) is the alignment vector,
- C \(= (c_{ij})\) is the cost of traveling from nodes \(i\) to \(j\) and \(c_{ij}\ge 0\) is the corresponding distance of edges \((v_{i},v_{j})\), the diagonal of the matrix i.e \(c_{ii} = 0\) always. Depending on whether the VRP variant in consideration is symmetric or not, \(c_{ij} = c_{ji}\). The triangle inequality is assumed to hold generally, \emph{i.e.,} \(c_{ij} \le c_{ik}+c_{kj}\) and \((0 \le i,j,k \le m)\),
- \(R_i = (v_{0}^{i}, v_{1}^{i},v_{2}^{i}, v_{3}^{i} \dots, v_{k_i}^{i}, v_{k_{i+1}}^{i})\) is a vector of the route of vehicle \(i\) which start and end at the depot, with \(v_{0}^{i} = v_{k_{i+1}}^{i} = v_{0}, v_{j}^{i} \ne v_{\ell}^{i}, 0 \le j < \ell \le k_i\), and \(k_i\) is the length of route \(R_i\),
- \(\mathcal{S} = \{R_1,\dots, R_n\}\) is the set of route which represent the VRP solution instance,
- C\((R_{i}) = \sum_{j=0}^{k_i}\) C\((v_{j}^{i}, v_{j+1}^{i})\) is the cost of route \(R_i\),
- C\(\mathcal{(S)} = \sum_{i=1}^{n}\) C\((R_i)\) is the total cost of solution \(\mathcal{S}\) which satisfies \(R_i \cap R_j = \{v_0\}\hspace{.3cm} \forall R_i, R_j, (1\le i,j \le n, i\ne j)\) and \(\cup_{i=1}^{n}R_i = \mathcal{S}\) in order for each customer to be served once. The route vectors is treated here as a set.
- demand; \(d = (d_0, \dots, d_m, d_{m+1})\) with \(d_i> 0\) and \(m\) is the total number of customers which is a vector of the demands of customer, the demand of the depot is denoted by \(d_0\); \(d_0 = d_{m+1} = 0\) always.
- Let us define our decision variable; \(x_{ijk} = \left\{ \begin{array}{rcl} 1 & \mbox{iff vehicle \(k\) moves from node \(i\) to \(j\)} \\ \\ 0 & \mbox{otherwise.} \end{array}\right.\)
- q\(_{j}\) is the quantity of demand at node \(j\)
- The capacity constraints of all the vehicles are observed.
- Each customer can be served by only one vehicle.
- Each and every route starts at vertex \(0\) and ends at vertex \((m+1)\).
Note that subtours are avoided in the solution with constraint (5) that is, cycling paths which do not pass through the depot. Constraints (5) and (6) advantage in this problem is that in terms of our customers, the formulation has a polynomial number of constraints.
However, the Linear Programming (LP) relaxation of this formulation (model) generate a lower bound which is known to be weak when compared to other models. Many researchers and authors emphasized on capacity constraints that produce a better lower bounds, although the constraints increases exponentially in terms of number of customer thereby requiring the application of branch and cut (BAC) technique[36].
3.2. Column generation (CG) technique
In order to solve our objective function (1), we shall apply CG technique. This technique is efficient in solving large linear program problems [37]. The idea of this technique is that LP problems are usually too large and difficult to consider all variables explicitly. CG considers variables with potential to improve our objective function and this strategy helps to reduce the number of variables. In CG, the problem is splitted into some iterative steps which are; Restricted Master Problem and Pricing Problem.3.3. Restricted master problem (RMP)
We are going to use set-partitioning to re-write the objective function. Let us recall that in problem definition Section 3.1 we defined We shall introduce following variables here: \begin{align*} y_{k} = \left\{ \begin{array}{rcl} 1 & \mbox{if route k is in the solution} \\ \\ 0 & \mbox{otherwise.} \end{array}\right. \end{align*} and \begin{align*} a_{ik} = \left\{ \begin{array}{rcl} 1 & \mbox{if customer i use route k} \\ \\ 0 & \mbox{otherwise.} \end{array}\right. \end{align*} Also, we denote \(C_k\) as the total costs of driving a route, this include cost of overtime, fixed cost, early and late arrival penalties. Then, we formulate the objective function as:3.4. The pricing-problem (subproblem)
In order to solve the CVRP with column generation approach, the pricing-algorithm decomposes into \(\vert \mathcal{V} \vert\) identical problems, where each of the problem is a shortest path problem with time windows and capacity constraints. Specifically, the pricing-problem is an elementary shortest path with capacity and time windows constraints (ESPWCTWC), the elementary shortest path implies that each customer cannot appear more than once in the shortest path. We can now formulate the subproblem as follow,Solving the subproblem as a linear mixed integer programming will potentially reduce the integrality gap between optimal integer solution and the relaxed version of the CVRP problem, since the subproblem does not have integrality constraint/property[37]. More literatures on column generation technique can be obtain in[29, 38, 39, 40, 41, 42, 43, 44, 45]. The column generation algorithm is given in Algorithm 2.
3.5. Google's operations research tool
The second technique to be used is the Operations Research Tools (Goole's OR-Tool). Goole's OR-Tool is an open source software suitable for solving optimization problems. The algorithm is suitable in solving routing problem, constraint programming, flows problem, integer programing and so on[46]. The advantage of this software to us is that it enables us to find optimal tour and its length for routing problem using python. Its computational time is usually very fast compared to other techniques. Its solutions are usually near-optimal when compared with exact method. The algorithm computes distance between two points; \((x_{1}, y_{1})\), \((x_{2}, y_{2})\), using the manhattan distance which sum up the absolute distance of \(x\) and \(y\) coordiantes respectively. This can be obtained mathematically as \( \vert x_1 - x_{2} \vert + \vert y_1 - y_2 \vert \). We convert the algorithm's formula for computing the cost of transportation by computing the distance between two coordinates; \((x_{1}, y_{1})\), \((x_{2}, y_{2})\), i.e., using the Euclidean formula \(\sqrt{(x_{1} - x_{2})^2 + (y_{1} - y_{2})^2} \). One major advantage is that the algorithm is computationally very fast. Application of this technique shall be given in Section 4.3.6. Reinforcement learning
Reinforcement learning (RL) is the learning of what-to-do, how to map situations to actions in order to maximize a numerical reward signal. The learner (agent) is not explicitly told the actions to take, but instead discover which actions yield more rewards by trying different action. RL provides a mathematical framework suited to solving games. In RL, Markov Decision Process (MDP), tool for modeling artificial intelligence agents that interacts with environment that offers rewards on completion of some certain actions, is the central mathematical concept[47].Markov decision processes (MDP)
MDP is defined as a stochastic process in discrete time. The mathematical space of MDP has a defined states \(S\), for each state a reward signal \(r: S \times \mathcal{A} \rightarrow \mathcal{R}\). The agent has some actions, \(\mathcal{A}\), and probability distribution \(P(y\vert s,a)\), with current state \(s \in S\) and action \(a \in \mathcal{A}\), the probability of moving into given state \(y\). In this environment, the goal is to find a policy, \(\pi : S \rightarrow \mathcal{A}\) in order to maximize the discounted sum of total rewards \(R\) over all time steps3.7. Sequence-to-sequence model
Sequence-to-sequence models[23, 24, 49] are handy in tasks for which mapping from one sequence to another is required[5]. Over the past several years, these models have been studied extensively in the field of neural machine translation, and there are many variants of these models. Generally speaking, the architecture for the different versions is almost the same, which consists of two Recurrent Neural Networks (RNN), called the encoder and decoder. An encoder network reads through the input sequence and store the output knowledge in a fixed size sequence of vectors, and a decoder converts the encoded information back to an input sequence.3.8. Neural combinatorial optimization
Several methods have been developed in order to solve a combinatorial optimization problem using recent techniques in artificial intelligence. Vinyals et al.,[24] was the first who first proposed the concept of Pointer Network, model inspired by sequence-to-sequence models [5]. Because it is invariant to the encoder sequence length, the Pointer Network enables the model to be applicable to combinatorial optimization problems, where the length of output sequence is determined by the source sequence. Vinyals et al., [24] used the pointer network architecture in supervised fashion in order to find a near optimal tours for TSPs from heuristic solutions. This dependence limits the Pointer Network from obtaining better solutions order than the ones provided during the training.3.9. The model
In this section, we introduce our model, which is the simplified version of the Pointer Network. We formally define the problem and our proposed framework for generic combinatorial optimization problem with a set of input \(X = {x^{j}, j \dot{=} 1,2,\dots, N}\). Some elements of each input is allowed to change between the decoding steps, which is the case in several combinatorial problems such as the VRP. The dynamic elements might be an artifact of the decoding step itself, or they can be imposed by the environment. We represent every input \(x^{j}\) by a sequence of tuples \(\{x_{n}^{j} \dot{=} (s^{j}, d_{n}^{j}), n = 0,1,2,\dots\}\), where \(s^{j}\) and \(d_{t}^{j}\) are the static and dynamic elements of input, respectively, which can also be a tuples. \(x_{n}^{j}\) can be viewed as a vector which describes at time n the state of input \(j\). We will represent the set of all input states at fixed time \(n\) with \(X_{n}\). Starting with an arbitrary input in \(X_{0}\) and pointer \(z_{0}\) refer to this input. At every decoding time \(n, z_{n+1}\) points to one of the available \(X_{n}\), which will determine the input for the next decoding step; and this process goes on and on until a termination condition is satisfied. The termination condition is specific on a particular problem, showing that the sequence generated satisfies the feasibilty constraints. For instance, for the CVRP considered in this work, the terminating condition is satisfied when there is no more demand to be satisfied.
This process will generate sequence of length \(N, Z = \{z_{n}, n=0,1,\dots,N\}\), with a different sequence-length (probably), when compared with the length of the input sequence \(M\). The reason is, the vehicle may have to return to the depot to refill several times. Furthermore, we use \(Z_{n}\) to denote the decoded sequence up to time \(n\). Our interest is to find a stochastic policy \(\pi\) that will generates the sequence \(Z\) in a way that minimizes a loss objective function while the problem constraints are satisfied. The optimal policy \(\pi^{*}\) will generate the optimal solution with probability \(1\). Our goal to to make the optimal gap between \(\pi\) and \(\pi^{*}\) close to zero.
Similar to[23], in order to decompose the probability of generating sequence \(Z\) we use the probability chain rule, as follows:3.10. Attention mechanism
Attention mechanism is a differentiable structure for addressing different parts of the input. The attention mechanism employed in our method is illustrated in[5]. In words, \(a_{n}\) specifies how much every input data point might be relevant in the next decoding step n. Set the embedded input \(j\) as \(\bar{x}_{n}^{j} = (\bar{s}^{j}, \bar{d}_{n}^{j})\), and \(f_{n} \in \mathbb{R}^{D}\) is the memory state of the RNN cell at decoding step n. The alignment vector \(a_n\) is computed as;For training the policy gradient, we utilize the REINFORCE approach (in algorithm 0) which can be found in[5,8, 25] for VRP. Consider \(\mathcal{N}\) problems with probability distribution \(\Phi_{\mathcal{N}}\).
4. Results
We show the applications of Column Generation, Google's OR-Tools and Reinforcement Learning on Capacitated Vehicle Routing Problem. Our results were compared with best known values for each instances. These techniques have been previously discussed explicitly in Section 3, and Augerat et al., [14] instances will be use to test these methodologies and their results shall be compared. For our experiments, we used HP Elitebook \(840\) PC, \(1.9\)GHz processor, core i\(5\) with \(8\)GB Memory. We started by showing optimal tour with tables and graphs for Column generation, Google's OR-Tools and comapre them with reinforcement learning. We used Augerat et al., [14] (set P) data to perform our experiment. The optimality gap here is computed as4.1. Column generation applied on CVRP
The Column Generation (CG) method is an exact method for solving the CVRP and the VRP in general, this technique has been explicitly explained in Section 3.2, and gives an optimal solution to a small-size problem but become inefficient on big-size problem.
Table 3 gives the summary of the comparison of this technique's primal and dual problem, since CG work on dual solution of the relaxed master problem, their optimal gap in percentage. The table 3 consists of seven columns; Instances (contains the instances written as \(P-n16-k8\) which means the data consists of \(16\) nodes with \(8\) fleets of vehicles),Cities (locations to be visited), Best value (from literature), Relaxed Master Problem (RMP), Column Generation (based on dual values), column generation computational time and optimality gap. From the table, the optimal gap for all the instances considered gives \(0.00%\). From the instances we consider in this research, only coordinates and demands for each nodes are given, CG compute the distance between two coordinates; \((x_{1}, y_{1})\), \((x_{2}, y_{2})\), using the euclidean formula;Table 1. CG results.
| Instances | Cities | Best value | RMP (primal) | CG result (cost) | CG time | gap |
|---|---|---|---|---|---|---|
| P-n16-k8 | 16 | 450 [50] | 450 | 450.00 | 14.72 | 0.00% |
| P-n20-k2 | 20 | 220 [50] | 220 | 220.00 | 38.64 | 0.00% |
| P-n22-k2 | 22 | 216 [50] | 216 | 216.00 | 44.31 | 0.00% |
| P-n22-k8 | 22 | 603 [50] | 603 | 603.00 | 19.66 | 0.00% |
| P-n40-k5 | 39 | 458 [50] | 458 | 458.00 | 32.22 | 0.00% |
| P-n50-k10 | 49 | 696 [50] | 696 | 696.00 | 38.42 | 0.00% |
| P-n101-k4 | 100 | 681 [50] | 681 | 681.00 | 39.16 | 0.00% |
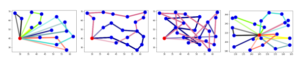
Figure 1. Optimal routes for some instances in table 3.
4.2. Google's OR-tool applied on CVRP
We applied Google's OR-Tool on CVRP as follow, the optimal gap formula is given in (31)Table 2. Goole's OR-Tool results.
| Instances | Best known values | Google’s OR-Tool | Optimality gap | |
|---|---|---|---|---|
| result | time (s) | |||
| A-n32-k5 | 784*[50] |
796 |
.04 | 1.53% |
| P-n16-k8 | 450*[50] | 450 | .50 | 0.00% |
| P-n20-k2 | 216*[50] | 227 | .02 | 5.09% |
| P-n22-k2 | 216*[50] | 217 | .02 | 0.46% |
| P-n22-k8 | 603*[50] | 623 | .51 | 3.32% |
| P-n40-k5 | 458*[50] | 494 | .10 | 7.86% |
| P-n50-k7 | 554*[50] | 574 | .08 | 3.61% |
| P-n70-k10 | 827*[50] | 940 | .17 | 13.66% |
| P-n101-k4 | 681*[50] | 741 | .35 | 8.81% |
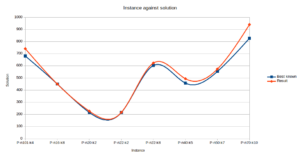
Figure 2. Plot showing optimal gap between Google’s OR-Tool and Best known solution
Similarly, the tour for instance \(p-n101-k4\) with cost \(741\) is given as follow:
\( R_1 = (v_{28}, v_{12}, v_{68}, v_{80}, v_{54}, v_{24}, v_{29}, v_{3}, v_{77}, v_{79}, v_{78}, v_{34}, v_{35}, v_{65}, v_{66}, v_{71}, v_{9}, v_{81}, v_{33}, v_{51}, v_{20}, v_{30}, v_{70}, v_{31}, v_{88}, v_{7}, v_{52} )\),
\( R_2 = ( v_{89}, v_{60}, v_{5}, v_{84}, v_{17}, v_{45}, v_{47}, v_{36}, v_{49}, v_{64}, v_{63}, v_{90}, v_{32}, v_{10}, v_{62}, v_{11}, v_{19}, v_{48}, v_{82}, v_{8}, v_{32}, v_{18} ) \),
\( R_3 = (v_{27}, v_{69}, v_{1}, v_{50}, v_{76}, v_{26}, v_{58}, v_{13}, v_{94}, v_{95}, v_{97}, v_{87}, v_{57}, v_{15}, v_{43}, v_{100}, v_{85}, v_{93}, v_{59}, v_{99}, v_{96}, v_{6} ) \),
\(R_4 = ( v_{92}, v_{37}, v_{98}, v_{91}, v_{61}, v_{16}, v_{86}, v_{44}, v_{38}, v_{14}, v_{42}, v_{2}, v_{41}, v_{22}, v_{23}, v_{67}, v_{67}, v_{39}, v_{25}, v_{55}, v_{4}, v_{56}, v_{75}, v_{74}, v_{72}, v_{73}, v_{21},\\ \;\;\;\;\;v_{40}, v_{53} )\,. \)
4.3. CG, Google's OR-tools and RL on CVRP
So far we have shown the results for each of our methodologies i.e CG in Table 3, Google's OR-Tool with our algorithm in Table 1. Now, we compute the final table which summarize the CG, Google's OR-Tool and RL techniques and shown in Table 1. We use Beam Search with width \(10\) (BS10) for the RL.Table 3. Summary of CG, Google's OR-Tools and RL results.
| Instance | best value | CG | Google’s OR-Tool | RL | |||
|---|---|---|---|---|---|---|---|
| result (gap) | time(s) | result (gap) | time(s) | result (gap) | time(s) | ||
| P-n16-k8 | 450*[50] | 450 (0.00%) | 14.72 | 450 (0.00%) | 0.50 | 451 (0.22%) | 0.30 |
| P-n20-k2 | 216*[50] | 216 (0.00%) | 38.64 | 227 (5.09%) | .20 | 220 (1.85%) | 0.45 |
| P-n22-k2 | 216*[50] | 216 (0.00%) | 44.31 | 217 (0.46%) | .20 | 218 (0.93%) | 0.55 |
| P-n22-k8 | 603*[50] | 603 (0.00%) | 19.66 | 623 (3.32%) | .51 | 615 (2.67%) | 1.10 |
From our comparison Table 1 above, we see that the first technique; column generation solution gives us the best bound, of course we expect nothing less since the technique gives an optimal solution but limited to a small size problem. The second technique, the Google's OR-Tool solution gives a near-optimal solution and the advantage of this technique over the previous is, it solves more problems than CG. The optimal gap for each of the instances considered using this technique is \(< 15%\). Lastly, the reinforcement learning also gives a new optimal solution compared with the previous two techniques. Its solutions outperform the OR-tools and is closer to the exact solution, the optimality gap is quite smaller compared with the Google's OR-Tool optimality gap. This technique is quite good since it can handle a large-size problem.
The computational time for each of these techniques are also of importance, since we want an algorithm that will be fast in computations. Although the CG technique gives an optimal solution, it has high computational time when compared with OR-Tools and RL. The Google's OR-Tool and RL appear to have 'almost' the same computational time and lesser than CG time, which shows these two techniques perform their experiment faster than the CG. The Optimal gap between the CG and OR-Tools is \(0.00%\) on instance \(P-n16-k8\). The gap between the CG and RL appears to be better and smaller ib value when compared with the gap between CG and OR-Tools.
4.4. Google's OR-Tools and RL with CVRP
Google's OR-Tools and RL have been compared with CG previously on small-sized problem. Here, we shall compare these two techniques to solve bigger-size problems. Table 4 shows the path-length and computational time for these techiques and their optimal gap. The ``instances" column shows the size of the problems and their vehicle capacity, Q. From Table 4, both technique's result are shown with their computational times. Our RL outperforms the google's OR-Tools. The solutions here are scaled down to \([0,1] \times [0,1]\) for a better solution. We have shown results using various techniques discussed and their tour-length cost, optimal tour, optimality gap and computational time. Each of these technique is applied on the same data set and the same PC was used to perform these experiments.Table 4. OR-Tools and RL result.
| Instances | OR-Tools | RL | optimality gap | ||
|---|---|---|---|---|---|
| path-length | time | path-length | time | ||
| vrp50, Q=150 | 31.50 | 0.29 | 30.88 | 02.25 | 2.01% |
| vrp70, Q=135 | 36.05 | 0.29 | 35.74 | 03.02 | 0.87% |
| vrp100, Q=400 | 55.62 | 0.29 | 55.05 | 06.23 | 1.04% |
5. Conclusion
The three algorithms discussed here; column generation, google's OR-Tools and reinforcement learning algorithms are examined on a small-scale problem. Also, google's OR-Tools and reinforcement learning are examined on large scale data. An algorithm that will find a near-optimal solution have been developed. We find the optimal set of routes for a fleet of vehicles delivering goods or services to various locations. In order to achieve this aim, we formulated a mathematical formulation for the Capacitated Vehicle Routing Problem. We further to solved this formulation with the three techniques; Column generation, Google's Operational Research tool and Reinforcement Learning. We compared the objective values for these techniques with the ''best known values" and calculated for the ``optimality gap'' between this solution, taking the ''best known value" as the lower bound. From our experiment, our Reinforcement Learning outperformed the google's OR-Tools a little bit. Although the computational time for the google's OR-Tools is faster than the Reinforcement Learning time but these experimental times are very close and the reinforcement learning is able to solve a large data set.
In our future work, a ``time window" constraint can be added to this problem. Basically, this problem shall have multiple vehicles with capacity constraint and each location will have a time window. This means that each of the customer/location will require demand at a particular time window \([a_i , b_i ]\), where \(a_i\) is the opening time at a location and a vehicle must arrive on or before \(a_i\) and \(b_i\) is the closing time, a vehicle is not allowed to come after \(b_i\) . Hence, the delivery time, \(s_i\) to a location must be \(a_i \le s_i \le b_i\) . Customers with similar time window can be merged together as long as the capacity limit of the vehicle is not exceeded.
Acknowledgments
We appreciate African Institute for Mathematical Science, Senegal for full funding in order to carry out this research at AIMS.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Conflicts of Interest:
The authors declare no conflict of interest.References
- Dantzig, G. B., & Ramser, J. H. (1959). The truck dispatching problem. Management science, 6(1), 80-91.[Google Scholor]
- Ropke, S. (2005). Heuristic and exact algorithms for vehicle routing problems.\\ https://backend.orbit.dtu.dk/ws/portalfiles/portal/3155278/Heuristic+and+exact+algorithms+for+vehicle+routing +problems\_Ropke.pdf[Google Scholor]
- Fukasawa, R., Longo, H., Lysgaard, J., De Aragão, M. P., Reis, M., Uchoa, E., & Werneck, R. F. (2006). Robust branch-and-cut-and-price for the capacitated vehicle routing problem. Mathematical programming, 106(3), 491-511.[Google Scholor]
- Golden, B. L., Raghavan, S., & Wasil, E. A. (Eds.). (2008). The vehicle routing problem: latest advances and new challenges (Vol. 43). Springer Science & Business Media.[Google Scholor]
- Nazari, M., Oroojlooy, A., Snyder, L., & Takác, M. (2018). Reinforcement learning for solving the vehicle routing problem. In Advances in Neural Information Processing Systems (pp. 9839-9849). [Google Scholor]
- Kallehauge, B., Larsen, J., Madsen, O. B., & Solomon, M. M. (2006). Recent advances in the vehicle routing problem with time windows. In Odysseus 2006.[Google Scholor]
- Ibrahim, A. A., Abdulaziz, R. O., Ishaya, J. A., & Samuel, O. S. (2019). Vehicle Routing Problem with Exact Methods. IOSR Journal of Mathematics, 15(3), 05-15.[Google Scholor]
- Ishaya, J., Ibrahim, A., & Lo, N. (2019) A comparative analysis of the travelling salesman problem: Exact and machine learning techniques. Open Journal of Discrete Applied mathematics, 2(3), 23-37[Google Scholor]
- Clingerman, C., Hemphill, J., & Proscia, C. (2008). Analysis and Counterexamples Regarding Yatsenko's Polynomial-Time Algorithm for Solving the Traveling Salesman Problem. arXiv preprint arXiv:0801.0474.[Google Scholor]
- Ibrahim, A., Ishaya, J., Abdulaziz, R., & Samuel, S., (2020) Solving some variants of vehicle routing problem with Branch-and-cut and Column generation algorithms. Open Journal of Mathematical Sciences, 4, 63-73.[Google Scholor]
- Bektas, T. (2006). The multiple traveling salesman problem: an overview of formulations and solution procedures. Omega, 34(3), 209-219. [Google Scholor]
- Tang, L., Liu, J., Rong, A., & Yang, Z. (2000). A multiple traveling salesman problem model for hot rolling scheduling in Shanghai Baoshan Iron & Steel Complex. European Journal of Operational Research, 124(2), 267-282.[Google Scholor]
- Ibrahim, A. A., Lo, N., Abdulaziz, R. O., & Ishaya, J. A. (2019). Capacitated Vehicle Routing Problem. International Journal of Research-Granthaalayah, 7(3), 310-327.[Google Scholor]
- Augerat, P., Belenguer, J. M., Benavent, E., Corbéran, A., & Naddef, D. (1998). Separating capacity constraints in the CVRP using tabu search. European Journal of Operational Research, 106(2-3), 546-557.[Google Scholor]
- Kohl, N., Desrosiers, J., Madsen, O. B., Solomon, M. M., & Soumis, F. (1999). 2-path cuts for the vehicle routing problem with time windows. Transportation Science, 33(1), 101-116.[Google Scholor]
- Dror, M. (1994). Note on the complexity of the shortest path models for column generation in VRPTW. Operations Research, 42(5), 977-978. [Google Scholor]
- De Magalhaes, J. M., & De Sousa, J. P. (2006). Dynamic VRP in pharmaceutical distribution-a case study. Central European Journal of Operations Research, 14(2), 177-192. [Google Scholor]
- Kilby, P., Prosser, P., & Shaw, P. (1998). Dynamic VRPs: A study of scenarios. University of Strathclyde Technical Report, 1-11.[Google Scholor]
- Desaulniers, G., & Groupe d'études et de recherche en analyse des décisions (Montréal, Québec). (2000). The VRP with pickup and delivery. Groupe d'études et de recherche en analyse des décisions. [Google Scholor]
- Rahimi-Vahed, A., Crainic, T. G., Gendreau, M., & Rei, W. (2013). A path relinking algorithm for a multi-depot periodic vehicle routing problem. Journal of Heuristics, 19(3), 497-524.[Google Scholor]
- Gendreau, M., Guertin, F., Potvin, J. Y., & Séguin, R. (2006). Neighborhood search heuristics for a dynamic vehicle dispatching problem with pick-ups and deliveries. Transportation Research Part C: Emerging Technologies, 14(3), 157-174.[Google Scholor]
- Claassen, G. D. H., & Hendriks, T. H. (2007). An application of special ordered sets to a periodic milk collection problem. European Journal of Operational Research, 180(2), 754-769.[Google Scholor]
- Sutskever, I., Vinyals, O., & Le, Q. V. (2014). Sequence to Sequence Learning with Neural Networks. arXiv preprint arXiv:1409.3215.[Google Scholor]
- Vinyals, O., Fortunato, M., & Jaitly, N. (2015). Pointer networks. In Advances in Neural Information Processing Systems, (pp. 2692-2700).[Google Scholor]
- Bello, I., Pham, H., Le, Q. V., Norouzi, M., & Bengio, S. (2016). Neural combinatorial optimization with reinforcement learning. arXiv preprint arXiv:1611.09940.[Google Scholor]
- Curtin, K. M., Voicu, G., Rice, M. T., & Stefanidis, A. (2014). A comparative analysis of traveling salesman solutions from geographic information systems. Transactions in GIS, 18(2), 286-301.[Google Scholor]
- Clarke, G., & Wright, J. W. (1964). Scheduling of vehicles from a central depot to a number of delivery points. Operations research, 12(4), 568-581.[Google Scholor]
- Toth, P., & Vigo, D. (2002). Models, relaxations and exact approaches for the capacitated vehicle routing problem. Discrete Applied Mathematics, 123(1-3), 487-512.[Google Scholor]
- Fukasawa, R., Lysgaard, J., De Aragão, M. P., Reis, M., Uchoa, E., & Werneck, R. F. (2004, June). Robust branch-and-cut-and-price for the capacitated vehicle routing problem. In International Conference on Integer Programming and Combinatorial Optimization (pp. 1-15). Springer, Berlin, Heidelberg.[Google Scholor]
- Baldacci, R., & Mingozzi, A. (2006, October). Lower bounds and an exact method for the Capacitated Vehicle Routing Problem. International Conference on Service Systems and Service Management, (Vol. 2, pp. 1536-1540). IEEE.[Google Scholor]
- Uchoa, E., Pecin, D., Pessoa, A., Poggi, M., Vidal, T., & Subramanian, A. (2017). New benchmark instances for the capacitated vehicle routing problem. European Journal of Operational Research, 257(3), 845-858.[Google Scholor]
- Akhtar, M., Hannan, M. A., Begum, R. A., Basri, H., & Scavino, E. (2017). Backtracking search algorithm in CVRP models for efficient solid waste collection and route optimization. Waste Management, 61, 117-128.[Google Scholor]
- Franco, E. G. C., Aguilar, J. A. H., Ochoa-Zezzatti, A., & Gallegos, J. C. P. (2018). Comparison between instances to solve the CVRP. International Journal of Combinatorial Optimization Problems and Informatics, 9(2), 41-54.[Google Scholor]
- Rojas-Cuevas, I. D., Caballero-Morales, S. O., Martinez-Flores, J. L., & Mendoza-Vazquez, J. R. (2018). Capacitated vehicle routing problem model for carriers. Journal of Transport and Supply Chain Management, 12(1), 1-9.[Google Scholor]
- Desrochers, M., Desrosiers, J., & Solomon, M. (1992). A new optimization algorithm for the vehicle routing problem with time windows. Operations research, 40(2), 342-354.[Google Scholor]
- Semet, F., Toth, P., & Vigo, D. (2014). Chapter 2: Classical exact algorithms for the capacitated vehicle routing problem. In Vehicle Routing: Problems, Methods, and Applications, Second Edition (pp. 37-57). Society for Industrial and Applied Mathematics.[Google Scholor]
- van Lent, G. P. T. (2018). Using column generation for the Time Dependent Vehicle Routing Problem with Soft Time Windows and Stochastic Travel Times (Master's thesis). https://dspace.library.uu.nl/handle/1874/361947.[Google Scholor]
- Pal, S. (2005). Improving Branch-And-Price Algorithms For Solving One Dimensional Cutting Stock Problem. In MTech Seminar Report. Mumbai: Indian Institute of Technology.[Google Scholor]
- Nemhauser, G. L. (2012). Column generation for linear and integer programming. Optimization Stories, 20, 65–73.[Google Scholor]
- Hennig, F., Nygreen, B., & Lübbecke,, M. E. (2012). Nested column generation applied to the crude oil tanker routing and scheduling problem with split pickup and split delivery. Naval Research Logistics (NRL), 59(3-4), 298-310.[Google Scholor]
- Desrosiers, J., & Lübbecke, M. E. (2010). Branch-price-and-cut algorithms. Wiley encyclopedia of operations research and management science.[Google Scholor]
- Lübbecke, M. E. (2005). Dual variable based fathoming in dynamic programs for column generation. European Journal of Operational Research, 162(1), 122-125.[Google Scholor]
- Desrosiers, J., Gauthier, J. B., & L\(\dddot{u}\)bbecke, M. E. (2014). Row-reduced column generation for degenerate master problems. European Journal of Operational Research, 236(2), 453-460.[Google Scholor]
- Villeneuve, D., Desrosiers, J., L\(\dddot{u}\)bbecke, M. E., & Soumis, F. (2005). On compact formulations for integer programs solved by column generation. Annals of Operations Research, 139(1), 375-388.[Google Scholor]
- Desaulniers, G., Desrosiers, J., & Solomon, M. M. (Eds.). (2006). Column generation (Vol. 5). Springer Science & Business Media.[Google Scholor]
- Inc. google. google's optimization tools, 2019, webpage, https://github.com/google/or-tools, 2019.
- Sutton, R. S., & Barto, A. G. (1998). Reinforcement learning: an introduction. MIT Press. Cambridge, MA. [Google Scholor]
- \(\ddot{O}\)dling, D. (2018). A metaheuristic for vehicle routing problems based on reinforcement learning. Master thesis. http://www.diva-portal.org/smash/record.jsf?pid=diva2\%3A1191148\&dswid=-9662 [Google Scholor]
- Luong, M. T., Pham, H., & Manning, C. D. (2015). Effective approaches to attention-based neural machine translation. arXiv preprint arXiv:1508.04025.[Google Scholor]
- Capacitated Vehicle Routing Problem Library (CVRPLIB) http://vrp.galgos.inf.puc-rio.br/index.php/en/ (accessed in January 2020).
- Inc. Gurobi Optimization. gurobi optimizer reference manual, 2019, url, http://www.gurobi.com, (assessed deccember 2019). [Google Scholor]