Open Journal of Discrete Applied Mathematics
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2020.0040
Complex dynamics of a fractional-order predator-prey interaction with harvesting
Rizwan Ahmed
Department of Mathematics, National College of Business Administration and Economics, Rahim Yar Khan, Pakistan.; rizwanahmed488@gmail.com
Abstract
Keywords:
1. Introduction
Fractional differential equations are more suitable for modeling many real-life phenomena than ordinary differential equations. Fractional calculus has seen significant development over the past few decades. Chaos is a very interesting nonlinear phenomenon which has been intensively studied due to its useful applications in science and technology [1,2,3]. Studying chaos in fractional-order dynamical systems is an interesting topic as well. The discrete fractional equations recently attracted researchers in the modeling of the biological populations and interaction of the species [4,5,6,7]. Harvesting has a strong impact on the dynamic evolution of a population subjected to it. The effects of predator harvesting were reported in [8,9], harvesting among two fish species and its effects were studied in [10].
In this paper, the predator-prey model is considered with harvesting effort affecting both species directly. We studied the following fractional-order predator-prey model.
The paper is organized as follows. In Section 2, we investigate the topological classification of the unique positive equilibrium point of the system (2). In Section 3, we discuss period-doubling bifurcation and in Section 4, we discuss Neimark-Sacker bifurcation at positive steady-state. In Section 5, some numerical examples are presented to verify our theoretical results. In Section 6, some concluding remarks are presented.
2. Local stability of positive equilibrium point
The system (2) has three equilibrium points. \[ E_0\left(0,0\right), E_1\left(\frac{a-c}{a},0\right), E_2\left(\frac{d+f}{e},\frac{ae-ad-af-ce}{be}\right). \] Note that if \(ae-ad-af-ce>0\), then \(E_2\) is the unique positive equilibrium point of (2). \(E_0\) is the mutual extinction, \(E_1\) is the predator extinction and \(E_3\) is coexistence equilibrium point of system (2). For bilogically meaningful we concentrated on coexistence equilibrium point \(E_2\). The jacobian matrix of (2) evaluated at \(E_2\) is given by \[ J(E_2)= \begin{bmatrix} 1-\frac{aM(d+f)}{e} & \frac{-bM(d+f)}{e} \\ -\frac{(ce+a(d-e+f))M}{b} & 1 \end{bmatrix}, \] where \(M=\frac{k^{\alpha}}{\Gamma({\alpha+1})}\). The corresponding characteristic polynomial isLemma 1. [13]: Let \(F(\lambda)=\lambda^2-A \lambda+B\), where \(A, B\) are constants. Suppose \(F(1)>0\) and \(\lambda_1, \lambda_2\) are roots of \(F(\lambda)=0\), then
- (i) \(|\lambda_1|< 1\) and \(|\lambda_2|< 1\) iff \(F(-1)>0\) and \(F(0)< 1\).
- (ii) \(|\lambda_1|< 1\) and \(|\lambda_2|>1\) iff \(F(-1)< 0\).
- (iii) \(|\lambda_1|>1\) and \(|\lambda_2|>1\) iff \(F(-1)>0\) and \(F(0)>1\).
- (iv) \(\lambda_1=-1\) and \(|\lambda_2|\neq 1\) iff \(F(-1)=0\) and \(F(0)\neq \pm 1\).
- (v) \(\lambda_1\) and \(\lambda_2\) are complex and \(|\lambda_1|=|\lambda_2|=1\) iff \(A^2-4B< 0\) and \(F(0)=1\).
Theorem 1. If \((a,b,c,d,e,f,M)\in \mathbb{R}_+^7, \ ae-ad-af-ce>0\) and \(\lambda_1, \lambda_2\) are the roots of \(F(\lambda)=0\) given by (3), then
- (i) \(|\lambda_1|< 1\) and \(|\lambda_2|< 1\) iff \[ a-\frac{a(1+dM+fM)}{eM}< c< a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM}, \]
- (ii) \(|\lambda_1|< 1\) and \(|\lambda_2|>1\) iff \[ c>a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM}, \]
- (iii) \(|\lambda_1|>1\) and \(|\lambda_2|>1\) iff \[ c< min \lbrace a-\frac{a(1+dM+fM)}{eM}, a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM} \rbrace, \]
- (iv) \(\lambda_1=-1\) and \(|\lambda_2|\neq 1\) iff \[ c=a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM}, \ c \neq a-\frac{a(1+dM+fM)}{eM}, \ c \neq a+\frac{2}{(d+f)M^2}-\frac{a(1+dM+fM)}{eM}, \]
- (v) \(\lambda_1\) and \(\lambda_2\) are complex and \(|\lambda_1|=|\lambda_2|=1\) iff \[ c=a-\frac{a(1+dM+fM)}{eM}, \ \frac{a(d+f)M}{e}< 4. \] The following corollary is an immediate consequence of Theorem 1.
- (i) a sink and therefore locally asymptotically stable if \[ a-\frac{a(1+dM+fM)}{eM}< c< a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM}, \]
- (ii) saddle point and therefore unstable if \[ c>a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM}, \]
- (iii) source or repeller and therefore unstable if \[ c< min \left\lbrace a-\frac{a(1+dM+fM)}{eM}, a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM} \right\rbrace, \] and
- (iv) non-hyperbolic if \[ c=a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM}, \ c \neq a-\frac{a(1+dM+fM)}{eM}, \ c \neq a+\frac{2}{(d+f)M^2}-\frac{a(1+dM+fM)}{eM}, \] or \[ c=a-\frac{a(1+dM+fM)}{eM}, \ \frac{a(d+f)M}{e}< 4. \]
Corollary 1. If \((a,b,c,d,e,f,M)\in \mathbb{R}_+^7, \ ae-ad-af-ce>0\), then the unique positive equilibrium point \(E_2\) of (2) is:
3. Period doubling bifurcation
In this section, we investigate that system (2) undergoes period doubling bifurcation [14,15] at the positive equilibrium point \(E_2\). Consider \begin{eqnarray*} \Lambda&=&\left\lbrace (a,b,c,d,e,f,M) \in \mathbb{R}^7_+\right. \Big| ae-ad-af-ce>0,\;\; c=a+\frac{4}{(d+f)M^2}-\frac{a(2+dM+fM)}{eM}, \\&& c \neq a-\frac{a(1+dM+fM)}{eM},\;\; c \neq a+\frac{2}{(d+f)M^2}\left.-\frac{a(1+dM+fM)}{eM} \right\rbrace. \end{eqnarray*} We discuss the period doubling bifurcation of the system (2) at \(E_2\) when parameters vary in a small neighborhood of \(\Lambda\). Taking \(c\) as bifurcation parameter, we consider a perturbation of the system (2) as follows:We define a transformation by \(\xi(t)=x(t)-\frac{d+f}{e}\) and \(\eta(t)=y(t)-\frac{a(e-d-f)-(c+\delta)e}{be}\) to transfer the equilibrium point \(E_2\) to \((0,0)\). Under this transformation system (4) will become
Theorem 2. If \((a,b,c,d,e,f,M)\in \Lambda\) and \(L \neq 0, M \neq 0\) then the system (2) goes under period doubling bifurcation at the equilibrium point \(E_2\). Moreover, if \(M>0\) (or \(M< 0\)) then period-2 orbits that bifurcate from the equilibrium point \(E_2\) are stable (or unstable).
4. Neimark-Sacker bifurcation
In this section, we investigate that system (2) undergoes Neimark-Sacker bifurcation [19,20] at the positive equilibrium point \(E_2\). Consider \[ \Omega=\left\lbrace (a,b,c,d,e,f,M) \in \mathbb{R}^7_+ \mid ae-ad-af-ce>0, \ c=a-\frac{a(1+dM+fM)}{eM}, \ \frac{a(d+f)M}{e}< 4 \right\rbrace, \] where \(M=\frac{k^{\alpha}}{\Gamma(\alpha+1)}\).We discuss the Neimark-Sacker bifurcation of the system (2) at \(E_2\) when parameters vary in a small neighbourhood of \(\Omega\). Taking \(c\) as bifurcation parameter, we consider a perturbation of the system (2) as follows:
We define a transformation by \(\xi(t)=x(t)-\frac{d+f}{e}\) and \(\eta(t)=y(t)-\frac{a(e-d-f)-(c+\delta)e}{be}\) to transfer the equilibrium point \(E_2\) to \((0,0)\). Under this transformation system (10) will become
The characteristic equation of the linearized part of the system (11) at equilibrium point \((0,0)\) is
The roots of (12) are complex with \(|\lambda_{1,2}|=1\) which are given by \( \lambda_{1,2}=\frac{p(\delta)\pm i \sqrt{4q(\delta)-p^2(\delta)}}{2}. \) By computations, we obtain \( |\lambda_1|=|\lambda_2|=\sqrt{q(\delta)}, \) and \( \left(\frac{d|\lambda_1|}{d \delta}\right)_{\delta=0}=\left(\frac{d|\lambda_2|}{d \delta}\right)_{\delta=0}=-\frac{(d+f)M^2}{2}< 0. \)
By simple computations, we can check that \(p(0)=2-\frac{a(d+f)M}{e}\). Since \(\frac{a(d+f)M}{e}< 4\), therefore we have \(-2< p(0)< 2\). If we set \(p(0)=0\), then we obtain \(\frac{a(d+f)M}{e}=2\) and if we set \(p(0)=1\), then we obtain \(\frac{a(d+f)M}{e}=1\). Since \(\lambda_1^m,\lambda_2^m \neq1\) for \(m=1,2,3,4\) at \(\delta=0\) is equivalent to \(p(0) \neq \pm 2, 0,1\), therefore \(\lambda_1^m,\lambda_2^m \neq1\) for \(m=1,2,3,4\) at \(\delta=0\) if \((a,b,c,d,e,f,M)\in \Omega\) and following conditions are satisfied:
Theorem 3. Assume that \((a,b,c,d,e,f,M)\in \Omega\) and conditions (13) are satisfied. If \(L \neq 0\), then the system (2) goes under Neimark-Sacker bifurcation at the unique positive equilibrium point \(E_2\) when the parameter \(c\) varies in a small neighbourhood of \(c=a-\frac{a(1+dM+fM)}{eM}\). Furthermore, if \(L< 0\), then an attracting invariant closed curve bifurcates from the equilibrium point for \(c>a-\frac{a(1+dM+fM)}{eM}\), and if \(L>0\), then a repelling invariant closed curve bifurcates from the equilibrium point for \(c< a-\frac{a(1+dM+fM)}{eM}\).
5. Numerical examples
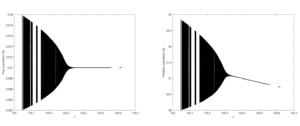
In this section some interesting numerical examples are provided to validate our theoretical discussions on various qualitative aspects of the model.Example 1. We select the parameters values as \(a=200, b=0.8, d=2.3, e=40,f=0.5, k=0.15,\alpha=0.95\) and initial conditions \(x(0)=0.1, y(0)=8\). For these values the unique positive equilibrium point of (2) is \((0.07,11.2316)\). The eigenvalues of \(J(E_2)\) for these values are \(\lambda_1=-1, \lambda_2=0.643641\), which confirms that the system (2) undergoes period doubling bifurcation at \((0.07,11.2316)\) as bifurcation parameter passes through \(c=177.015\). We plot bifurcation diagrams for both prey and predator populations for \(c \in [176,180]\). (see Figure 1)
Figure 1. Bifurcation diagrams for prey and predator populations with \(a=200, b=0.8, d=2.3, e=40,f=0.5, k=0.15,\alpha=0.95, x(0)=0.1, y(0)=8, c \in [176,180].\)
Example 2. We select the parameters values as \(a=200, b=0.8, d=2.3, e=40,f=0.5, k=0.15,\alpha=0.95\) and initial conditions \(x(0)=0.1, y(0)=35\). For these values the unique positive equilibrium point of (2) is \((0.07,37.1336)\). The eigenvalues of \(J(E_2)\) for these values are \(\lambda_1=-0.17818+0.983998i, \lambda_2=-0.17818-0.983998i\) with \(|\lambda_{1,2}|=1\), which confirms that the system (2) undergoes Neimark-Sacker bifurcation at \((0.07,37.1336)\) as bifurcation parameter passes through \(c=156.293\). We plot bifurcation diagrams for both prey and predator populations for \(c \in [156,156.7]\). (see Figure 2 )
Figure 2. Bifurcation diagrams for prey and predator populations with \(a=200, b=0.8, d=2.3, e=40,f=0.5, k=0.15,\alpha=0.95,x(0)=0.1, y(0)=35,c \in [156,156.7].\)
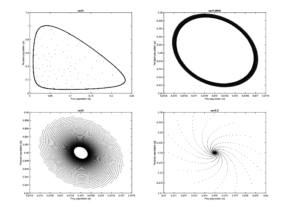
Example 3. We select the parameters values as \(a=20, b=10, d=2, e=40, f=1, k=0.11, \alpha=0.9\) and the initial conditions \(x(0)=0.073, y(0)=0.35\). The positive equilibrium point for these values is \((0.075,0.35058)\). For these values the equilibrium point is locally asymptotically stable iff \(14.9942< c< 77.0381\). We plot phase portraits for \(c=14, 14.9942, 15, 15.2 \). Clearly one can see that for \(c=14\), the equilibrium point \((0.35058,0.142621)\) is unstable, whereas for \(c=15\) and \(c=15.2\) it is stable. For \(c=14.9942\), the system undergoes bifurcation. (See figure 3 )
Figure 3. Phase portraits for prey and predator populations with \(a=20, b=10, d=2, e=40,f=1, k=0.11,\alpha=0.9,x(0)=0.05, y(0)=0.3\) for \(c=14, 14.9942, 15, 15.2\)
6. Conclusion
We studied a fractional-order predator-prey model with harvesting in both species. We study the existence and local stability of coexistence equilibrium point \(E_2\) of system (2) and their dependence in the form of constant harvesting effort of prey. Moreover, the system (2) goes under period-doubling bifurcation and Neimark-Sacker bifurcation under certain conditions on constant harvesting effort of prey. Numerical examples are presented to support our theoretical results.conflictofinterests
The author declares no conflict of interest.References
- He, Z., & Lai, X. (2011). Bifurcation and chaotic behavior of a discrete-time predator-prey system. Nonlinear analysis real world applications, 12(1), 403-417. [Google Scholor]
- Singh, H., Dhar, J., & Bhatti, H. S. (2015). Discrete-time bifurcation behavior of a prey-predator system with generalized predator. Advances in Difference Equations, 2015(1), 206. [Google Scholor]
- Din, Q. (2018). Stability, bifurcation analysis and chaos control for a predator-prey system. Journal of Vibration and Control, 25(3), 612-626.[Google Scholor]
- Elsadany, A. A., & Matouk, A. E. (2015). Dynamical behaviors of fractional-order Lotka Volterra predator-prey model and its discretization. Applied Mathematics and Computation, 49, 269-283. [Google Scholor]
- Nosrati, K., Shafiee, M. (2017). Dynamic analysis of fractional-order singular Holling type-II predator-prey system. Applied Mathematics and Computation, 313, 159-179. [Google Scholor]
- Wang, Z., Xie, Y., Lu, J., & Li, Y. (2019). Stability and bifurcation of a delayed generalized fractional-order prey-predator model with interspecific competition. Applied Mathematics and Computation, 347, 360-369. [Google Scholor]
- Alidousti, J., & Ghafari, E. (2020). Dynamic behavior of a fractional order prey-predator model with group defense. Chaos, Solitons & Fractals, 134, 109688. [Google Scholor]
- Myerscough, M. R., Gray, B. F., Hogarth, W. L., & Norbury, J. (1992). An analysis of an ordinary differential equation model for a two-species predator-prey system with harvesting and stocking. Journal of Mathematical Biology, 30, 389-411. [Google Scholor]
- Hu, D., Cao, H. (2017). Stability and bifurcation analysis in a predator-prey system with Michaelis-Menten type predator harvesting. Nonlinear Analysis Real World Applications, 33, 58-82.[Google Scholor]
- Kar, T. K., & Chaudhuri, K. S. (2003). On non-selective harvesting of two competing fish species in the presence of toxicity. Ecological Modelling, 161(1), 125-137.[Google Scholor]
- Agarwal, R. P., El-Sayed, A. M., & Salman, S. M. (2013). Fractional-order Chua’s system: discretization, bifurcation and chaos. Advances in Difference Equations, 2013(1), 1-13.[Google Scholor]
- Zhang, J., Nan, J., Du, W., Chu, Y., & Luo, H. (2016). Dynamic analysis for a fractional-order autonomous chaotic system. Discrete Dynamics in Nature and Society, 2016, 8712496. [Google Scholor]
- Liu, X. L., & Xiao D. M. (2007). Complex dynamic behaviors of a discrete-time predator-prey system. Chaos, Solitons & Fractals, 32(1), 80-94. [Google Scholor]
- Agiza, H. N., Elabbasy, E. M., EL-Metwally, H., & Elsadany, A. A. (2009). Chaotic dynamics of a discrete prey-predator model with Holling type II. Nonlinear Analysis Real World Applications, 10(1), 116-129. [Google Scholor]
- Jana, D. (2013). Chaotic dynamics of a discrete predator-prey system with prey refuge. Applied Mathematics and Computation, 224, 848-865. [Google Scholor]
- Guckenheimer, J., & Holmes, P. J. (1983). Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York. [Google Scholor]
- Wiggins, S. (2003). Introduction to Applied Nonlinear Dynamical Systems and Chaos. Springer, New York. [Google Scholor]
- Kuznetsov, Y. (2004). Elements of Applied Bifurcation Theory. Springer, New York. [Google Scholor]
- Zhu, L., & Zhao, M. (2009). Dynamic complexity of a host-parasitoid ecological model with the Hassell growth function for the host. Chaos, Solitons & Fractals, 39(3), 1259-1269. [Google Scholor]
- Din, Q., Gumus, O. A., & Khalil, H. (2017). Neimark-Sacker bifurcation and chaotic behaviour of a modified host-parasitoid model. Zeitschrift fur Naturforschung A, 72(1), 25-37. [Google Scholor]