On odd prime labeling of graphs

1. Introduction

We follow [1,2] and [3] for the definitions and notations in graph theory and number theory respectively. We denote to the greatest common divisor of two positive integers \(m\) and \(n\) by \((m, n)\). The notion of prime labeling introduced by Entringer and appeared in [4] by Tout, Dabboucy and Howalla in \(1982\). A graph \(G\) with vertex set \(V(G)\) is said to have a prime labeling if there exists a bijective function \(f: V(G) \to\{1,2, \ldots,|V(G)|\}\) such that for every edge \(x y \in E(G), f(x)\) and \(f(y)\) are relatively prime. A graph \(G\) that admits a prime labeling is called a prime graph. The prime labeling of some families of graphs were studied by many authors. Entringer conjectured that all trees have prime labeling. Fu and Huang [5] proved that all complete binary trees are prime. Among the other classes of trees known to have prime labeling are: paths, stars, spiders, olive trees, all trees of order up to \(50,\) palm trees, and banana trees (see [2]).

Seoud and Youssef [6] defined \(R_{n}\) as the maximal prime graph of order \(n\) and denoted to the number of edges in \(R_{n}\) by \(\rho(n)\). They gave an exact formula for \(\rho(n)\) and gave some necessary conditions for a graph to be prime and gave a relation between prime labeling and vertex coloring of graphs. They also conjectured that all unicyclic graphs are prime.

In \(2011,\) Vaidya and Prajapati [7] gave a variation of the definition of prime labeling. They called a graph \(G\) of order \(n\) is \(k-\)prime for some positive integer \(k\) if its vertices can be labeled bijectively by the labels \(k, k+1, \ldots, k+n-1\) such that adjacent vertices receive relatively prime labels. For more details about the known results on prime labelings see [2,8,9,10,11,12,13].

In the following we introduce a new variation of the prime labeling.

Definition 1. A graph \(G\) with vertex set \(V(G)\) is said to have an odd prime labeling if there exists an injective function \(f: V(G) \to\{1,3,5, \ldots, \mid V(G) \mid\}\) such that for every edge \(x y \in E(G)\) \(f(x)\) and \(f(y)\) are relatively prime. A graph \(G\) that admits an odd prime labeling is called an odd prime graph.

We give a generalization of the concept of the prime labeling as follows:

Definition 2. Let \(k\) and \(d\) be positive integers. A graph \(G\) with vertex set \(V(G)\) and of order n is said to have a \((k ,d )-\)prime labeling if there exists an injective function \(f: V(G) \to\{k, k+d, k+2 d,\ldots, k+(n-1) d\} \quad\) such \(\quad\) that \(\quad\) for \(\quad\) every \(\quad\) edge \(x y \in E(G)\), \((f(x), f(y))=1.\) A graph \(G\) that admits a \((k, d)-\)prime labeling is called a \((k, d)-\)prime graph.

With this notation, the \((1,1) -\)prime labeling and the prime labeling coincides; the \((1,2) -\)prime labeling is the same as odd prime labeling and the \((k, 1)-\)prime labeling is the same as the \(k-\)prime labeling. In this paper we deal with the odd prime labeling. We give some necessary conditions for a graph to be odd prime and classify some particular families of graphs according to their prime labeling.

2. Some properties of odd prime graphs

In this section we give some necessary conditions for a graph to be an odd prime.

Theorem 1.

• (i) Every spanning subgraph of an odd prime graph is odd prime graph.
• (ii) Every graph is an induced subgraph of an odd prime graph.

Proof.

• (i) Follows directly from the definition.
• (ii) Let \(G\) be a graph of order \(n \geq 2\) and let \(1< p_{1}< p_{2}< \cdots< p_{n-1}\) be the first \(n-1\) odd prime numbers. As the number of odd integers which are greater than \(1\) and less than \(p_{n-1}\) is equal to \(\dfrac{p_{n-1}-3}{2}\) and the number of odd primes less than \(p_{n-1}\) is equal to \(n-2,\) then the number of composite odd positive integers less than \(p_{n-1}\) is equal to \(\dfrac{p_{n-1}-3}{2}-(n-2)=\dfrac{p_{n-1}+1}{2}-n\). Now label the vertices of \(G\) distinctly by \(1, p_{1}, p_{2}, \cdots, p_{n-1}\). Then add \(m\) isolated vertices to \(G,\) where \(m=\dfrac{p_{n-1}+1}{2}-n\). Finally label these isolated vertices distinctly from \(\left\{2 k+1: 1< 2 k+1< p_{n-1}\right\} \backslash\left\{1, p_{1}, p_{2}, \cdots, p_{n-1}\right\}.\)

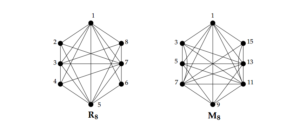
Definition 3. Let \(M_{n}\) be the graph whose vertex set \(V\left(M_{n}\right)=\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}\) and whose edge set \(\quad E\left(M_{n}\right)\) is defined as \(v_{i} v_{j} \in E\left(M_{n}\right)\) if and only if \((2 i-1,2 j-1)=1,\) for every \(v_{i}, v_{j} \in V\left(M_{n}\right)\) and \(i< j .\) We call \(M_{n},\) the maximal odd prime graph of order \(n .\) We denote the size of \(M_{n}\) by \(\gamma(n)\). It is clear that \(\gamma(n)\) represents the maximum number of edges in the odd prime graph of order \(n\) and any graph of order \(n\) is isomorphic to a spanning subgraph of \(M_{n}\).

Remark 1. One way to obtain the graph \(M_{n}\) is to label the vertices of the complete graph \(K_{n}\) distinctly by the odd integers \(1,3,5, \ldots, 2 n-1\) and then successively delete any edge whose the labels of its end vertices have a common divisor greater than \(1 .\) Then we can get: \(\gamma(2)=1, \gamma(3)=3, \gamma(4)=6, \gamma(9)=1,\) and \(\gamma(6)=14\). Another way to obtain \(M_{n}\) is from \(M_{n-1}\) by adding a new vertex with label \(2 n-1\) to the graph \(M_{n-1}\) such that this vertex is adjacent to a vertex in \(M_{n-1}\) labeled \(2 i-1,1 \leq i \leq n-1\) if \((2 i-1,2 n-1)=1\). Figure 1 shows the maximal prime graph \(R_8\) and the maximal odd prime graph \(M_{8}\).

For a given positive integer \(n\), let \(X_{n}=\{1 \leq k \leq n:(k, n)=1\}\). This gives that \(\phi(n)=\left|X_{n}\right|,\) where \(\phi(n)\) is the Euler's phi function. If \(n\) is odd integer greater than \(1,\) we may decompose \(X_{n}\) into two disjoint subsets as \(X_{n}=O_{n} \cup E_{n},\) where \(O_{n}\) (resp. \(\left.E_{n}\right)\) is the set of all odd (resp. even ) positive integers through 1 to \(n\) which are relatively prime to \(n\). We denote to \(\left|O_{n}\right|\) by \(\phi_{0}(n)\).

In the following lemma we show that both \(O_{n}\) and \(E_{n}\) have the same number of elements if \(n\) is odd integer greater than \(1\).

Lemma 1. If \(n\) is odd integer such that \(n \geq 3,\) then \(\left|O_{n}\right|=\left|E_{n}\right|=\dfrac{\phi(n)}{2}\).

Proof. Since we have \(k \in O_{n}\) if and only if \(n-k \in E_{n},\) we get the result.

The following result gives an exact formula for \(\gamma(n)\).

Theorem 2. If \(n \geq 2,\) then \(\gamma(n)=\dfrac{1}{2} \displaystyle\sum_{i=2}^{n} \phi(2 i-1)\).

Proof. From Remark 1 above, we have for \(n \geq 3, \gamma(n)=\gamma(n-1)+\phi_{0}(2 n-1),\) with \(\gamma(2)=\phi_{o}(3)=1 .\) Solving this recurrence relation we get \(\gamma(n)=\sum^{n} \phi_{0}(2 i-1)\) and the results follows from Lemma 1.

According to the above theorem we get that all graphs of order not exceeding \(7\) are odd prime except \(K_{5}, K_{6},\) and \(K_{7}\).

Seoud and Youssef [6] showed that \(\beta\left(C_{n}^{2}\right)=\left\lfloor {\dfrac{n}{3}} \right\rfloor, n \geq 4 .\) We shall show that if an edge deleted from \(C_{n}^{2}, n \geq 5,,\) then the vertex independence number of the resulting graph is the same as \(C_{n}^{2}\) except the case when \(n \equiv 2(\bmod 3) .\) In the following theorems we study some more properties for the graph \(M_{n}\).

Theorem 3. For \(n \geq 2, \beta\left(M_{n}\right)=\left\lfloor {\dfrac{n+1}{3}} \right\rfloor,\) where \(\beta(G)\) is the vertex independence number of a graph \(G\).

Proof. If \(2 \leq n \leq 4,\) we have \(M_{n}=K_{n}\) and the results follow. For \(n \geq 5,\) consider the graph \(G=C_{n}^{2}-e\) with vertex set \(\mathrm{V}(G)=\left\{v_{1}, v_{2}, \ldots, v_{n}\right\}\) and edge set \(E(G)=\left\{v_{i} v_{j}: i-j \equiv \pm 1(\bmod n)\right\} \cup\left\{v_{i} v_{i+2}: 1 \leq i \leq n-2\right\} \cup\left\{v_{n} v_{2}\right\} .\) We claim that \(G\) is odd prime graph with \(\beta(G)=\left\lfloor {\dfrac{n+1}{3}} \right\rfloor.\) Define a function \(f: \Gamma(G) \to\{1,3,5, \ldots, 2 n-1\}\) in three cases according to \(n\) modulo 3 as follows:

If \(n \equiv 0(\bmod 3)\)

\[\begin{array}{ll} f\left(v_{3{i-2}}\right)=3(2 i-1), & 1 \leq i \leq \dfrac{n}{3}, \\[2mm] f\left(v_{3{i-1}}\right)=3(2 i-1)-2, & 1 \leq i \leq \dfrac{n}{3}, \\[2mm] f\left(v_{3{i}}\right)=3(2 i-1)+2, & 1 \leq i \leq \dfrac{n}{3}. \end{array} \] If \(n \equiv 1(\bmod 3)\) \[\begin{array}{ll} f\left(v_{3{i-2}}\right)=3(2 i-1), & 1 \leq i \leq \dfrac{n-1}{3}, \\[2mm] f\left(v_{3{i-1}}\right)=3(2 i-1)-2, & 1 \leq i \leq \dfrac{n-1}{3},\\[2mm] f\left(v_{3{i}}\right)=3(2 i-1)+2, & 1 \leq i \leq \dfrac{n-1}{3},\\[2mm] f\left(v_{3{n}}\right)=2n-1. \end{array} \] If \(n \equiv 2(\bmod 3)\) \[\begin{array}{ll} f\left(v_{3{i-2}}\right)=3(2 i-1), & 1 \leq i \leq \dfrac{n+1}{3}, \\[2mm] f\left(v_{3{i-1}}\right)=3(2 i-1)-2, & 1 \leq i \leq \dfrac{n+1}{3}, \\[2mm] f\left(v_{3{i}}\right)=3(2 i-1)+2, & 1 \leq i \leq \dfrac{n-2}{3}. \end{array} \] For \(1\leq i \leq \left\lfloor {\dfrac{n}{3}} \right\rfloor\), we have \begin{equation*} \begin{aligned} \left(f\left(v_{3i-2}\right), f\left(v_{3i-1}\right)\right)&=(3(2 i-1), 3(2 i-1)-2)=1, \\ \left(f\left(v_{3i-1}\right), f\left(v_{3 i}\right)\right)&=(3(2 i-1)-2,3(2 i-1)+2)=1,\\ \left(f\left(v_{3 i-2}\right), f\left(v_{3 i}\right)\right)&=(3(2 i-1), 3(2 i-1)+2)=1. \end{aligned} \end{equation*} Checking the relativelilty prime of the other vertices, showing that the graph \(G\) is odd prime with. For \(n \equiv 2(\bmod 3),\) the set \(\left\{v_{1}, v_{4}, v_{7}, \ldots, v_{n-1}\right\}\) is the maximal independent set in the graph \(G .\) For the other cases we have \(\beta(G)=\beta\left(C_{n}^{2}\right) .\) That is in all cases we have \( \beta(G)=\left\lfloor {\dfrac{{n + 1}}{3}} \right\rfloor . \)

Now, as \(G\) is odd prime, then

For the other side of the inequality, since the set \(\left\{v_{i} \in V\left(M_{n}\right): \quad 1 \leq i \leq n, 3 \mid i\right\}\) is an independent set of vertices in \(M_{n},\) then From (1) and (2), the result follows.

The proof of the following theorem is similar to a proof given by Youssef [15], which concerns the prime labeling.

Theorem 4. For \(n\leq 2,\)

• (i) \(\omega\left(M_{n}\right)=\pi(2 n-1),\) where \(\omega(G)\) is the vertex clique number of a graph \(G\)
• (ii) \(\chi\left(M_{n}\right)=\pi(2 n-1)\), where \(\chi(G)\) is the chromatic number of a graph \(G\).

Proof.

• (i) Let \(p_{1}< p_{2}< \cdots< p_{\pi(2 n-1)}\) be the list of all odd prime numbers \(\leq 2 n-1\), then the induced subgraph of \(M_{n}\) generated by \(U=\left\{v_{i} \in V\left(M_{n}\right): i=1\right.\) or \(i=p_{j}\) for some \(\left.1 \leq j \leq \pi(2 n-1)\right\}\) is the graph \(K_{\pi(2 n-1)},\) hence \(\omega\left(M_{n}\right) \geq \pi(2 n-1) .\) Conversely, for \(1 \leq i \leq \pi(2 n-1)-1\) define, \(\displaystyle V_{i}=\left\{v_{j} \in V\left(M_{n}\right): p_{i} \mid j\right\},\) then \(V(G)=\displaystyle\left\{v_{1}\right\} \cup \bigcup_{i=1}^{\pi(2 n-1)-1} V_{i}=\left\{v_{1}\right\} \cup \bigcup_{i=1}^{\pi(2 n-1)-1}\left(V \backslash \bigcup_{ j< i} V_{j}\right)\) is a partition of \(V\left(M_{n}\right)\) into independent sets and let \(K_{\omega\left(M_{n}\right)}\) be a maximal complete subgraph of \(M_{n},\) then for \(\displaystyle 1 \leq i \leq \pi(2 n-1)-1,\left|V\left(K_{\omega\left(M_{n}\right)}\right) \cap\left(V \backslash \bigcup_{ j< i} V_{j}\right)\right| \leq 1,\) hence \(\left|V\left(K_{\omega\left(M_{n}\right)}\right)\right| \leq \pi(2 n-1),\) that is \(\omega\left(M_n\right)\leq \pi (2n-1).\)
• (ii) An argument similar to that in part \((i)\) shows that \(\chi(M_n)=\pi(2n-1)\).

The following corollary due to Theorem 3 and Theorem 4 gives some necessary conditions for a graph to be an odd prime graph.

Corollary 1. If \(G\) is an odd prime graph of order \(n\), then

• (i) \(\left| {E\left( G \right)} \right| \le \gamma \left( n \right),\)
• (ii) \(\beta \left( G \right) \ge \left\lfloor {\dfrac{{n + 1}}{3}} \right\rfloor ,\)
• (iii) \(\omega(G)\leq \pi (2n-1),\)
• (iv) \(\chi (G)\leq \pi (2n-1)\).

Proof. If \(G\) is an odd prime graph of order \(n\), then \(G\) is a spanning subgraph of \(M_{n}\). That is \(G \subseteq M_{n}\) and the results follow.

3. Odd prime labeling of some special graphs

In this section we deal with the odd prime labeling of some special graphs. The cycle \(C_{n}\) is odd prime for every \(n \geq 3,\) while the following result concerns \(K_{n}\).

Theorem 5. For \(n \geq 2, K_{n}\) is odd prime for every \(n \leq 4\).

Proof. If \(2 \leq n \leq n,\) we label the vertices of \(K_{n}\) by the numbers \(1,3, \ldots, 2 n-1 .\) Conversely, if \(n \geq 5,\) we have \(\beta \left( {{K_n}} \right) = 1 < \left\lfloor {\dfrac{{n + 1}}{3}} \right\rfloor \) and the graph is not odd prime by Corollary 1(ii).

Although the wheel \(W_{n}\) is prime if and only if \(n\) is even, we prove that all wheels are odd prime.

Theorem 6. \(\mathrm{W}_{n}\) is odd prime for every \(n \geq 3\).

Proof. Let \(V\left(W_{n}\right)=\left\{u_{0}, u_{1}, u_{2}, \ldots, u_{n}\right\},\) where \(u_{0}\) is the center vertex and let \(E\left(W_{n}\right)=\left\{u_{0} u_{i}: 1 \leq i \leq n\right\} \cup\left\{u_{i} u_{j}: j-i \equiv \pm 1(\bmod n)\right\}\).

Let \(f: V\left(W_{n}\right) \to \{1,3,5, \ldots, 2 n+1\}\). We have two cases to consider:

Case 1: \(n \not\equiv 1(\bmod 3)\)

Define \(f\) as follows: \(f\left(u_{i}\right)=2 i+1, \quad 0 \leq i \leq n\). As any integer is relatively prime to \(1\) and any two consecutive odd integers are relatively prime, we have to check only the relativity prime of \(f\left(u_{1}\right)\) and \(f\left(u_{n}\right) .\) We have \(\left(f\left(u_{1}\right), f\left(u_{n}\right)\right)=(3,2 n+1)=1,\) since \(2 n+1 \not\equiv 0(\bmod 3)\). Hence \(f\) is an odd prime labeling of \(W_{n}\) in this case.

Case 2: \(n \equiv 1(\bmod 3)\).

Define \(f\) as \(f\left(u_{i}\right)=2 i+1, \quad 0 \leq i \leq n-2, \quad f\left(u_{n-1}\right)=2 n+1, \quad\) and \(\quad f\left(u_{n}\right)=2 n-1\). We can easily check again that \(f\) is an odd prime labeling of \(W_{n}\) in that case.

Theorem 7. \(H_{n}\) is odd prime for every \(n \geq 3\).

Proof. Let \(V\left(H_{n}\right)=\left\{u_{o}, u_{1}, u_{2}, \ldots, u_{n}\right\} \cup\left\{v_{1}, v_{2}, \ldots, v_{n}\right\},\) where \(u_{o}\) is the center vertex and let \[ E\left(H_{n}\right)=\left\{u_{o} u_{i}: 1 \leq i \leq n\right\} \cup\left\{u_{i} u_{j}: i-j \equiv \pm 1(\bmod n)\right\} \cup\left\{u_{i} v_{i}: 1 \leq i \leq n\right\}\,. \] Let \(f: V\left(H_{n}\right) \to\{1,3,5, \ldots, 4 n+1\} .\) We have two cases to consider:

Case 1: \(n \not\equiv 1(\bmod 3)\). Define \(f\) as follows

\[ \begin{aligned} f\left(u_{o}\right)&=1, \\ f\left(u_{i}\right)&=4 i-1, \quad 1 \leq i \leq n, \\ f\left(v_{i}\right)&=4 j+1, \quad 1 \leq j \leq n. \end{aligned} \] As any integer is relatively prime to 1 and any two consecutive odd integers are relatively prime. Also \(\left(f\left(u_{i}\right), f\left(u_{i+1}\right)\right)=1, \quad 1 \leq i \leq n-1\) and \(\left(f\left(u_{1}\right), f\left(u_{n}\right)\right)=(3,4 n-1)=1,\) since \(4 n-1 \not\equiv 0(\bmod 3) .\) Hence \(f\) is an odd prime labeling of \(H_{n}\) in this case.

Case 2: \(n \equiv 1(\bmod 3)\). Define \(f\) as follows:

\[ \begin{aligned} f\left(u_{1}\right)&=1, & & \\ f\left(u_{i}\right)&=4 i-1, & 1 \leq i \leq n-1,& & f\left(u_{n}\right)=4 n+1,& \\ f\left(v_{j}\right)&=4 j+1, & 1 \leq j \leq n-1,& & f\left(v_{n}\right)=4 n-1.& \end{aligned} \] As in Case 1, it remains to check \(\left(f\left(u_{1}\right), f\left(u_{n}\right)\right)\) and \(\left(f\left(u_{n-1}\right), f\left(u_{n}\right)\right).\) Now \[\left(f\left(u_{1}\right), f\left(u_{n}\right)\right)=(3,4 n+1)=1, \;\text{since}\; 4 n+1 \equiv 2(\bmod 3), \] and \[\left(f\left(u_{n-1}\right), f\left(u_{n}\right)\right)=(4 n-5,4 n+1)=(4 n-5,6)=1,\; \text{since}\;4 n-5 \equiv 2(\bmod 3) . \] Thus \(f\) is an odd prime labeling of \(H_{n}\) in that case also.

It is clear that \(K_{1, n}, n \geq 1\) is odd prime for every \(n \geq 1\) and Bertrand's Postulate [3] guarantees the odd prime labeling of \(K_{2, n}\), \(n \geq 2\). Although the smallest values of \(m\) and \(n\) for which \(K_{m, n}\) is not prime is \((m, n)=(3,3)\), however, we show in the following results that the smallest values of \(m\) and \(n\) for which \(K_{m, n}\) is not odd prime is \((m, n)=(7,7)\). The proof of the result is similar to the one given by Fu and Huang [5] and therefore we omit it.

Theorem 8. \(K_{m, n}\), \(3 \leq m \leq n\) is odd prime if and only if \(m \leq \pi(2 m+2 n-1)-\pi\left(\dfrac{2 m+2 n-1}{3}\right)+1.\)

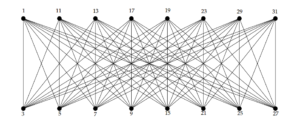
According to the above theorem and the odd prime labeling of \(K_{1, n}\) and \(K_{2, n}\), we can find that for \(2\le m+n\le 20\), \(K_{m,n}\) is odd prime if and only if \((m,n)\neq(7,7)\), \((8,9)\), \((8,10)\), \((9,9)\), \((9,10)\), \((8,12)\), \((9,11)\), and \((10,10)\). Figure 2 shows the odd prime labeling of the complete bipartite graph \(K_{8,8}\)

In 2002, Vilfred et al., [13] conjectured that all ladders \(L_{n}\) are prime. This conjectured was proved in \(2015\) by Dean [8], however in the next theorem we prove that all ladders have odd prime labeling.

Theorem 9. \(L_{n}\) is odd prime for every \(n \geq 1\).

Proof. Let \(V\left(L_{n}\right)=\left\{u_{1}, u_{2}, \ldots, u_{n}\right\} \cup\left\{v_{1}, v_{2}, \ldots, v_{n}\right\},\) and \(E\left(L_{n}\right)=\left\{u_{i} u_{i+1}: 1 \leq i \leq n-1\right\} \cup\left\{v_{i} v_{i+1}: 1 \leq i \leq n-1\right\} \cup\left\{u_{i} v_{i}: 1 \leq i \leq n\right\}.\) Let \(f: V\left(L_{n}\right) \to \{1,3,5, \ldots, 4 n-1\}\) be defined as \[f\left(u_{i}\right)=4 i-3, \quad 1 \leq i \leq n, \quad f\left(v_{j}\right)=4 j-1, \quad 1 \leq j \leq n. \] We have \[ \begin{aligned} \left(f\left(u_{i}\right), f\left(u_{i+1}\right)\right)&=(4 i-3,4 i+1)=(4 i-3,4)=1,& &1 \leq i \leq n-1,&\\ \left(f\left(v_{i}\right), f\left(v_{i+1}\right)\right)&=(4 i-1,4 i+3)=(4 i-1,4)=1,& &1 \leq i \leq n-1,&\\ \left(f\left(u_{i}\right), f\left(v_{i}\right)\right)&=(4 i-3,4 i-1)=(4 i-3,2)=1,& &1 \leq i \leq n.& \end{aligned} \] Hence \(f\) is an odd prime labeling.

Theorem 10. \(T_2 (n)\) is odd prime for every \(n\ge 2\).

Proof. Let the vertices of the ith level of \(T_{2}(n)\) be \(v_{i, 1}, v_{i, 2}, v_{i, 3} \cdots, v_{i, 2^{i}}\) where \(1 \leq i \leq n .\) Define a labeling function \(f\left(V\left(T_{2}(n)\right)\right) \to\left\{1,3, \ldots, 2^{n+1}-3\right\}\) as follows: \[ f\left(v_{p, q}\right)=\left\{\begin{aligned} &1,& & \text { if } p=n, q=2^{n-1},& \\ &(2 q-1)^{n+1-p}+1,& &\text { otherwise }.& \end{aligned}\right. \] To prove that this function is an odd labeling, we note that each vertex in a level \(p,\) say the vertex \(v_{p, q},\) is adjacent to the two vertices \(v_{p+1,2 q-1}\) and \(v_{p+1,2 q}\) where \(1 \leq p< n\). So we have to show that \(\left(f\left(v_{p, q}\right), f\left(v_{p+1,2 q-1}\right)\right)=1\) and \(\left(f\left(v_{p, q}\right), f\left(v_{p+1,2 q}\right)\right)=1\). For the first, we have \[ \begin{aligned} \left(\left(f\left(v_{p, q}\right), f\left(v_{p+1,2 q-1}\right)\right)\right.&=\left((2 q-1) 2^{n+1-p}+1,(4 q-3) 2^{n-p}+1\right) \\ &=\left((2 q-1) 2^{n+1-p}-(4 q-3) 2^{n-p},(4 q-3) 2^{n-p}+1\right) \\ &=\left(2^{n-p}((2 q-1) 2-(4 q-3)),(4 q-3) 2^{n-p}+1\right) \\ &=\left(2^{n-p},(4 q-3) 2^{n-p}+1\right)=1. \end{aligned} \] The second one can be treated similarly.

4. Odd prime labeling of disjoint union of graphs

The graph \(C_{m} \cup C_{n}\) is prime if and only if \(m\) or \(n\) is odd. However, we prove in the following theorem that the disjoint union of any two cycles is odd prime.

Theorem 11. \(\mathrm{C}_{m} \cup \mathrm{C}_{n}\) is odd prime for all \(m, n \geq 3\).

Proof. If \(m \not\equiv 1(\bmod 3)\), we label the vertices of \(C_{m}\) and \(C_{n}\) successively by the labels \(3,5,7, \ldots, 2 m+1\) and \(1,2 m+3,2 m+5, \ldots, 2 m+2 n-1 \) respectively. Otherwise, if \( m \equiv 1(\bmod 3)\), we label the vertices the vertices of \(C_{m}\) and \(C_{n}\) successively by the labels \(3,5,7, \ldots, 2 m-1,2 m+3\) and \( 1,2 m+1,2 m+5,2 m+7, \ldots, 2 m+2 n-1\) respectively. The reader can check easily that the graph is odd prime in the two cases.

Theorem 12. \(K_{m} \cup K_{m}\), \(m \leq n\) is odd prime if and only if \(m+n \leq 7\).

Proof. Necessity, let \(m+n>7\). Since \(\left\lfloor {\dfrac{{m + n + 1}}{3}} \right\rfloor \ge 3 > \beta \left( {{K_m} \cup {K_m}} \right) = 2\), then \(K_{m} \cup K_{m}\) is not odd prime. Sufficiency, let \(m+n \leq 7\), \(m \leq n\) and \(V\left(K_{m} \cup K_{m}\right)=\left\{x_{1}, x_{2}, \ldots, x_{m}\right\} \cup\left\{y_{1}, y_{2}, \ldots, y_{n}\right\}\). Define \(f: V\left(K_{m} \cup K_{m}\right) \to\{1,3, \ldots, 2 m+2 n-1\}\) as \[f\left(x_{i}\right)=2 i+1, \quad 1 \leq i \leq m, \quad f\left(y_{j}\right)=2 m+2 j+1, \quad 1 \leq i \leq m-1, \text{ and } f\left(y_{n}\right)=1. \] Since all positive odd integers not exceeding \(13\) except the integer \(3\) or \(9\) are pairwise relatively prime and since we put the label \(3\) in only one component as \(m\le 3\), this guarantees that \(f\) is an odd prime labeling of \(K_{m} \cup K_{m}\). This completes the proof.

Theorem 13. If \(G\) is odd prime graph of order \(n\), then \(G \cup P_{m}\) is odd prime.

Proof. Let \(V\left(P_{m}\right)=\left\{u_{1}, u_{2}, \ldots, u_{m}\right\}\) and \(f\) be an odd prime labeling for the graph \(G .\) Define a labeling \(g: V\left(G \cup P_{m}\right) \to\{1,3,5, \ldots, 2 n+2 m-1\}\) as follows: \(g(v)=f(v)\) for every vertex \(v \in V(G)\) and \(g\left(u_{i}\right)=2 n+2 i-1\), \(1 \leq i \leq m\). As every two consecutive odd integers are relatively prime, the result follows.

The following result shows that the disjoint union of any number of paths is odd prime.

Corollary 2. \(\displaystyle\bigcup_{i=1}^{n} P_{m_{i}}\) is odd prime.

Theorem 14. If \(G\) is odd prime graph of order \(n\), then \(G \cup K_{3}\) is odd prime.

Proof. Let \(V\left(K_{3}\right)=\left\{u_{1}, u_{2}, u_{3}\right\}\) and \(f\) be an odd prime labeling for the graph \(G .\) Define a labeling \(g: V\left(G \cup P_{m}\right) \to\{1,3,5, \ldots, 2 n+2 m-1\}\) as follows: \(g(v)=f(v)\) for every vertex \(v \in V(G)\) and \(g\left(u_{i}\right)=2 n+2 i-1\), \(1 \leq i \leq 3 .\) As every three consecutive odd integers are pairwise relatively prime, the result follows.

Corollary 3. \(mK_{3}\) is odd prime for every \(m \geq 1\).

The above theorem can be generalized by substitute \(K_3\) by the graph \(C_{2^m+1}\) for every positive integer \(m\).

Theorem 15. For \(m\ge 1\) and \(n\ge 2\), \(mK_n\) is odd prime if and only if (\(m \ge 1\) and \(n= 2\) or \(3\)) or (\(m= 1\) and \(n= 4\)).

Proof. Necessity, if \((m \geq 1\) and \(n \geq 5)\) or \((m \geq 2\) and \(n=4),\) we have \(\left\lfloor {\dfrac{{mn + 1}}{3}} \right\rfloor > m = \beta \left( {m{K_n}} \right).\) Then the graph is not odd prime by Corollary 1(ii). Sufficiency comes by Corollary 2 and Corollary 3.

Comment

In this paper, we showed that some families of graphs like \(K_{4}, W_{2 n+1},\) and \(C_{2 m+1} \cup C_{2 n+1}\) are odd prime, although they are not prime. Thus there are odd prime graphs that are not prime. You might have already asked whether the converse is true. That is there are prime graphs that are not prime? We expect that the answer is no and formalize this in the following conjecture.

Conjecture 1. Every prime graph is odd prime graph.

Authorcontributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflictofinterests

The authors declare no conflict of interest.