Open Journal of Discrete Applied Mathematics
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2020.0042
The rank of Pseudo walk matrices: controllable and recalcitrant pairs
Alexander Farrugia
Department of Mathematics, University of Malta Junior College, Msida, Malta.; alex.farrugia@um.edu.mt; Tel.: +35625907254
Abstract
Keywords:
1. Preliminaries
Let \(G\) be a simple graph with vertex set \(\mathit{V}({G})=\{1,2,\ldots,n\}\), having neither loops nor multiple edges. The adjacency matrix \(\mathbf{A}\) is the \(n\times n\) matrix whose \(ij^{th}\) entry is \(1\) if vertices \(i\) and \(j\) are connected by an edge and is \(0\) otherwise.
Let \(\mathbf{I}\) denote the identity matrix. The \(k^{th}\) column of \(\mathbf{I}\) is \(\mathbf{e}_k\) for all \(k\). The characteristic polynomial \(|x\mathbf{I}-\mathbf{A}|\) of \(\mathbf{A}\), denoted by \(\phi(G,x)\), is a monic polynomial with integer coefficients. Since the edges of \(G\) are undirected, \(\mathbf{A}\) is symmetric and the roots of \(\phi(G,x)\), which are the eigenvalues of \(\mathbf{A}\) (or of \(G\)), are real numbers. Thus, the eigenvalues of \(G\) are \(n\) totally real algebraic integers, with possible repetitions. A simple eigenvalue is a simple root of \(\phi(G,x)\). As we shall see in the next sections, we shall be focusing on the \(s\) distinct eigenvalues \(\lambda_1>\ldots>\lambda_s\) of \(G\), largely ignoring their multiplicities. To this end, if \(\phi(G,x)=\prod_{k=1}^s (x-\lambda_k)^{q_k}\), where \(q_k\) is the multiplicity of \(\lambda_k\) for all \(k\), then we denote the product of distinct factors \(\prod_{k=1}^s (x-\lambda_k)\) by \(m(G,x)\). Since \(\mathbf{A}\) is symmetric, it is diagonalizable; thus, \(m(G,x)\) is the matrix minimal polynomial of \(\mathbf{A}\).
By differentiating \(\prod_{k=1}^s (x-\lambda_k)^{q_k}\) with respect to \(x\) to obtain \(\phi^\prime(G,x)\), we discover that \(\lambda\) is a multiple root of \(\phi(G,x)\) if and only if it is also a root of \(\phi^\prime(G,x)\). Thus, we have the following theorem.
Theorem 1. \(m(G,x)=\phi(G,x)\) if and only if \(\phi(G,x)\) and \(\phi^\prime(G,x)\) have no common polynomial factors.
In this paper, we propose to consider the factorization of the minimal polynomial \(m(G,x)\) over \(\mathbb{Q}\), rather than that over \(\mathbb{R}\), the latter of which yields the distinct eigenvalues of \(G\). This will reveal a restriction on the possible values of the rank of any walk matrix of \(G\).
The rest of the paper is structured as follows. The next section shall present elementary results on minimal polynomials of roots of \(m(G,x)\). Section 3 reminds the reader of the basic results on walks of graphs, then presents the concepts of pseudo walk matrices and their walk vectors, originally introduced in [1]. The following section mentions the important results from that paper that relate to pseudo walk matrices, which leads to the significant result in Theorem 12 that restricts the matrix rank of any pseudo walk matrix to a few possible values depending on the factorization of \(m(G,x)\).
Section 5 provides a brief preliminary on the control theoretic aspects relevant to this paper, leading to the justification for generalizing controllable pairs \((\mathbf{A},\mathbf{v})\) to the case where \(\mathbf{v}\) is a walk vector. The next section focuses on graphs having an irreducible characteristic polynomial, which are shown to occur relatively frequently. For such graphs, it is proved that \((\mathbf{A},\mathbf{v})\) is controllable for all walk vectors \(\mathbf{v}\). Further interesting results on controllable pairs are provided in Section 7. The final section introduces recalcitrant pairs, which, in a sense, are the direct opposite of controllable pairs because they occur when the rank of a pseudo walk matrix attains the lower bound set by Theorem 12. Several related results on recalcitrant pairs are revealed.
2. Minimal polynomials of eigenvalues
A polynomial \(p(x)\) with integer coefficients (of positive degree) is called primitive if its coefficients have no common integer factors other than \(\pm 1\). Since both \(m(G,x)\) and \(\phi(G,x)\) are monic, they are clearly both primitive. The following lemma tells us that monic polynomials with coefficients in \(\mathbb{Q}\) must have integer coefficients whenever their product has integer coefficients.Lemma 1. Let \(p_1(x)\) and \(p_2(x)\) be two monic polynomials with rational coefficients, both having degree at least one. Suppose \(p(x)=p_1(x)\,p_2(x)\) is a monic polynomial with integer coefficients. Then the coefficients of both \(p_1(x)\) and \(p_2(x)\) are integers.
Proof. Rewrite \(p_1(x)\) and \(p_2(x)\) as \(\frac1{a}(a\,p_1(x))\) and \(\frac1{b}(b\,p_1(x))\) respectively, where the integers \(a\) and \(b\) are chosen such that \(a\,p_1(x)\) and \(b\,p_2(x)\) are primitive polynomials with integer coefficients. By Gauss' Lemma [2], the product \((a\,p_1(x))(b\,p_2(x))\), or \((ab)\,p(x)\), is also primitive. But \(p(x)\) is a monic polynomial with integer coefficients; consequently, it is primitive itself. This is only possible if \(ab=\pm 1\). Hence \(p_1(x)\) and \(p_2(x)\) actually have integer coefficients, as required.
Theorem 2. If \(f(x)\), a polynomial with rational coefficients, is a factor of a monic polynomial with integer coefficients, then \(f(x)\) is monic and has integer coefficients.
Even though Theorem 2 appears to be basic, it will have important implications later on in this paper.
Let us consider the minimal polynomial (in field theory) of each eigenvalue \(\lambda_k\) of \(\mathbf{A}^{1}\). This paper requires the reader to distinguish between the minimal polynomial of \(\mathbf{A}\), denoted by \(m(G,x)\), and the minimal polynomial of each eigenvalue \(\lambda_k\). The fact that mathematics uses the same terminology for both is unfortunate. For all eigenvalues \(\lambda_k\), this is the (monic) polynomial \(p_k(x)\) with integer coefficients having the smallest possible degree that satisfies \(p_k(\lambda_k)=0\). The algebraic conjugates of \(\lambda_k\) are all the roots of its minimal polynomial, including \(\lambda_k\) itself. Thus, the conjugates of \(\lambda_k\) are also eigenvalues of \(\mathbf{A}\), otherwise \(m(G,x)\) would not have integer coefficients.
Thus, we decompose the set of distinct eigenvalues \(\Lambda=\{\lambda_1,\ldots,\lambda_s\}\) into \(r\) mutually disjoint subsets \(\Lambda_1,\ldots,\Lambda_r\). Two eigenvalues are in the same set \(\Lambda_i\) if and only if they are algebraic conjugates. We note that, for all \(i\), \(|\Lambda_i|\), the cardinality of set \(\Lambda_i\), is the degree of the minimal polynomial shared by each of its elements; in particular, \(\Lambda_i\) has only one element if and only if its element is an integer. We define the minimal polynomial of \(\Lambda_i\) (for some \(i\)) to be that of any of its elements; we denote this by \(m(\Lambda_i)\). Thus, at worst, \(r=s\) and \(\Lambda\) would be split into \(s\) singletons \(\Lambda_1=\{\lambda_1\},\ldots,\Lambda_s=\{\lambda_s\}\). This happens when all the distinct eigenvalues of the graph \(G\) are integers, in which case \(G\) is an integral graph [3, Section 8.4]. At the other end of the spectrum, \(r\) could be equal to \(1\) and \(m(G,x)\) would then be irreducible over \(\mathbb{Q}\). In this case, all the \(s\) eigenvalues are conjugates, and we only have one set \(\Lambda_1=\{\lambda_1,\ldots,\lambda_s\}\). We shall focus on this case in Section 6, as it seems to be quite common.
Example 1. The eigenvalues of the adjacency matrix of the cycle \(C_7\) on seven vertices are \(\Lambda=\{2,1.247,-0.445,-1.802\}\), all of which are repeated twice except for the eigenvalue \(2\). The characteristic polynomial of \(C_7\) is \(x^7-7x^5+14x^3-7x-2\), which factorizes into \((x-2)(x^3+x^2-2x-1)^2\). Thus \(m(C_7,x)=(x-2)(x^3+x^2-2x-1)=x^4-x^3-4x^2+3x+2\). Hence \(m(\Lambda_1)=x-2\) and \(m(\Lambda_2)=x^3+x^2-2x-1\). Moreover, the set \(\Lambda\) decomposes into \(\Lambda_1=\{2\}\) and \(\Lambda_2=\{1.247,-0.445,-1.802\}\).
3. Walks and Pseudo walk matrices
A walk of length \(\ell\) on \(G\), starting from vertex \(j\) and ending at vertex \(k\), is a sequence of \(\ell+1\) vertices \(v_1,v_2,\ldots,v_{\ell+1}\) (not necessarily distinct) such that \(v_1=j\), \(v_{\ell+1}=k\) and every two consecutive vertices in the sequence are connected by an edge in \(G\).Let \(S\) be any subset of the Cartesian product \(\mathcal{V}^2=\mathcal{V}(G)\times\mathcal{V}(G)\). If \(u=(j,k)\in S\), then \(w_\ell(\{u\})\) is the number of walks of length \(\ell\) in \(G\) that start at \(j\) and end at \(k\). It is well-known that
Since the matrix inverse \((\mathbf{I}-x\mathbf{A})^{-1}\) may be expanded into the formal power series \(\sum_{j=0}^\infty \mathbf{A}^jx^j\), the entry \(\left[(\mathbf{I}-x\mathbf{A})^{-1}\right]_{jk}\), or \(\mathbf{e}_k^{T}(\mathbf{I}-x\mathbf{A})^{-1}\mathbf{e}_j\), can be written as the formal power series \(w_0+w_1x+w_2x^2+w_3x^3+\cdots\), where \(w_0,w_1,w_2,\ldots\) are, respectively, the number of walks of length \(0,1,2,\ldots\) starting from vertex \(j\) and ending at vertex \(k\). Thus, for any \(S\subseteq\mathcal{V}^2\), \[\sum_{(j,k)\in S}\!\!\left[(\mathbf{I}-x\mathbf{A})^{-1}\right]_{jk}=w_0(S)+(w_1(S))x+(w_2(S))x^2+\cdots.\]
In particular, if \(S=V_1\times V_2\), where \(V_1\) and \(V_2\) are both subsets of \(\mathcal{V}(G)\), then the left hand side of the above relation would be simply \(\mathbf{b}_1^{T}(\mathbf{I}-x\mathbf{A})^{-1}\mathbf{b}_2\), where \(\mathbf{b}_1\) is the \(0\)-\(1\) vector where, for all \(k\), its \(k^{th}\) entry is equal to \(1\) if and only if \(k\in V_1\), and \(\mathbf{b}_2\) is defined analogously for \(V_2\). We say that each of \(\mathbf{b}_1\) and \(\mathbf{b}_2\) is an indicator vector for \(V_1\) and \(V_2\) respectively.
In the literature, the walk matrix \(\mathbf{W}\) of \(G\) is generally taken to be the \(n\times n\) matrix where, for all \(k\), its \(k^{th}\) column is the vector \(\mathbf{A}^{k-1}\mathbf{j}\), where \(\mathbf{j}\) is the \(n\times 1\) vector of all ones [4,5,6]. By (1) and (2), \(\left[\mathbf{W}\right]_{jk}=w_{k-1}(S_j)\), where \(S_j=\{j\}\times\mathcal{V}(G)\). Other authors additionally consider walk matrices of the form \(\mathbf{W}_\mathbf{b}=\begin{pmatrix}\mathbf{b} & \mathbf{A}\mathbf{b} & \mathbf{A}^2\mathbf{b} & \cdots & \mathbf{A}^{n-1}\mathbf{b}\end{pmatrix}\), where \(\mathbf{b}\) is any \(0\)-\(1\) vector [1,7,8]. The \(jk^{th}\) entry of \(\mathbf{W}_\mathbf{b}\) is equal to \(w_{k-1}(S^\prime_j)\), where \(S^\prime_j=\{j\}\times B\) and \(B\) is the subset of \(\mathcal{V}(G)\) such that \(\mathbf{b}\) is its indicator vector.
It is clear that
In this paper, we go even further, considering Hankel matrices whose \(jk^{th}\) entry is \(w_{j+k-2}(S)\), where \(S\) is any subset of \(\mathcal{V}^2\). The author of this paper had considered such matrices in [1]. In that paper, it was proved that for any \(S\), there exists a vector \(\mathbf{v}\) (indeed, often more than one) such that the Gram matrix of the columns \(\mathbf{v},\mathbf{A}\mathbf{v},\mathbf{A}^2\mathbf{v},\ldots,\mathbf{A}^{n-1}\mathbf{v}\) is the Hankel matrix \(\mathbf{H}_\mathbf{v}\) whose constant skew diagonal entries are \(w_0(S),w_1(S),\ldots,w_{2n-2}(S)\). The matrix \(\mathbf{W}_\mathbf{v}=\begin{pmatrix}\mathbf{v} & \mathbf{A}\mathbf{v} & \mathbf{A}^2\mathbf{v} & \cdots & \mathbf{A}^{n-1}\mathbf{v}\end{pmatrix}\) is called a pseudo walk matrix, because its entries are usually not walk enumerations, even though the matrix \(\mathbf{H}_\mathbf{v}={\mathbf{W}_\mathbf{v}}^{T}\mathbf{W}_\mathbf{v}\), as already mentioned, contains the walk enumerations \(w_0(S),w_1(S),\ldots,w_{2n-2}(S)\) on its constant skew diagonals.
Definition 3 ([1]). A pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) associated with \(S\subseteq\mathcal{V}^2\) is the \(n\times n\) matrix with columns \(\mathbf{v},\mathbf{A}\mathbf{v},\mathbf{A}^2\mathbf{v},\cdots,\mathbf{A}^{n-1}\mathbf{v}\) such that the entries of the Hankel matrix \(\mathbf{H}_\mathbf{v}={\mathbf{W}_\mathbf{v}}^{T}\mathbf{W}_\mathbf{v}\) satisfy \(\left[\mathbf{H}_\mathbf{v}\right]_{ij}=w_{i+j-2}(S)\) for all \(i\) and \(j\). The vector \(\mathbf{v}\) in the previous sentence is a walk vector associated with \(S\). If \(\mathbf{v}\) is a \(0\)-\(1\) vector, then \(\mathbf{W}_\mathbf{v}\) may be simply called a walk matrix associated with \(S\).
It is proved in [1, Theorem 2.1] that any two distinct walk vectors \(\mathbf{v}_1\) and \(\mathbf{v}_2\) associated with a fixed \(S\subseteq\mathcal{V}^2\) produce two different pseudo walk matrices \(\mathbf{W}_{\mathbf{v}_1}\) and \(\mathbf{W}_{\mathbf{v}_2}\) having the same matrix rank. This fact ensures that any walk vector associated with \(S\), no matter how unusual (some walk vectors may even contain imaginary entries) is fine, keeping in mind that the rank of \(\mathbf{W}_\mathbf{v}\) is significant to the controllability aspects of the graph \(G\), as we shall see later in Section 5.
We note that if the rank of \(\mathbf{W}_\mathbf{v}\) is \(R\), then the \(n\times c\) matrix \(\begin{pmatrix}\mathbf{v} & \mathbf{A}\mathbf{v} & \cdots & \mathbf{A}^{c-1}\mathbf{v}\end{pmatrix}\) has rank \(R\) for all \(c\geq R\). This is because, for any vector \(\mathbf{v}\), we may write down the list of vectors \(\mathbf{v},\mathbf{A}\mathbf{v},\mathbf{A}^2\mathbf{v},\ldots,\mathbf{A}^k\mathbf{v}\), stopping this list when the last vector is linearly dependent on the previous ones. When this happens, \(\mathbf{A}^k\mathbf{v}=\sum_{j=0}^{k-1} a_j\mathbf{A}^j\mathbf{v}\) for some scalars \(a_j\). But by premultiplying both sides of this equation by \(\mathbf{A}^i\), for \(i\) a positive integer, we realize that \(\mathbf{A}^{i+k}\mathbf{v}\) may also be written as a linear combination of the vectors \(\mathbf{v},\mathbf{A}\mathbf{v},\ldots,\mathbf{A}^{k-1}\mathbf{v}\). Consequently, we may say that the rank of \(\mathbf{W}_\mathbf{v}\) is the number \(R\) such that the vectors \(\mathbf{v},\mathbf{A}\mathbf{v},\mathbf{A}^2\mathbf{v},\ldots,\mathbf{A}^{R-1}\mathbf{v}\) are linearly independent but the vectors \(\mathbf{v},\mathbf{A}\mathbf{v},\mathbf{A}^2\mathbf{v},\ldots,\mathbf{A}^R\mathbf{v}\) are linearly dependent.
Because of this, in certain papers such as [1,10], walk matrices are not \(n\times n\) matrices but \(n\times R\) matrices, where \(R\) is as defined in the previous paragraph. We distinguish between the \(n\times n\) pseudo walk matrices defined in Definition 3 from these \(n\times R\) pseudo walk matrices by denoting the latter by \(\overline{W}_\mathbf{v}\).
Earlier, we mentioned that, for a pseudo walk matrix of rank \(R\), there must exist scalars \(a_j\) such that \(\mathbf{A}^R\mathbf{v}=\sum_{j=0}^{R-1} a_j\mathbf{A}^j\mathbf{v}\). This may be rewritten as \(\mathbf{A}^R\mathbf{v}=\overline{W}_\mathbf{v}\mathbf{c}\), where \(\mathbf{c}=\begin{pmatrix}a_0 & a_1 & \cdots & a_{R-1}\end{pmatrix}^{T}\). Clearly the matrix \(\begin{pmatrix}\mathbf{A}\mathbf{v} & \mathbf{A}^2\mathbf{v} & \cdots & \mathbf{A}^R\mathbf{v}\end{pmatrix}\) is equal to \(\overline{W}_\mathbf{v}\begin{pmatrix}\mathbf{e}_2 & \mathbf{e}_3 & \cdots & \mathbf{c}\end{pmatrix}\). Alternatively, \(\mathbf{A}\overline{W}_\mathbf{v}=\overline{W}_\mathbf{v}\mathbf{C}_\mathbf{v}\), where the \(R\times R\) matrix \(\mathbf{C}_\mathbf{v}\) is the companion matrix \(\begin{pmatrix}\mathbf{e}_2 & \mathbf{e}_3 & \cdots & \mathbf{c}\end{pmatrix}\) of \(\overline{W}_\mathbf{v}\) [9,10]. By expanding the determinant \(|x\mathbf{I}-\mathbf{C}_\mathbf{v}|\) along its last column using the Laplace determinant expansion, the characteristic polynomial of \(\mathbf{C}_\mathbf{v}\) is seen to be \(x^R-a_{R-1}x^{R-1}-a_{R-2}x^{R-2}-\cdots-a_0\). We denote this polynomial by \(\phi_\mathbf{v}(x)\) and call it the companion polynomial of \(\mathbf{W}_\mathbf{v}\) (or of \(\overline{W}_\mathbf{v}\)). Note that we started this paragraph with the equation \(\left(\mathbf{A}^R-a_{R-1}\mathbf{A}^{R-1}-a_{R-2}\mathbf{A}^{R-2}-\cdots-a_0\mathbf{I}\right)\mathbf{v}=\mathbf{0}\) --- thus, we have the Cayley-Hamiltonian-like result \((\phi_\mathbf{v}(\mathbf{A}))\mathbf{v}=\mathbf{0}\) for any walk vector \(\mathbf{v}\).
In the literature, an eigenvalue is termed main if it has an associated eigenvector that is not orthogonal to \(\mathbf{j}\). Here, we generalize this definition to \(\mathbf{v}\)--main eigenvalues:
Definition 4. An eigenvalue of \(\mathbf{A}\) is \(\mathbf{v}\)-main if it has an associated eigenvector that is not orthogonal to the walk vector \(\mathbf{v}\).
4. Results on the rank of Pseudo walk matrices
The significance of the companion polynomial is the following result. It is only mentioned in [1], but not proved. The proof below follows that of the similar result in [10], there considering only the particular case \(\mathbf{v}=\mathbf{j}\).Theorem 5 ([1]). For any walk vector \(\mathbf{v}\), \(\phi_\mathbf{v}(x)=\prod(x-\lambda_i)\), with the product running over all the \(\mathbf{v}\)-main distinct eigenvalues of \(G\).
Proof. Suppose \(\lambda\) is an eigenvalue of \(G\) having an associated eigenvector \(\mathbf{x}\) that is not orthogonal to \(\mathbf{v}\). Since \(\mathbf{A}\overline{W}_\mathbf{v}=\overline{W}_\mathbf{v}\mathbf{C}_\mathbf{v}\), we have \(\mathbf{x}^{T}\mathbf{A}\overline{W}_\mathbf{v}=\mathbf{x}^{T}\overline{W}_\mathbf{v}\mathbf{C}_\mathbf{v}\), or \(\lambda (\mathbf{x}^{T}\overline{W}_\mathbf{v}) = (\mathbf{x}^{T}\overline{W}_\mathbf{v})\mathbf{C}_\mathbf{v}\). Thus, the vector \((\overline{W}_\mathbf{v})^{T}\mathbf{x}\) is a left eigenvector associated with the eigenvalue \(\lambda\) of \(\mathbf{C}_\mathbf{v}\). Note that \((\overline{W}_\mathbf{v})^{T}\mathbf{x}\ne\mathbf{0}^{T}\), since it is equal to \(\begin{pmatrix}\mathbf{v}^{T}\mathbf{x} & \mathbf{v}^{T}\mathbf{A}\mathbf{x} & \mathbf{v}^{T}\mathbf{A}^2\mathbf{x} & \cdots & \mathbf{v}^{T}\mathbf{A}^{R-1}\mathbf{x}\end{pmatrix}^{T}\), or \(\left(\mathbf{v}^{T}\mathbf{x}\right)\begin{pmatrix}1 & \lambda & \lambda^2 & \cdots & \lambda^{R-1}\end{pmatrix}^{T}\).
Conversely, suppose \(\lambda\) is an eigenvalue of \(\mathbf{C}_\mathbf{v}\) with associated eigenvector \(\mathbf{y}\). We prove that \(\lambda\) is an eigenvalue of \(G\) having an associated eigenvector not orthogonal to \(\mathbf{v}\). Restarting again from \(\mathbf{A}\overline{W}_\mathbf{v}=\overline{W}_\mathbf{v}\mathbf{C}_\mathbf{v}\), \((x\mathbf{I}_n-\mathbf{A})\overline{W}_\mathbf{v}=\overline{W}_\mathbf{v}(x\mathbf{I}_R-\mathbf{C}_\mathbf{v})\), where \(\mathbf{I}_k\) denotes the \(k\times k\) identity matrix. Hence
On the one hand,
We immediately have the following corollary.
Corollary 1 ([1]). For any walk vector \(\mathbf{v}\) associated with the pseudo walk matrix \(\mathbf{W}_\mathbf{v}\), the following four quantities are equal:
- The rank of \(\mathbf{W}_\mathbf{v}\);
- The number of columns of \(\overline{W}_\mathbf{v}\);
- The number of \(\mathbf{v}\)-main eigenvalues of \(G\);
- The degree of \(\phi_\mathbf{v}(x)\).
Theorem 6([1]). The rank of any pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) is at most equal to \(s\), the number of distinct eigenvalues of \(G\). This upper bound is attained by the walk vector \(\mathbf{p}=\sum_{i=1}^n \mathbf{x}_i\), the sum of any set of \(n\) mutually orthonormal eigenvectors associated with the \(n\) (not necessarily distinct) eigenvalues of \(G\). This walk vector \(\mathbf{p}\) is associated with the set \(\{(v,v)\mid v\in\mathcal{V}(G)\}\) counting the number of all closed walks of \(G\).
A nice result in [1, Theorem 2.3] expresses each coefficient of \(\phi_\mathbf{v}(x)\) in terms of the ratio of two determinants.
Theorem 7([1, Theorem 2.3]). The coefficient of \(x^k\) of the polynomial \(\phi_\mathbf{v}(x)\) of degree \(R\) is \((-1)^{R-k}\frac{|\mathbf{N}|}{|\mathbf{H}|}\), where \(\mathbf{H}=\overline{W}_\mathbf{v}^{T}\overline{W}_\mathbf{v}\) and \(\mathbf{N}\) is the matrix whose first \(k\) columns are those of \(\mathbf{H}\) and whose last \(r-k\) columns are those of \(\mathbf{H}^\prime=\overline{W}_\mathbf{v}^{T}\mathbf{A}\overline{W}_\mathbf{v}\).
Clearly the determinants \(|\mathbf{H}|\) and \(|\mathbf{N}|\) in the above theorem are integers, because their entries are walk enumerations on the graph. Hence \(\phi_\mathbf{v}(x)\) has rational coefficients. However, by Theorem 5, \(\phi_\mathbf{v}(x)\) divides \(m(G,x)\) for any walk vector \(\mathbf{v}\). We thus apply Theorem 2 to obtain the following important result.
Theorem 8. For any walk vector \(\mathbf{v}\), \(\phi_\mathbf{v}(x)\) is a monic polynomial with integer coefficients.
Theorem 8 extends the result in [11], there proved only for \(\mathbf{v}=\mathbf{j}\), to any walk vector of any pseudo walk matrix with starting and ending vertices in any subset of \(\mathcal{V}^2\).
The following is a rather noteworthy corollary of Theorem 8.
Corollary 2. In the statement of Theorem 7, \(|\mathbf{N}|\) is an integer multiple of \(|\mathbf{H}|\) for any coefficient of \(\phi_\mathbf{v}(x)\).
Recall that we had split the set of distinct eigenvalues \(\Lambda\) into \(r\) mutually disjoint subsets \(\Lambda_1,\ldots,\Lambda_r\), where each subset \(\Lambda_i\) contains all the conjugates of some eigenvalue \(\lambda_i\). Because of Theorem 8, the set of \(\mathbf{v}\)-main eigenvalues of \(G\) must be the union of some or all of these \(\Lambda_i\) subsets.Theorem 9. If \(\lambda\in\Lambda_i\) is a \(\mathbf{v}\)-main eigenvalue of \(G\), then any other \(\lambda_k\) in \(\Lambda_i\) is also a \(\mathbf{v}\)-main eigenvalue of \(G\).
Proof. By Theorem 8, \(\phi_\mathbf{v}(x)\) is monic with integer coefficients. Let us write \(\phi_\mathbf{v}(x)\) as the product \(p_1(x)\ldots p_t(x)\) of all polynomial factors over \(\mathbb{Q}\), all of which must also be monic with integer coefficients thanks to Theorem 2. Since \(\lambda\) is a \(\mathbf{v}\)-main eigenvalue, its minimal polynomial \(\displaystyle\!\!\prod_{\lambda_k\in\Lambda_i}\!\!(x-\lambda_k)\) must be one of these \(p_j(x)\). This proves that all eigenvalues in \(\Lambda_i\) are \(\mathbf{v}\)-main.
By the Perron-Frobenius theorem for irreducible non-negative matrices, the largest eigenvalue \(\lambda_1\) of the adjacency matrix of any connected graph is simple and the components of its associated eigenvector are all positive [3, Theorem 1.3.6]. Thus, if the walk vector \(\mathbf{v}\) is a \(0\)-\(1\) vector corresponding to a walk matrix (rather than a pseudo walk matrix), then \(\lambda_1\) will necessarily be \(\mathbf{v}\)-main. It turns out that this is also true for walk vectors associated with pseudo walk matrices.
In order to prove this result, we first recall the main result of [1] in Theorem 10 below that explicitly obtains a walk vector \(\mathbf{v}\) for any subset \(S\) of \(\mathcal{V}^2\). Recall that what we mean by this is that \(\mathbf{v}\) can always be obtained from \(S\) so that the Gram matrix of the columns of \(\mathbf{W}_\mathbf{v}\) is a Hankel matrix with constant skew diagonals containing the walk enumerations \(w_0(S),\ldots,w_{2n-2}(S)\).
Theorem 10 ([1, Theorem 3.1]). Let \(S\) be any subset of \(\mathcal{V}^2\). Then \(\mathbf{v}\) is a walk vector associated with \(S\) if \(\mathbf{v}=\mathbf{X}\mathbf{d}\), where \(\mathbf{X}\) is an orthogonal matrix whose columns are \(n\) orthonormal eigenvectors of \(G\) associated with its \(n\) (possibly not distinct) eigenvalues and \(\mathbf{d}\) is any column vector where, for \(k=1,2,\ldots,n\), its \(k^{th}\) entry \(\left[\mathbf{d}\right]_k\) is \(\pm\sqrt{\sum_{(u,v)\in S}\left[\mathbf{X}\right]_{uk}\left[\mathbf{X}\right]_{vk}}\).
Theorem 11. \(\lambda_1\) is a \(\mathbf{v}\)-main eigenvalue for any walk vector \(\mathbf{v}\).
Proof. Let \(\mathbf{X}\) be as in the statement of Theorem 10. Without loss of generality, we assume that the first column of \(\mathbf{X}\) is \(\mathbf{x}_1\), the eigenvector associated with \(\lambda_1\). Then, by Theorem 10, \(\mathbf{v}^{T}\mathbf{x}_1=\mathbf{d}^{T}\mathbf{X}^{T}\mathbf{x}_1=\mathbf{d}^{T}\mathbf{e}_1=\left[\mathbf{d}\right]_1\). By the same theorem, this number is equal to \(\pm\sqrt{\sum_{(u,v)\in S}\left[\mathbf{X}\right]_{u1}\left[\mathbf{X}\right]_{v1}}\), or \(\pm\sqrt{\sum_{(u,v)\in S}\left[\mathbf{x}_1\right]_u\left[\mathbf{x}_1\right]_v}\). Since the entries of \(\mathbf{x}_1\) are all positive, this quantity is nonzero, as required.
Combining the results in this section, we reveal the following important theorem, upon which the remainder of this paper is based.
Theorem 12. The rank of \(\mathbf{W}_\mathbf{v}\), for any walk vector \(\mathbf{v}\), is equal to \(|\Lambda_1|+g_2|\Lambda_2|+g_3|\Lambda_3|+\cdots+g_r|\Lambda_r|\), where each of \(g_2,g_3,\ldots,g_r\) is either \(0\) or \(1\) (and these \(g_i\)'s may possibly be different for different walk vectors \(\mathbf{v}\)).
Theorem 12 limits the possible values for the rank of \(\mathbf{W}_\mathbf{v}\) quite significantly, especially if \(r\) is small. Indeed, if \(r=1\), we have the following interesting result.
Theorem 13. If \(\phi(G,x)\) is irreducible over \(\mathbb{Q}\), then \(\mathbf{W}_\mathbf{v}\) has rank \(n\) for all walk vectors \(\mathbf{v}\).
If \(r=2\), that is, if \(m(G,x)\) factors into just two monic polynomials over \(\mathbb{Q}\) (both with integer coefficients), then each pseudo walk matrix associated with \(G\) has just two possible values for its rank.
Theorem 14. Suppose \(m(G,x)=p_1(x)\,p_2(x)\) where both \(p_1(x)\) and \(p_2(x)\) are irreducible polynomials (over \(\mathbb{Q}\)) with integer coefficients. If \(p_1(x)\) is a polynomial of degree \(d\) having \(\lambda_1\) as a root, then for any walk vector \(\mathbf{v}\), the rank of \(\mathbf{W}_\mathbf{v}\) is either \(d\) or \(s\), the number of distinct eigenvalues of \(G\).
In Example 1, we mentioned that the cycle \(C_7\) has minimal polynomial \((x-2)(x^3+x^2-2x-1)\). By Theorem 14, we immediately infer that the rank of any pseudo walk matrix of \(C_7\) is either \(1\) or \(4\).
In the case of Example 1, the rank of \(\mathbf{W}_\mathbf{j}\) is clearly one, since \(C_7\) is a regular graph. The following result tells us that, indeed, such pseudo walk matrices of rank one only occur for regular graphs.
Theorem 15. If a graph \(G\) is not regular, then none of its pseudo walk matrices has rank one.
Proof. Suppose the pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) has rank one. Then \(\mathbf{A}\mathbf{v}=\mu\mathbf{v}\) where \(\mu\) is the largest eigenvalue of \(\mathbf{A}\), which must be an integer by Theorem 8. The number of walks \(w_0,w_1,w_2,w_3,\ldots\) of length \(0,1,2,3,\ldots\) within the set \(S\) for which \(\mathbf{v}\) is a walk vector are thus \(\mathbf{v}^{T}\mathbf{v},\mu(\mathbf{v}^{T}\mathbf{v}),\mu^2(\mathbf{v}^{T}\mathbf{v}),\mu^3(\mathbf{v}^{T}\mathbf{v}),\ldots\). In other words, \(w_k=\mu\,w_{k-1}\) for all walk lengths \(k\geq 1\). This is only possible if \(G\) is a regular graph of degree \(\mu\).
Since \(\mathbf{W}_\mathbf{j}\) is always a pseudo walk matrix of rank one for regular graphs, we have:
Corollary 3. A pseudo walk matrix associated with some subset \(S\) of \(\mathcal{V}^2\) of a graph \(G\) has rank one if and only if \(G\) is a regular graph.
In Section 8, we shall reveal more results on pseudo walk matrices of regular graphs.
Because of Theorem 12, we propose that rather than finding the set of eigenvalues of \(G\) to determine the rank of a (pseudo) walk matrix, we first perform a polynomial factorization of \(m(G,x)\) over \(\mathbb{Q}\). The number of such factors and their degrees sheds a very important light on the rank of any pseudo walk matrix. Indeed, in the case when such a factorization is not possible, the rank is immediately inferred to be \(n\).
5. Control theory
A graph is said to be controllable if \(\mathbf{W}_\mathbf{j}\) is invertible; equivalently, if all the eigenvalues of \(G\) are simple and (j)-main [4,5,12]. Other papers such as [7,8,13] additionally consider pairs \((\mathbf{A},\mathbf{b})\) for \(0\)-\(1\) vectors \(\mathbf{b}\). In the same way as for controllable graphs, such pairs are controllable if \(\mathbf{W}_\mathbf{b}\) is invertible, or, equivalently, if all eigenvalues of \(G\) are simple and \(\mathbf{b}\)-main.The terminology `controllable' arises from the following class of problems in control theory. Consider the following discrete system with state \(\mathbf{x}[k]\) at time \(k\) \((k=0,1,2,3,\ldots)\) satisfying the recurrence relation
The system governed by (8) is controllable if, given an initial state \(\mathbf{x}[0]\) and a future state \(\mathbf{s}\), there exists a time \(K\geq 0\) and an input \(u[k]\) such that \(\mathbf{x}[K]=\mathbf{s}\) [14, Definition 6.1]. The Kalman controllability criterion, a well-known criterion for system controllability, states that (8) is controllable if and only if the rank of the controllability matrix \(\begin{pmatrix}\mathbf{q} & \mathbf{M}\mathbf{q} & \mathbf{M}^2\mathbf{q} & \ldots & \mathbf{M}^{n-1}\mathbf{q}\end{pmatrix}\) is full. We immediately note that the controllability matrix is precisely the pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) whenever \(\mathbf{M}=\mathbf{A}\) and \(\mathbf{q}=\mathbf{v}\). This explains why we were so keen on obtaining the rank of \(\mathbf{W}_\mathbf{v}\), and why we say that, for a \(0\)-\(1\) vector \(\mathbf{b}\), the pair \((\mathbf{A},\mathbf{b})\) is controllable whenever the rank of \(\mathbf{W}_\mathbf{b}\) is full.
In the control theory literature, there is also the Popov-Belevitch-Hautus (PBH) test, another necessary and sufficient test for the controllability of (8). It says that the system is controllable whenever none of the eigenvectors of \(\mathbf{M}\) is orthogonal to \(\mathbf{q}\) [15, Theorem 6.2-5 (1.)]. This agrees with the more general results presented in Theorem 5 and Corollary 1 of this paper.
We shall henceforth consider the system
When \(\mathbf{v}\) is a \(0\)-\(1\) vector \(\mathbf{b}\), the input \(u[k]\) will affect the vertices in the set \(V\) indicated by \(\mathbf{b}\). As mentioned in Section 3, the formal power series produced from the expression \(\mathbf{b}^{T}(\mathbf{I}-x\mathbf{A})^{-1}\mathbf{b}\) is \(\sum_{k=0}^\infty (w_k(V\times V))x^k\). We may, however, rewrite the right hand side as \(\displaystyle\sum_{k=1}^s \dfrac{(\mathbf{b}^{T}\mathbf{x}_k)^2}{1-\lambda_kx}\), where, for all \(k\), \(\mathbf{x}_k\) is an appropriate\(^{2}\) choice of eigenvector associated with \(\lambda_k\). Clearly this function will have \(n\) distinct poles when \(n=s\) (that is, if all eigenvalues are distinct) and when no eigenvector \(\mathbf{x}_k\) is orthogonal to \(\mathbf{b}\). Hence the pair \((\mathbf{A},\mathbf{b})\) is controllable if and only if the rational function \(\mathbf{b}^{T}(\mathbf{I}-x\mathbf{A})^{-1}\mathbf{b}\) has \(n\) distinct poles [8, Lemma 2.1].
In the same way, we have defined a walk vector \(\mathbf{v}\) associated with any subset \(S\) of \(\mathcal{V}^2\) such that
\[\mathbf{v}^{T}(\mathbf{I}-x\mathbf{A})^{-1}\mathbf{v}=\sum_{k=0}^\infty (w_k(S))x^k=\sum_{k=1}^s \dfrac{(\mathbf{v}^{T}\mathbf{x}_k)^2}{1-\lambda_kx}.\] The system (9) where \(\mathbf{v}\) is a walk vector associated with \(S\) would have its input \(u[k]\) affecting all the pairs of vertices in \(S\).Thus, it is natural to extend the consideration of controllable pairs \((\mathbf{A},\mathbf{b})\) pertaining to pairs of vertices in a subset \(V\times V\) of \(\mathcal{V}^2\), where \(\mathbf{b}\) is an indicator vector of \(V\), to the more general consideration of controllable pairs \((\mathbf{A},\mathbf{v})\) pertaining to pairs of vertices in any subset \(S\) of \(\mathcal{V}^2\), where \(\mathbf{v}\) is the walk vector of \(S\). We thus define the pair \((\mathbf{A},\mathbf{v})\) to be controllable if all eigenvalues of \(G\) are simple and \(\mathbf{v}\)-main, or, equivalently, if the pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) is invertible.
6. Graphs with an irreducible characteristic polynomial
Theorem 13 tells us that graphs having an adjacency matrix with an irreducible characteristic polynomial are quite special.Theorem 16. If \(\phi(G,x)\) is irreducible over \(\mathbb{Q}\), then the pair \((\mathbf{A},\mathbf{v})\) is controllable for any walk vector \(\mathbf{v}\).
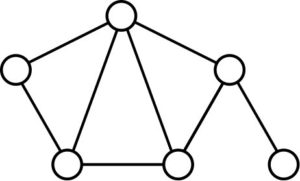
Theorem 16 above generalizes the result of [8, Theorem 5.3], which only mentions the walk vectors in the set \(\{\mathbf{j},\mathbf{e}_1,\ldots,\mathbf{e}_n\}\).It was proved in [16] that the ratio of controllable graphs on \(n\) vertices to all non-isomorphic graphs on \(n\) vertices tends to \(1\) as \(n\) increases. By Theorem 16, any graph with an irreducible characteristic polynomial over \(\mathbb{Q}\) is controllable. The converse is false; the smallest example of a controllable graph with a factorizable polynomial is that of Figure 1, having characteristic polynomial \(x(x^5-8x^3-6x^2+8x+6)\). Observe that, by Theorem 14, the rank of every pseudo walk matrix associated with this graph must be either \(5\) or \(6\).
Figure 1. The smallest controllable graph with a factorizable characteristic polynomial over \(\mathbb{Q}\).
Table 1. The number of connected graphs \(G(n)\), connected controllable graphs \(C(n)\) and connected graphs with an irreducible characteristic polynomial \(I(n)\) on \(n\) vertices.
| \(n\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(G(n)\) | 1 | 1 | 2 | 6 | 21 | 112 | 853 | 11117 | 261080 | 11716571 |
| \(C(n)\) | 1 | 0 | 0 | 0 | 0 | 8 | 85 | 2275 | 83034 | 5512362 |
| \(I(n)\) | 1 | 0 | 0 | 0 | 0 | 7 | 54 | 1943 | 62620 | 4697820 |
The characteristic polynomial of a disconnected graph is the product of the characteristic polynomials of each of its components. Thus, no disconnected graph has an irreducible characteristic polynomial, justifying the consideration of only connected graphs in Table 1.
We remark that roughly six out of every seven controllable graphs on up to ten vertices have an irreducible characteristic polynomial. This seems to suggest that the quantity \(\frac{I(n)}{G(n)}\), like \(\frac{C(n)}{G(n)}\), may also approach \(1\) as \(n\) tends to infinity. The empirical evidence warrants the formulation of the following conjecture.
Conjecture 1. \(\displaystyle\lim_{n\to\infty}\frac{I(n)}{G(n)}=1.\)
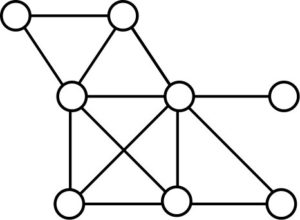
Among the 31 controllable graphs on seven vertices having a factorizable characteristic polynomial, 28 of them have zero as one of their eigenvalues [6]; indeed, each of their characteristic polynomial factorizes into \(x\) and some irreducible polynomial of degree six. The other three, depicted in Figure 2, factor into \((x+2)\) and an irreducible polynomial of degree six.Figure 2. The three controllable graphs on seven vertices whose characteristic polynomial factors into \((x+2)\) and an irreducible polynomial of degree six.
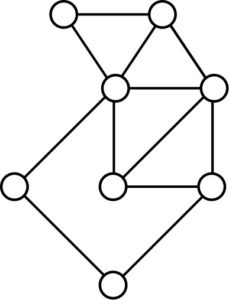
Figure 3. A controllable graph on eight vertices having characteristic polynomial \((x^4-x^3-9x^2-7x+1)(x^4+x^3-3x^2-x+1)\).
Figure 4. A controllable graph on eight vertices having characteristic polynomial \(x(x-1)(x+2)(x^5-x^4-9x^3-x^2+15x+7)\).
Conjecture 2. Let a graph \(G\) have adjacency matrix \(\mathbf{A}\). The pair \((\mathbf{A},\mathbf{v})\) is controllable for any walk vector \(\mathbf{v}\) if and only if \(\phi(G,x)\) is irreducible over \(\mathbb{Q}\).
7. Results on controllable pairs
Let \(\mathbf{b}_1\) and \(\mathbf{b}_2\) be any two \(0\)-\(1\) vectors. The walk matrix \(\mathbf{W}_{\mathbf{b}_1}\) contains walk enumerations of walks starting and ending within the subset \(V_1\) of \(\mathcal{V}(G)\) such that \(\mathbf{b}_1\) is the indicator vector of \(V_1\); we can say a similar statement for \(\mathbf{W}_{\mathbf{b}_2}\). Moreover, similarly to (3),However, by Theorem 10, there exists a walk vector \(\mathbf{v}\) associated with \(V_1\times V_2\) such that the Gram matrix of the columns of the pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) is equal to the matrix in (10). Moreover, this Gram matrix must have the same rank as \(\mathbf{W}_\mathbf{v}\). Thus, we have the following lemma.
Lemma 2. The rank of the pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) associated with the subset \(V_1\times V_2\) of \(\mathcal{V}^2\) is equal to the rank of \({\mathbf{W}_{\mathbf{b}_1}}^{T}\mathbf{W}_{\mathbf{b}_2}\), where \(\mathbf{b}_1\) and \(\mathbf{b}_2\) are the \(0\)-\(1\) indicator vectors of \(V_1\) and \(V_2\) respectively.
Clearly if both \({\mathbf{W}_{\mathbf{b}_1}}\) and \(\mathbf{W}_{\mathbf{b}_2}\) are invertible, then so is \({\mathbf{W}_{\mathbf{b}_1}}^{T}\mathbf{W}_{\mathbf{b}_2}\). Thus we have the following result.Theorem 17. Let \(\mathbf{b}_1\) and \(\mathbf{b}_2\) be indicator vectors of two subsets \(V_1\) and \(V_2\) of \(\mathcal{V}(G)\). Moreover, let \(\mathbf{v}\) be the walk vector of \(V_1\times V_2\). If \((\mathbf{A},\mathbf{b}_1)\) and \((\mathbf{A},\mathbf{b}_2)\) are both controllable pairs, then so is the pair \((\mathbf{A},\mathbf{v})\).
A graph is omnicontrollable if \((\mathbf{A},\mathbf{e}_i)\) is a controllable pair for all \(i\in\{1,2,\ldots,n\}\) [7,13]. Because of Theorem 17, omnicontrollable graphs have many more controllable pairs apart from \((\mathbf{A},\mathbf{e}_1),\ldots,(\mathbf{A},\mathbf{e}_n)\).Corollary 4. Let \(\mathbf{v}_{(i,j)}\) be a walk vector associated with the set containing the single pair \(\{(i,j)\}\) whose Gram matrix of the columns of its pseudo walk matrix counts walks starting from vertex \(i\) and ending at vertex \(j\) in an omnicontrollable graph \(G\). The pair \((\mathbf{A},\mathbf{v}_{(i,j)})\) is controllable for any two vertices \(i\) and \(j\) in \(G\).
Proof. When \(i=j\), the result is immediate by definition of an omnicontrollable graph. Thus suppose \(i\ne j\). Then \((\mathbf{A},\mathbf{e}_i)\) and \((\mathbf{A},\mathbf{e}_j)\) are controllable pairs for any \(i\) and \(j\). Since \(\{i\}\times\{j\}=\{(i,j)\}\), the result follows by applying Theorem 17.
8. Recalcitrant pairs
If a pair \((\mathbf{A},\mathbf{v})\) is not controllable, then the pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) would not have full rank. For instance, graphs having at least one repeating eigenvalue can have no controllable pair \((\mathbf{A},\mathbf{v})\) for any walk vector \(\mathbf{v}\); this is a consequence of Theorem 6. Indeed, by using Theorem 1, we can present the following result.Theorem 18. If \(\phi(G,x)\) and \(\phi^\prime(G,x)\) have some polynomial common factor, then no walk vector \(\mathbf{v}\) exists such that the pair \((\mathbf{A},\mathbf{v})\) is controllable.
By Theorem 12, the rank of any pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) is at least \(|\Lambda_1|\), the degree of the minimal polynomial of the largest eigenvalue \(\lambda_1\). As already mentioned in Section 6, if \(|\Lambda_1|=n\), then \(\phi(G,x)\) would be irreducible and all pairs \((\mathbf{A},\mathbf{v})\) would be controllable. Thus we assume that \(|\Lambda_1|< n\) in this section.We introduce the following terminology for when the rank of \(\mathbf{W}_\mathbf{v}\) attains this lower bound \(|\Lambda_1|\):
Definition 19. For a graph with adjacency matrix \(\mathbf{A}\) that does not have an irreducible characteristic polynomial, the pair \((\mathbf{A},\mathbf{v})\) is called recalcitrant if the rank of the pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) associated with the walk vector \(\mathbf{v}\) is equal to the degree of the minimal polynomial of the largest eigenvalue of \(\mathbf{A}\).
We make use once again of Lemma 2. It is well-known (see, for example, [9, Section 0.4.5(c)]) that the rank of the product of two matrices is at most equal to the rank of the one having the smaller rank. This means that if, in Lemma 2, one of \(\mathbf{W}_{\mathbf{b}_1}\) or \(\mathbf{W}_{\mathbf{b}_2}\) has the smallest rank possible, then so will the rank of \({\mathbf{W}_{\mathbf{b}_1}}^{T}\mathbf{W}_{\mathbf{b}_2}\).Theorem 20. Let \(\mathbf{b}_1\) and \(\mathbf{b}_2\) be indicator vectors of two subsets \(V_1\) and \(V_2\) of \(\mathcal{V}(G)\). Moreover, let \(\mathbf{v}\) be the walk vector of \(V_1\times V_2\). If one of \((\mathbf{A},\mathbf{b}_1)\) or \((\mathbf{A},\mathbf{b}_2)\) (or both) is a recalcitrant pair, then the pair \((\mathbf{A},\mathbf{v})\) is also recalcitrant.
Note that if a graph has \(n\) distinct eigenvalues and its characteristic polynomial factors into exactly two monic polynomials with integer coefficients, then \((\mathbf{A},\mathbf{v})\) is either controllable or recalcitrant for all walk vectors \(\mathbf{v}\). Thus, for such graphs, if the rank of all walk matrices (that is, those having a walk vector with \(0\)-\(1\) entries) is known, then the rank of the pseudo walk matrices whose walk vectors are associated with a subset of \(\mathcal{V}^2\) of the form \(V_1\times V_2\) (\(V_1,V_2\subseteq\mathcal{V}(G)\)) may be inferred by simply applying Theorem 17 or Theorem 20.We can apply Theorem 20 to regular graphs.
Corollary 5. If \(G\) is a regular graph, then the pair \((\mathbf{A},\mathbf{v})\) is recalcitrant for any walk vector \(\mathbf{v}\) associated with the set \(V\times\mathcal{V}(G)\) for all \(V\subseteq\mathcal{V}(G)\). Moreover, the pseudo walk matrices of all such walk vectors have rank one.
Proof. The rank of the walk matrix \(\mathbf{W}_\mathbf{j}\) associated with a regular graph \(G\) is one; indeed, \(\mathbf{A}\mathbf{j}=\Delta\mathbf{j}\) where \(\Delta\) is the common degree (and the largest eigenvalue) of \(G\). Hence \((\mathbf{A},\mathbf{j})\) is a recalcitrant pair. By Theorem 20, any walk vector \(\mathbf{v}\) associated with \(V\times\mathcal{V}(G)\), where \(V\) is any subset of \(\mathcal{V}(G)\), must also be recalcitrant. Moreover, any such pseudo walk matrices \(\mathbf{W}_\mathbf{v}\) must have the same rank as that of \(\mathbf{W}_\mathbf{j}\), that is, rank one.
From the proof of Corollary 5, we remark that a pseudo walk matrix \(\mathbf{W}_\mathbf{v}\) has rank one if and only if \(\mathbf{v}\) is an eigenvector associated with the (integer) eigenvalue \(\lambda_1\) of \(\mathbf{A}\). Because of this, for a connected regular graph, the pseudo walk matrices of rank one must have walk vectors \(\mathbf{v}\) of the form \(\sqrt{\frac{m}{n}}\mathbf{j}\) for some integer \(m\) between \(1\) and \(n\), so that \(\mathbf{v}^{T}\mathbf{v}\), or \(w_0(S)\), would be an integer between \(1\) and \(n\).
Since non-regular graphs cannot have pseudo walk matrices of rank one by Theorem 15, we have the following corollary by combining this theorem with Corollary 5.
Corollary 6. If a non-regular graph has its largest eigenvalue equal to an integer, then \((\mathbf{A},\mathbf{v})\) is not recalcitrant for any pseudo walk vector \(\mathbf{v}\).
The smallest example of a graph having the properties described in Corollary 6 is the star \(K_{1,4}\) on five vertices, whose characteristic polynomial is \(x^3(x-2)(x+2)\). Using Corollary 6 and Theorem 12, we can infer that the rank of any pseudo walk matrix for \(K_{1,4}\) must be either two or three. Thus, in the case of \(K_{1,4}\), any pair \((\mathbf{A},\mathbf{v})\) for any walk vector \(\mathbf{v}\) is neither controllable nor recalcitrant.Conflict of interests
The author declares no conflict of interest.References
- Farrugia, A. (2019). On Pseudo Walk Matrices. Discrete Mathematics Letters, 1, 8-15. [Google Scholor]
- Atiyah, M.F., & Macdonald, I.G. (1969). Introduction to Commutative Algebra. Westview Press. [Google Scholor]
- Cvetkovic, D., Rowlinson, P., & Simic, S.K. (2009). An Introduction to the Theory of Graph Spectra. Cambridge University Press. [Google Scholor]
- Cvetkovic, D., Rowlinson, P., Stanic, Z., & Yoon, M.G. (2011). Controllable Graphs. Bulletin Classe des Sciences Mathematiques et Naturelles, 143(36), 81-88. [Google Scholor]
- Cvetkovic, D., Rowlinson, P., Stanic, Z., & Yoon, M.G. (2011). Controllable graphs with least eigenvalue at least \(-2\). Applicable Analysis and Discrete Mathematics, 5(2), 165-175. [Google Scholor]
- Farrugia, A. (2016). On Strongly Asymmetric and Controllable Primitive Graphs. Discrete Applied Mathematics, 211, 58-67. [Google Scholor]
- Farrugia, A., Koledin, T., & Stanic, Z. (2020). Controllability of NEPSes of Graphs. Linear and Multilinear Algebra, 10.1080/03081087.2020.1778622. [Google Scholor]
- Godsil, C. (2012). Controllable Subsets in Graphs. Annals of Combinatorics, 16(4), 733-744.[Google Scholor]
- Horn, R.A., & Johnson, C.R. (2013). Matrix Analysis. Cambridge University Press, Second Edition. [Google Scholor]
- Powers, D.L., & Sulaiman, M.M. (1982). The Walk Partition and Colorations of a Graph. Linear Algebra and its Applications, 48, 145-159.[Google Scholor]
- Rowlinson, P. (2007). The Main Eigenvalues of a Graph: a survey. Applicable Analysis and Discrete Mathematics, 1, 445-471. [Google Scholor]
- Farrugia, A., & Sciriha, I. (2015). On the main eigenvalues of universal adjacency matrices and U-controllable graphs. Electronic Journal of Linear Algebra, 30, 812-826. [Google Scholor]
- Farrugia, A., & Sciriha, I. (2014). Controllability of undirected graphs. Linear Algebra and its Applications, 454, 138-157. [Google Scholor]
- Chen, Ch.Ts. (1998). Linear System Theory and Design. Oxford University Press, Inc., New York, NY, USA. [Google Scholor]
- Kailath, T. (1980). Linear Systems. Prentice-Hall Inc., Englewood Cliffs, N.J. [Google Scholor]
- O'Rourke, S., & Touri, B. (2016). On a conjecture of Godsil concerning controllable random graphs. SIAM Journal on Control and Optimization, 54(6), 3347-3378.[Google Scholor]
- Sloane, N.J.A. The On-Line Encyclopedia of Integer Sequences; Number of connected graphs with n nodes. Retrieved from https://oeis.org/A001349. [29 July 2020][Google Scholor]
- McKay, B.D. (1998). Isomorph-free exhaustive generation. Journal of Algorithms, 26, 306-324.[Google Scholor]