The evolutionary spatial snowdrift game on a cycle: An asymptotic analysis

1. Introduction

The snowdrift game (also known as the hawk-dove game) is attributed to Maynard Smith [1]. This game may be described as a contest between two motorists stuck in a snowdrift. Each individual may choose to exit her or his vehicle and shovel snow (cooperate) or a remain warm inside their car (defect). Assuming that being able to continue home is valued above having to shovel snow, the outcomes of the game are: Two cooperating individuals each shovel half the snow and continue on their way home, and so obtain the reward for mutual cooperation \(R\). A cooperating individual facing a defecting individual shovels all of the snow (but still gets to continue at least) and so obtains the sucker's payoff \(S\), while the defecting individual shovels no snow and may continue on her or his way; the temptation to defect \(T\). Finally, two defecting individuals stay put in their vehicles but cannot continue on their way home, and thus receive the punishment for mutual defection \(P\). These payoffs satisfy the inequality chain

The evolution of cooperation in the context of a competitive environment has been studied in the fields of evolutionary dynamics, economics, ecology and game theory for many years. In 1984, Axelrod [2] hosted two computer tournaments in which game theorists and enthusiasts could submit strategy schemes which were to compete against one another in the setting of the iterated prisoner's dilemma. The prisoner's dilemma is a 2-person, 2-strategy game with the same strategies as those described above, but with payoffs satisfying the inequality chain \(T>R>P>S\). The results of the tournaments were analysed by Axelrod in the hope of identifying characteristics of successful strategies. He found that "nice" strategies (strategies which do not defect unless provoked) outperform strictly competitive strategies. This has since led to a large body of work aimed at determining, within a variety of biological or economic systems, what gives rise to the evolution of cooperation. Other noteworthy work in the field of evolutionary game theory is concerned with the notion of an evolutionary stable strategy, introduced by Maynard Smith and Price [3]. Such a strategy is robust against invasion of other strategies in the context of an entire population playing it. For an overview of work in evolutionary game theory the interested reader may consult [4,5].

Introducing game theory into the realm of temporal evolutionary dynamics provided a mechanism for modelling a population of individuals competing with one another for opportunities to replicate themselves as offspring. Traditionally, their chance of replicating their genetic material into future generations depends on their fitness. Depending on the nature of the selection dynamics, their fitness is either slightly or largely influenced by their relative performance in the game. Strong selection refers to the situation in which an individual's fitness is mainly determined by its performance in the game while weak selection assigns individuals a standard fitness that is slightly perturbed based on the individual's performance in the game. Furthermore, the selection dynamics may be global in the sense that all individuals compete during every game round or local, in which case a specific individual is selected for replication according to a probability proportional to its fitness.

A spatial extension to evolutionary games was pioneered by Nowak and May [6] who argued that in natural settings players do not frequently interact with all other members of the population, but rather experience frequent local interactions with a few individuals. They therefore positioned players at the vertices of a grid graph allowing for local interaction with their neighbours only. A game round consisted of each player playing the game against each of its neighbours (in pairs) and updating its strategy in order to "copy" the strategy of its best performing neighbour. The game was simulated from various initial conditions until steady states were reached and the results showed that in the prisoner's dilemma, a spatial extension is beneficial to the evolution of cooperation as it allows for clusters of cooperation to withstand the pressure of surrounding defectors.

Spatial extensions to the snowdrift game have, however, yielded mixed results, in some cases aiding and in others hindering the evolution of cooperation [7,8]. Roca et al., [8] discussed the considerable dependence of this facilitation and hindrance of cooperation on the clustering of the spatial structure as well as the relevant strategy update rule. This indicates that further investigations into the nature of the spatial snowdrift game might be of interest in a variety of settings. In this paper we adopt an analytic approach towards studying the long-term strategy behaviour of players in a deterministic version of the evolutionary spatial snowdrift game (ESSG), arranged along a cycle. More specifically, we determine the probability of retaining some form of cooperation over game rounds and also establish bounds on the probability that a small number of players of a particular mutant strategy introduced randomly into a cycle of players who adopt the opposite strategy leads to a situation where all players eventually adopt the mutant strategy.

The remainder of this paper is organised as follows: Pertinent related literature is highlighted in §2. In §3, the dynamics of the game investigated are presented along with nomenclature pertaining to the representation of the game. We present the body of our investigation in §4, §5, and §6, each in the context of one of three regions of interest in the parameter phase plane of the game. Finally, a number of conclusions are presented in §7.

2. Related literature

Academic interest in games played on cycle graphs has varied over time, starting with the paper by Eshel et al., [9], in which a version of the prisoner's dilemma, which carefully selected parameter values was considered, allowing for a representation of the payoffs parameterised by only one parameter, namely \(C\), as \(T=1+C/2\), \(R=1\), \(P=C/2\), and \(S=0\), with the restriction that \(0< C< 1/2\). The update rule employed resulted in an individual adopting the strategy which yielded the largest average payoff to players in their closed neighbourhoods. The analysis included a characterisation of states that lead to persistent cooperation, as well as an implicit calculation of the probability of persistent cooperation in the limit as the population grows large. Moreover, the existence of groups of defectors was established which alternate between having length \(d=1\) and length \(d=3\). They also analysed mutation dynamics according to which each player mutates (switches its strategy) with constant probability \(\lambda\). The deterministic update model was morphed into a probabilistic model analysed using methods from the realm of Markov processes. The results showed that pockets of cooperators can grow amidst a sea of defectors while the reverse is not true.

There has since been recent interest in evolutionary games played on cycle graphs [10,11,12]. These graphs may be considered one-dimensional lattice structures and therefore represent a simplification of larger grid structures, allowing for analytical investigations instead of analyses based on simulation studies. The objective in such investigations is to gain insight into the intrinsic nature of potential strategy interactions in more general graph structures.

The first of these investigations was carried out by Ohtsuki and Nowak [10] and pertained to 2-person, 2-strategy games played on cycle graphs in the context of three different update rules, namely birth-death, death-birth, and imitation. According to all three rules, a singular player is selected randomly during each game round whose strategy is to be updated. The investigation of Ohtsuki and Nowak related to the notion of fixation probabilities. A fixation probability is the probability of a player playing strategy \(A\), introduced into a population of players all playing strategy \(B\), resulting in the entire population adopting strategy \(A\) during a future generation.

Burger et al., [11] studied an evolutionary version of the prisoner's dilemma on a cycle in which the payoffs were normalised to \(T>1>P>0\), having set \(R=1\) and \(S=0\). The update rule was deterministic and synchronous in nature, meaning that each player would update its strategy during every round to the strategy of the best-performing player in its closed neighbourhood, and keeping it unaltered in the case of a tie between two strategies. One of the main results of the investigation was a quantification of the probability of achieving persistent cooperation ( i.e.the strategy of cooperation occurring in a steady state of the game) from a random initial assignment of strategies to the players on the cycle. While pockets of adjacent cooperation could not grow in this game, as the payoff of a cooperator adjacent to a defector would never exceed that of the defectors, it was shown that the aforementioned probability of persistent cooperation nevertheless tends to unity as the order of the cycle increases. Initial states of the game that lead to a steady state containing cooperation were also characterised. As found in [6], structures that lead to persistent cooperation involve clusters of cooperators surrounded by clusters of defectors. The reason for this finding is that interior cooperators may achieve a larger payoff than that of the first defector adjacent to the cluster of cooperators and so the cooperators on the boundaries of same-strategy clusters retain their strategies. The steady states of the game were also enumerated in terms of the order of the underlying cycle.

Finally, Laird [12] conducted an investigation into standoffs between cooperators and defectors in the ESSG. These standoff structures are only attainable when the payoff obtained by cooperators and defectors can be equal, leading to a situation where ties can occur on the boundaries between clusters of cooperators and clusters of defectors. The game under investigation was, however, semi-stochastic in the sense that a single player is chosen during each round and its payoff is compared with the payoffs obtained by its neighbours, upon which the player probabilistically changes its strategy to that of one of its neighbours strategies if these achieve larger payoffs than its own. This game dynamic allows for various game rounds during which no changes occur in the distribution of player strategies, even if adjacent players' payoffs are indeed distinct at the boundary between two clusters of differing strategies. Standoffs were found to occur for payoff parameters for which the equalities \(T=2S\) and \(T=S+1\) hold, upon normalisation so that \(P=0\) and \(R=1\).

3. Problem and nomenclature

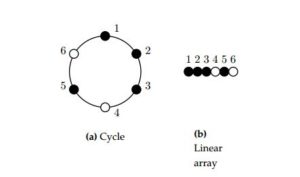
The game considered in this paper is the (deterministic) ESSG, with players arranged along a cycle of order \(n\) and with payoff parameters normalised as described in the previous section so that \(T>1>S>0\). A game state is an allocation of strategies to the players in the population during any game round. Such a game state is represented succinctly by a binary string \(W\) of characters \(W_1W_2\cdots W_n\) in which \(W_x\in \{C,D\}\) for each \(x\in\{1,2,\ldots,n\}\), depending on the strategy (cooperation, denoted by \(C\), or defection, denoted by \(D\)) of player \(x\). The players are numbered so that player \(x\) is adjacent to players \(x\pm 1\text{ (mod }n)\), forming the underlying population structure of a cycle. A run is a maximal (contiguous) substring of \(W\) representing players playing the same strategy. A game state may be represented graphically by a two-colouring of the vertices of the underlying cycle graph in which the two colours represent the two strategies. This representation may be abbreviated by representing the player strategies in the form of a linear array of coloured vertices, with wrapping of is extremal vertices. Consider, as an example, the state \(CCCDCD\) of the ESSG on a cycle of order 6 depicted graphically in Figure 1. The convention adopted in the graphical representation is that a solid vertex represents a player playing the strategy of cooperation, while an open vertex represents a player playing the strategy of defection.

An automorphism is a mapping \(f: W^1 \mapsto W^2\) from one game state \(W^1\) to another state \(W^2\) (called automorphic states) in which adjacency of players as well as strategy allocation is preserved (i.e. players \(x\) and \(y\) playing strategies \(W_x^1\) and \(W_y^1\), respectively, in \(W^1\) are adjacent in the cycle if and only if players \(f(x)\) and \(f(y)\) play the strategies \(W_{f(x)}^2\) and \(W_{f(y)}^2\), respectively, in \(W_2\)). An automorphism class is a maximal subset of game states that are pairwise automorphic. An (automorphism) class leader is the lexicographically smallest member \(W\) of the particular automorphism class, taking \(C< D\) in the string \(W\). For the special case where \(n=5\), for example, the automorphism classes and their leaders are shown in Table 1.

During every round of the ESSG on a cycle, each player plays the snowdrift game, adopting its chosen strategy, against both of its neighbours in the underlying cycle and sums the payoffs thus obtained. Each player then compares its own total payoff with those of its two neighbours, adopting the strategy of the best-performing neighbour during the following round. The game dynamics are succinctly summarised in the form of a state graph, as defined in [13]. The state graph of the ESSG is a directed graph in which each vertex represents a game state, and in which a directed edge of the form \((W^1, W^2)\) indicates that the state \(W^1\) transitions to the state \(W^2\) during a single round of the game. Only automorphism class leaders appear in the state graph, however, each representing its entire class. Since the ESSG is deterministic, each vertex of its state graph has an outdegree of 1 (possibly forming a loop).

Because the state graph of the ESSG on a cycle of order \(n\) is finite (its order is at most \(2^n\)), the (infinite) sequence \(W^{1}, W^{2}, W^{3},\ldots\) of states in any ESSG instance necessarily ends in an infinite tail of repetition in one of two fundamentally different forms. The first is a limit cycle, which is represented by a directed cycle of length at least \(2\) in the state graph of the ESS. Note, therefore, that the states in a limit cycle are pairwise non-automorphic. The other fundamental form of repetition in which the sequence of game states can end is represented by a loop (a directed cycle of length \(1\)) in the state graph. A distinction is made between two different incarnations of the latter form of repetition. The first incarnation occurs if a game state \(W^{*}\) is reached during some round \(t^*\) upon which the state of the game during round \(t\) remains equal to \(W^*\) for all \(t\geq t^*\). In this case, the game state \(W^*\) is called a steady state. The second incarnation occurs if a game state \(W\) is reached (for the first time) during some round \(t\) upon which the state of the game during round \(t\) is automorphic (but not necessarily identically equal) to \(W\) for all \(t>t\). In this case, the game state \(W\) and all its subsequent states are collectively called a set of transient states. The union of the set of all steady states, the collection of all states appearing in sets of transient states and the set of all states appearing in limit cycles is referred to as the set of end states. Every component of the state graph of the ESSG therefore contains at least one end state.

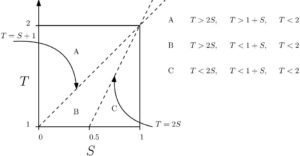
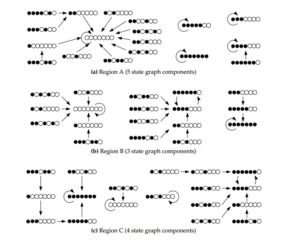
Our objective in this paper is to elucidate the nature of end states of the ESSG and to characterise game states that lead asymptotically to end states containing the strategy of cooperation, referred to as the situation of persistent cooperation (i.e. game states from which the strategy of cooperation is not completely eradicated). The asymptotic game behaviour, however, depends fundamentally on the relationship between the payoff parameters \(S\) and \(T\) employed in the game. The isoclines in the \((S,T)\)-phase plane, indicated as dotted lines in Figure 2, are obtained by setting the payoffs obtainable by players adjacent to the boundaries between runs of different strategies in a game state equal to one another, i.e. \(T=S+1\) and \(T=2S\). The payoff \(2T\) received by a defector playing against two cooperators is not considered for isocline purposes as this is by definition the largest payoff attainable and should always win. The opposite is true for the payoff 0, obtained by a defector playing against two defectors. As a result, the phase plane consists of three regions (denoted by A, B and C) in which differing game dynamics are anticipated. This anticipation is confirmed by the state graphs of the ESSG on a cycle of order 7 for Regions A, B and C of the \((S,T)\)-phase plane, shown in Figure 3. The remainder of the material in this paper is partitioned into sections according to the three phase plane regions.

4. Game analysis in Region A

In Region A of the \((S,T)\)-phase plane in Figure 2, the payoffs of players adhere to the inequality chain \(0< 2S< S+1< T< 2< 2T\). In this region, the only payoffs obtainable by cooperators that beat payoffs of defectors, are \(S+1>2S>0\), which is better than the payoff of a defector adjacent to two defectors, and \(2>T\) obtained by a cooperator adjacent to two cooperators. A cooperator adjacent to a defector receives a smaller payoff than the defector because the smallest payoff of a defector adjacent to a cooperator is \(T\), while the largest payoff of a cooperator adjacent to a defector is \(S+1\). This means that there can be no growth in length of a cooperation run from one state of the ESSG in Region A to the next. There may, however, be stationary cooperation runs that allow for cooperators to coexist together with defectors indefinitely.

Note that the point in Region A where \(S=0\) lies on the boundary of the region and only violates the inequality \(2S>0\), which is a comparison of the payoffs of a defector adjacent to two defectors and of a cooperator adjacent to two defectors. Such a comparison is only realised in the partial state \(DDDCD\) and the violated inequality plays no role as the third defector obtains a payoff of \(T\) while the cooperator obtains a payoff of \(2S< T\). All defectors therefore retain their strategy and the cooperator adopts the strategy of defection during the following round of the game.

Moreover, the study of the evolutionary spatial prisoner’s dilemma on a cycle in [11] is applicable to the ESSG in Region A. That study took place in a region of a \((P,T)\)-phase plane in which \(T+P\leq 2\), with \(1< T< 2\) and \(0< P< 1\), and so setting \(P=0\) would not alter their game either as the only requirement for the region in question was that \(T+P< 2\), which still holds if \(P=0\). The dynamics of the two games are equivalent in the regions cited because their update rules are identical and their payoff matrices can both be reduced to the form

The results of [11] therefore also hold for Region A of the ESSG on a cycle. For the sake of completeness, the characterisation of steady states, and the probability of persistent cooperation resulting from a randomly generated initial game state are recounted from Burger et al., [11] in the remainder of this section. Bounds on the previously unstudied notion of a fixation probability in the context of the ESSG on a cycle are finally established.

4.1. The probability of persistent cooperation in Region A

The following characterisation of game states that lead to some form of persistent cooperation is due to Burger et al., [11].

Theorem 1(Requirements for persistent cooperation, restated from [11]). In the ESSG on a cycle of order \(n\geq 5\) with the payoff values satisfying \(2S< S+1< T< 2\), a game state leads to persistent cooperation if and only if it contains at least one of the substates \(CCCCC\), \(DDCCCDD\), or \(DDCCCCD\).

Burger et al., [11] used the result of Theorem 1 to establish the probability of persistent cooperation resulting from a randomly generated game state, as follows.

Theorem 2 (Probability of persistent cooperation, restated from [11]). In the ESSG on a cycle of order \(n\) with payoff parameters \(S\) and \(T\), satisfying \(2S< S+1< T\), the probability that a random distribution of strategies will lead to persistent cooperation is given by

where the value of \(a_n\) is defined by the recurrence relation with seed values \(a_{1}^{*}=1\), \(a_{2}^{*}=3\), \(a_{3}^{*}=7\), \(a_{4}^{*}=15\), \(a_5^{*}=26\), \(a_{6}^{*}=45\), and \(a_{7}^{*}=99\).

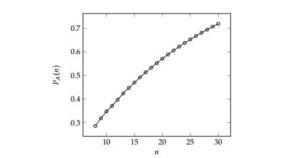
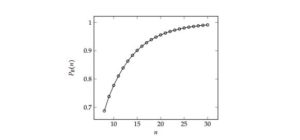
The values of \(a_n\) and \(2^n\) are tabulated in Table 2 for \(n\in \{8,\ldots,16\}\) and the probability of persistent cooperation \(P_A(n)\) is illustrated graphically in Figure 4 for \(n\in\{8,\ldots,30\}\).

Table 1.Values of \(a_n\) in (4) and \(2^n\) for \(n\in\{8,\ldots,16\}\) used to compute the probability \(P_A(n)=1-a_n / 2^n\) of persistent cooperation resulting from a randomly generated initial game state for the ESSG on a cycle of order \(n\), with payoff parameter values satisfying \(2S< S+1< T\).

\(n\)	8	9	10	11	12	13	14	15	16
\(a_n\)	183	349	668	1288	2469	4720	9061	17372	33303
\(2^n\)	256	512	1024	2048	4096	8192	16348	32768	65536

Closer inspection of the sequence \((a_n)_{n=8,9,10,\ldots}\) and the recurrence relation which defines it, as well as a comparison thereof with the sequence \((2^n)_{n=8,9,10,\ldots}\) yields the final result recounted in this section --- the limit of the probability of persistent cooperation as the order of the underlying cycle grows.

Theorem 3 (Limiting probability of persistent cooperation, restated from [11]). In the ESSG on a cycle of order \(n\) with payoff parameters \(S\) and \(T\), satisfying \(2S< S+1< T\), the probability \(P_A(n)\) of persistent cooperation satisfies \(\lim_{n\to\infty} P_A(n) = 1\).

Although the extent of a cooperation run cannot grow in Region A of the \((S,T)\)-phase plane, the strategy of cooperation would seem to be somewhat resilient in view of the above result.

4.2. Fixation probabilities in Region A

The traditional notion of a fixation probability in the deterministic setting of the ESSG on a cycle, as considered in this paper, is augmented by the requirements of both establishment and growth of the mutant strategy. A subpopulation of mutant cooperators can never fix an entire population of defectors because of the growth requirement (recall that there are no instances in which a defector adopts the strategy of cooperation in parameter Region A). This fact is formalised in the following observation.

Observation 1 (Fixation probability of the strategy of cooperation). In the ESSG on a cycle of order \(n\) with payoff parameters \(S\) and \(T\), satisfying \(2S < S+1< T\), the fixation probability \(F_A^C(n,k)\) of a subpopulation of \(k\) mutant cooperators among a population of \(n-k\) defectors is zero.

A lower bound on the fixation probability of a subpopulation of mutant defectors is established in the next observation.

Observation 2 (Fixation probability of the strategy of defection). In the ESSG on a cycle of order \(n\) with payoff parameters \(S\) and \(T\), satisfying \(2S < S+1< T\), the fixation probability \(F_A^D(n,k)\) of a subpopulation of \(k\) mutant defectors among a population of \(n-k\) cooperators satisfies

Proof. Recall that once a player has adopted the strategy of defection it will not return to the strategy of cooperation during any subsequent game round. This shows that a subpopulation of mutant defectors will certainly establish itself.

Consider the likelihood that the mutating defectors are distributed in such a manner that there are no defection runs of length at least 2 during the round in which the mutation occurs. This means that each mutant defector is a singleton and so all cooperators adjacent to mutants adopt the strategy of defection during the following game round because of the defectors' payoff value of \(2T\) each, the highest obtainable in the game. After the initial mutation, at least \(k\) cooperators will therefore adopt the strategy of defection during the following round in such a scenario (each initially mutated defector is adjacent to two possibly overlapping cooperators). The number of ways in which the \(k\) mutant defectors may be positioned as described above is \({n-k \choose k}\). The total number of arrangements of the \(k\) mutants among the \(n-k\) cooperating players is \({n-k+k-1\choose k}={n-1 \choose k}\). The probability of the scenario described above is therefore \({{n-k \choose k}}/{{n-1 \choose k}}\). This is, however, only a lower bound on the fixation probability of defection because in truth there only needs to be one such singleton defector for growth of the mutant strategy to occur.

The results of Observations 1 and 2 demonstrate that the strategy of defection is favoured above the strategy of cooperation in the ESSG on cycle in Region A. This claim would seem intuitive as there is never any growth in length of cooperation runs while defection runs are able to exhibit growth in some instances. It remains true that the probability of persistent cooperation in the ESSG on a cycle in Region A of the \((S,T)\)-phase plane is high and therefore cooperation is rarely eradicated entirely on large cycles, indicating that population structure is an enabler of cooperation.

5. Game analysis in Region B

In Region B of the \((S,T)\)-phase plane in Figure 2, the payoffs of players satisfy the inequality chain \(0< 2S< T< S+1< 2< 2T\). In this region, a cooperator playing against a defector receives a larger payoff than the defector if and only if it is also adjacent to a cooperator and the defector in question is adjacent to another defector (CCDD) because of the inequality \(S+1>T\). If the cooperator were instead adjacent to another defector (DCDD), its payoff of \(2S< T\) would not be sufficient to retain its strategy of cooperation, and if the defector were instead adjacent to another cooperator instead of a defector (CCDC), its payoff of \(2T>S+1\) would be the largest achievable. If each cooperation run and each defection run has length at least 2, the growth in length of each cooperation run will continue as long as the defection runs each has length at least 2.

5.1. Characterisation of game states leading to persistent cooperation

In this section, we characterise game states that lead to end states in Region B of the \((S,T)\)-phase plane containing the strategy of cooperation. By definition, steady states are end states in which no player updates its strategy from one round to the next and therefore the game remains in the same automorphism class indefinitely. There are, of course, two trivial steady states, the all-defector state and the all-cooperator state, in which no player updates its strategy as there is no opportunity for ''learning.'' This observation, in fact, also holds for players in the interior of any run of cooperation or defection.

Two other types of steady states may potentially exist, ones arising from ties between adjacent players of opposite strategies, and ones arising from a pair of players straddling the boundary between two runs, each retaining its strategy because either its own payoff is the larger of the two, or because its neighbour in the interior of the same run obtains a payoff even larger than the neighbour in the adjacent run. The following lemma, however, answers the question of the existence of such steady states in the negative.

Lemma 4(Stand-offs are not possible). In the ESSG on a cycle of order \(n\geq 4\) with payoff parameters \(S\) and \(T\), satisfying \(2S< T< S+1\), at least one player adjacent to the boundary between two adjacent runs of (different) strategies changes its strategy during the next game round.

Proof. By contradiction. Consider the partial game state \(X_{\ell}CDX_r\). The four players adopting these strategies are referred to as the left-most player, the cooperator, the defector and the right-most player, from left to right. For a stand-off to occur between the two central players, the cooperator and the defector, one of the following cases must occur:

1. The payoff of the cooperator equals that of the defector. This is a contradiction, because no two payoff parameters are equal in Region B of the \((S,T)\)-phase plane.
2. \(X_r=D\) and the payoff of the defector is smaller than that of the cooperator which is, in turn, smaller than that of the right-most player. In this case, the payoff of the right-most player is at most \(T\), because this player is adjacent to at least one other defector. Furthermore, the payoff of the cooperator is \(S+1\), since its payoff is larger than that of the defector. But then the payoff of the right-most player is \(2T\), a contradiction.
3. \(X_{\ell}=C\) and the payoff of the cooperator is smaller than that of the defector which is, in turn, smaller than that of the left-most player. In this case, the cooperator is adjacent to a defector and another cooperator, and so its payoff is \(S+1\). Furthermore, the payoff of the defector is \(2T\), and its payoff is greater than that of the cooperator. But then the payoff of the left-most player is more than \(2T\), a contradiction, because the largest payoff obtainable by a cooperator is \(2\).

Therefore, there can be no steady states other than the all-defector state and the all-cooperator state. That leaves only limit cycles and transient states as end state candidates. The nature of the ESSG in Region B of the \((S,T)\)-phase plane is such that cooperation runs grow and defection runs diminish in length under certain conditions. In order to establish these conditions, we first consider the situation in which there is only one defection run. The asymptotic game behaviour in this special case is formalised in the following lemma.

Lemma 5(The existence of oscillation clusters). In the ESSG on a cycle of order \(n\geq 4\) with payoff parameters \(S\) and \(T\), satisfying \(2S < T< S+1\), a game state consisting of a single defection run D of length \(d\geq 2\) and a single cooperation run C of length \(n-d\geq 2\), leads to the situation where the cooperation run grows in length by two during each round while the defection run diminishes in length by two until either the all-cooperator state is reached or a singleton defector remains. In the latter case, the defection run oscillates indefinitely between having length \(d=1\) and length \(d=3\) from round to round.

Proof. The payoff \(S+1\) of the two cooperators along the boundaries of the runs trumps the payoff \(T\) obtained by the two defectors on these boundaries. These defectors therefore cooperate during the subsequent round. Two cases are considered:

Case 1: The original length of the defection run \(d\) is even. In this case, the cooperation run continues to grow in length by two during each round until it encompasses the entire cycle.

Case 2: The original length of the defection run \(d\) is odd. In this case the cooperation run continues to grow by two until a singleton defector remains during some round \(t\). This defector obtains a payoff of \(2T\), while each adjacent cooperator obtains a payoff of \(S+1< 2T\), and so the adjacent cooperators defect during round \(t+1\). During round \(t+1\), the defection run again has length 3, so that the cooperation run again grows in length by two during round \(t+2\), yielding a singleton defector yet again. This situation is repeated indefinitely, and the set of three players centered on the singleton defector is said to form an oscillation cluster.

The above lemma establishes the existence of oscillation clusters in Region B of the \((S,T)\)-phase plane, which form an integral part of describing limit cycles and sets of transient states of the game in this region. Clearly, if the entire cycle consists of sufficiently long cooperation runs with oscillation clusters between them, the resulting state would form a limit cycle of length 2, as the game will return to that state during every second subsequent round. In such a limit cycle, the oscillation clusters will have length 1 or 3, and we accommodate this feature by referring to the phase of the oscillation cluster. One phase pertains to rounds during which the defection run has length 1 while the other phase pertains to rounds during which the defection run has length 3. The following lemma establishes the behaviour of singleton players on the cycle.

Lemma 6 (The behaviour of singleton players). In the ESSG on a cycle of order \(n \ge 3\) and with payoff parameters \(S\) and \(T\), satisfying \(2S < T < S+1\), any combination (possibly overlapping) of only the substates \(CDC\) and \(DCD\) necessarily results in the entire ensemble defecting during the next game round.

Proof. In each instance of the substate \(CDC\), each cooperator obtains a payoff of at most \(S+1\) while the defector obtains a payoff of \(2T\). The cooperators therefore necessarily defect during the next game round while the defector retains its strategy.

Similarly, in any instance of the substate \(DCD\), the cooperator obtains a payoff of \(2S\) while the defectors each obtains a payoff of at least \(T\). The cooperator therefore defects during the following game round. Two cases are finally considered to show that the defectors in the substate \(DCD\) do not change their strategy to cooperation during the following game round:

Case 1: Such a defector is adjacent to a cooperator outside of the substate \(DCD\). In this case, the payoff obtained by the defector in question is the largest payoff achievable, namely \(2T\), and so the defector retains its strategy.

Case 2: Such a defector is adjacent to a defector outside the substate \(DCD\). In this case, the payoff of the defector in question remains \(T\), while the only cooperator adjacent to it achieves a payoff of \(2S < T\). Therefore, the defector retains its strategy during the following round.

Sufficient conditions for the formation of oscillation clusters and subsequently sufficient conditions for game states being absorbed into limit cycles or sets of transient states are established next.

Lemma 7 (Sufficient conditions for the persistence of cooperation). In the ESSG on a cycle of order \(n\geq 4\) with payoff parameters \(S\) and \(T\), satisfying \(2S < T< S+1\), each game state containing at least one of the substates \(CCDD\) or \(CCCC\) eventually leads to a limit cycle or the all-cooperator steady state and, therefore, all defection is either eradicated or remains only in the form of oscillation clusters.

Proof. Every player contained in (possibly overlapping) substates of the form \(CDC\) or \(DCD\), or a substate of the form

during round \(t\) defects during round \(t+1\) --- in the substate \(CDC\), both cooperators adopt the strategy of defection and the defector retains its strategy by Lemma 6. In the substate \(CDCCCDC\), the cooperators adjacent to defectors defect during round \(t+1\) by Lemma 6, causing a formation of the substate \(DDDCDDD\), in which the cooperator and the two adjacent defectors form the substate \(DCD\) and so this cooperator defects during round \(t+2\), again by Lemma 6. Therefore, every player contained in neither the substate \(CCDD\) nor the substate \(CCCC\) will have been absorbed into a defection run of length at least 2 by round \(t+3\) at the latest, unless it already formed part of an oscillation cluster.

The substates \(CCDD\) and \(CCCC\) do not lead to defection runs, because in the former case the cooperator on the boundary between the two runs obtains a payoff \(S+1>T\) and so the defection run shrinks by one in length on that side, while in the latter case the partial state transitions to \(DCCD\) in a worst-case scenario during the next round. This worst-case scenario only occurs if singleton defectors are adjacent to the cooperation run, obtaining payoffs of \(2T>S+1\) (in the subsequent state, which features two instances of the substate \(CCDD\), the cooperation run grows in length).

By the latest during round \(t+2\), therefore, all cooperation runs will either have been eradicated or have length at least 2, while all of the defection runs already form part of oscillation clusters or have length \(d\geq2\) and so each defection run shrinks by two in length during in each round until it is either eradicated or forms an oscillation cluster.

As a result of the above lemma, each initial state either reaches the all-defector state, the all-cooperator state, or else a limit cycle or a set of transient states consisting of cooperation runs interspersed with oscillation clusters.

We now characterise those game states that lead to persistent cooperation in Region B of the \((S,T)\)-phase plane by showing that the sufficient conditions in Lemma 7 for the near-eradication of the defection strategy are, indeed, also necessary for the persistence of cooperation.

Theorem 8 (Characterisation of states leading to persistent cooperation). In the ESSG on a cycle of order \(n\geq 5\) with payoff parameters \(S\) and \(T\), satisfying \(2S < T< S+1\), a game state leads to an end state containing the strategy of cooperation if and only if it contains at least one of the substates \(CCDD\) and/or \(CCCC\).

Proof. It follows from Lemma 6 that any game state consisting only of combinations of the substates \(CDC\) and \(DCD\) (possibly with overlapping) leads to the all-defector state. Game states not consisting solely of combinations of the substates \(CDC\) and \(DCD\) (possibly with overlapping) necessarily contain one or more of the following substates:

1. \(CCDD\),
2. a run of at least four cooperators,
3. a run of three cooperators flanked by singleton defectors, or
4. a run of at least three defectors flanked by singleton cooperators.

Cases 1 and 2 above have already been shown to lead to persistent cooperation in Lemma 7.

In case 3 above, the game state contains the substate \(CDCCCDC\) during some round \(t\). In this substate, there are two instances of the substate \(CDC\) with an additional cooperator between them. By Lemma 6, each member of the substates \(CDC\) defects, while the internal cooperator retains its strategy of cooperation during round \(t+1\). This leads to the substate \(DDDCDDD\) during round \(t+1\). By Lemma 6, the cooperator defects during round \(t+2\).

In case 4 above, the game state contains the substate in (6) for some \(k \ge 3\) (this case is impossible for \(n=5\), while for \(n=6\) the substate in (6) is realised in the game state \(DCDDDC\) in which both cooperators are singletons which share an adjacent defector) during some round \(t\). By Lemma 7 all of the players in the substate will form a defection run of length \(k+4\) (length \(k+3\) for \(n=6\)) during round \(t+1.\)

5.2. Probability of persistent cooperation

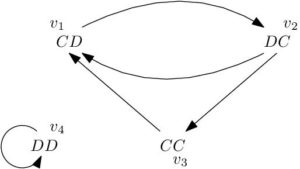
The transfer matrix method may be used to enumerate the number of states that do not lead to persistent cooperation by Theorem 8, by constructing a digraph \(D_1\) on the vertex set \(\{v_1,\ldots,v_8\}\) in which each vertex represents one of the possible binary strings of length 3 from the alphabet \(\{C,D\}\). Moreover, vertex \(v_i\), representing the string \(s_1 s_2 s_3\), is incident to vertex \(v_j\), representing the string \(s_2 s_3 s_4\), if and only if the string \(s_1 s_2 s_3 s_4\) is neither of the substates \(CCDD\) nor \(CCCC\) required for persistent cooperation in the characterisation of Theorem 8. The digraph \(D_1\) is represented graphically in Figure 5.

The adjacency matrix of \(D_1\) is

Since the determinant \(T(x)=\det(I-xB)\) is \(1-x-x^2-x^3+x^5+x^6+x^7\), where \(I\) is the identity matrix of order \(8\), it follows by the transfer matrix method [14], that the number \(b_n\) of initial game states that contain neither of the substates required for persistent cooperation on a cycle of order \(n\), as characterised in Theorem 8, satisfies the recurrence relation This recurrence relation requires seed values \(b_1^*,\dots,b_7^*\) in order to facilitate calculation of the values \(b_8\), \(b_9\), \(b_{10}\), \(\dots\) These seed values are the coefficients of the Maclaurin expansion of given by The seed values for (8) are therefore \(b_1 ^* = 1\), \(b_2 ^* =3\), \(b_3 ^* = 7\), \(b_4 ^* =11\), \(b_5 ^* = 16\), \(b_6 ^* =27\) and \(b_7 ^* = 48\). Note that these values are not the numbers of initial states that lead to the all-defection steady states of the ESSG on cycles of orders not exceeding \(7\), but are simply seed values for the recursive expression of \(b_n\) for \(n\geq 8\).

Using these seed values in conjunction with the recursive expression (8), numerical values for \(b_8\), \(b_9\), \(b_{10}\), \(\dots\) may be determined. Considering that \(b_n\) denotes the number of possible initial states of the ESSG on a cycle of order \(n\) that lead to the all-defector steady state, and that the total number of possible initial states is \(2^n\), the probability of all players eventually defecting from a randomly generated game state is \(\frac{b_n}{2^n}\). Taking the complement, the probability of persistent cooperation in the ESSG on a cycle of order \(n\) in Region B of the \((S,T)\)-phase plane of Figure 2, is given by

This probability is plotted against \(n\), the order of the underlying cycle, in Figure 6. It can be seen in the figure that this probability is increasing.

Table 3 contains the values of \(b_n\) and \(2^n\) for \(n \in\{1, \dots, 13\}\), from which it would seem that the values of \(b_n\) are increasing in \(n\), an observation which is not immediately obvious from the recurrence relation (8). The following lemma clarifies that the sequence \(b_n\) is indeed increasing.

Table 3. Values of \(b_n\) and \(2^n\) used to compute the probability \(P_B(n)=1-b_n / 2^n\) of persistent cooperation resulting from a randomly generated initial game state of the ESSG on a cycle of order \(n\), with payoff parameter values satisfying \(2S< T< S+1\).

\(n\)	1	2	3	4	5	6	7	8	9	10	11	12	13
\(b_n\)	1	3	7	11	16	27	48	80	134	228	388	659	1120
\(2^n\)	2	4	8	16	32	64	128	256	512	1024	2048	4096	8192

Lemma 9. The sequence \(b_1, b_2, b_{3}, \dots \) satisfying the recurrence relation (8) with seed values \(b_1 = 1\), \(b_2 =3\), \(b_3= 7\), \(b_4 =11\), \(b_5 = 16\), \(b_6 =27\) and \(b_7= 48\), is strictly increasing.

Proof. It is shown by the strong form of induction that \(b_n \geq \frac{6}{5} b_{n-1}\) for any natural number \(n\geq 2\). Note, as induction base case, that the statement is true for the seed values \(b_2,\dots, b_7\) and assume, as induction hypothesis, that it holds for all \(n\in \{2,\dots, k\}\), where \(k\) is some integer. Note also that \(b_n\geq0\) for all \(n\in \{2,\dots, k-1\}\) by the induction hypothesis since \(b_1=1\). It follows from (8) and repeated use of the inequality \(-b_{n-1}\geq -\frac{6}{5}b_n\) for \(n\leq k\) that \begin{equation} \begin{split} b_{k+1} &= b_{k}+b_{k-1}+b_{k-2}-b_{k-4}-b_{k-5}-b_{k-6}\\ &\geq b_k + b_{k-1}+b_{k-2}-b_{k-4}-b_{k-5}-\frac{b_{k-5}}{a}\\ &\geq b_k + b_{k-1}+b_{k-2}-b_{k-4}-\frac{a+1}{a^2}b_{k-4}\\ &\geq b_k + b_{k-1}+b_{k-2}-\frac{a^2+a+1}{a^3}b_{k-3}\\ &\geq b_k + b_{k-1}+b_{k-2}-\frac{a^2+a+1}{a^4}b_{k-2}\\ &\geq b_k + b_{k-1}-\frac{-a^4+a^2+a+1}{a^5}b_{k-1}\\ &\geq b_k-\frac{-a^5-a^4+a^2+a+1}{a^6}b_{k}\\ &= -\frac{-a^6-a^5-a^4+a^2+a+1}{a^6}b_{k}.\\ \end{split}\nonumber \end{equation} Therefore,

Since the coefficient on the right-hand side of (12) is larger than \(6/5\), it follows that \(b_{k+1} \geq \frac{6}{5}b_k\), completing the induction process.

The fact that the sequence \(P_B (1)\), \(P_B (2)\), \(P_B (3),\ldots\) is increasing may be leveraged to show that the limit of \(P_B(n)\) as \(n \to \infty\) is unity.

Theorem 10. The probability \(P_B(n)\) that a randomly generated initial state of the ESSG on a cycle of order \(n\) with payoff parameters \(S\) and \(T\), satisfying \(2S < T< S+1\), results in some form of persistent cooperation satisfies \[\lim_{n \to \infty} P_B(n) = \lim_{n \to \infty} \left(1 - \frac{b_n}{2^n}\right) = 1.\]

Proof. Setting \(L_n = b_{n-2}+b_{n-3}-b_{n-5}-b_{n-6}-b_{n-7}\) yields \(b_n = b_{n-1}+L_n\). Subtracting \(L_n\) from \(b_{n-1}\) therefore gives \begin{align*} b_{n-1} - L_n =& \ b_{n-2}+b_{n-3}+b_{n-4}-b_{n-6}-b_{n-7}-b_{n-8}- (b_{n-2}+b_{n-3}-b_{n-5}-b_{n-6}-b_{n-7})\\ =& \ b_{n-4} + b_{n-5} - b_{n-8}. \end{align*} It follows from Lemma 9 that \(b_{n-4} + b_{n-5} - b_{n-8}> 0\) and hence that \(b_{n-1} > L_n\). This means that \(0< b_n < 2b_{n-1}\). Dividing this inequality chain right through by \(2^n\) yields \[0< \frac{b_n}{2^n} < \frac{b_{n-1}}{2^{n-1}},\] from which it follows that the sequence \(\frac{b_8}{2^8}\), \(\frac{b_9}{2^9}\), \(\frac{b_{10}}{2^{10}}\), \(\dots\) remains positive and is strictly decreasing. The Monotonic Sequence Theorem [15] guarantees convergence of the sequence under these conditions.

Having established that the sequence converges, denote its limiting value by

It then follows from (8) that \begin{align*} V =& \lim_{n \to \infty} \frac{b_{n-1}+b_{n-2}+b_{n-3}-b_{n-5}-b_{n-6}-b_{n-7}}{2^n} \\ =& \lim_{n \to \infty} \frac{b_{n-1}}{2^n} + \lim_{n \to \infty} \frac{b_{n-2}}{2^n}+ \lim_{n \to \infty} \frac{b_{n-3}}{2^n} - \lim_{n \to \infty} \frac{b_{n-5}}{2^n}- \lim_{n \to \infty} \frac{b_{n-6}}{2^n} - \lim_{n \to \infty} \frac{b_{n-7}}{2^n} \\ =& \ \frac{1}{2}\lim_{n \to \infty} \frac{b_{n-1}}{2^{n-1}} + \frac{1}{2^2}\lim_{n \to \infty} \frac{b_{n-2}}{2^{n-2}}+ \frac{1}{2^3}\lim_{n \to \infty} \frac{b_{n-3}}{2^{n-3}} - \frac{1}{2^5}\lim_{n \to \infty} \frac{b_{n-5}}{2^{n-5}}- \frac{1}{2^6}\lim_{n \to \infty} \frac{b_{n-6}}{2^{n-6}} - \frac{1}{2^7}\lim_{n \to \infty} \frac{b_{n-7}}{2^{n-7}} \\ =& \left(\frac{1}{2}+ \frac{1}{2^2}+ \frac{1}{2^3} -\frac{1}{2^5}-\frac{1}{2^6}-\frac{1}{2^7}\right)\lim_{n \to \infty} \frac{b_n}{2^n}.\\ =&\left(\frac{1}{2}+ \frac{1}{2^2}+ \frac{1}{2^3} -\frac{1}{2^5}-\frac{1}{2^6}-\frac{1}{2^7}\right)V, \end{align*} which implies that \(V=0\) and consequently that \(\lim_{n \to \infty} P_B(n) = 1 - 0 = 1.\)

5.3. Fixation probabilities

The long-term asymptotic limiting nature of states of the ESSG on a cycle is investigated in this section for region B of the \((S,T)\)-phase plane in the context of a small subpopulation (size \(k\)) of players playing strategy A, being introduced into a population (size \(n-k\)) of players playing strategy B. Fixation occurs for strategy A, if the number of players playing strategy A grows considerably and is not eradicated over successive game rounds.

From Lemma 7 it is clear that instances of persistent cooperation coincide with the situation in which the strategy of defection is largely eradicated, with the possible exception of oscillation clusters remaining. Should this situation stem from a small subpopulation of cooperators being introduced into a population of defectors, we have a form of "fixation." Moreover, a small subpopulation of defectors being introduced into a population of cooperators may possibly establish themselves securely but in a situation of persistent cooperation, their existence may be limited to oscillation clusters, which does not constitute widespread growth. Therefore, "fixation" of the strategy of defection coincides with the much more stringent requirement of no persistent cooperation. As a result, we define the probability of fixation for the strategies of cooperation and defection as follows: The probability of fixation of the strategy of cooperation (defection, respectively), upon introduction of a subpopulation of \(k\) mutant cooperators (mutant defectors, respectively) into a population of \(n-k\) defectors (cooperators, respectively), is denoted by \(F_B^C(n,k)\) (\(F_B^D(n,k)\), respectively) and is the probability of persistent cooperation emerging (the probability of subsequently eradicating the strategy of cooperation, respectively). We first establish a lower bound on the fixation probability of cooperation.

Theorem 11 (Lower bound on the fixation probability of cooperation). In the ESSG on a cycle of order \(n\geq 5\) with payoff parameters \(S\) and \(T\), satisfying \(2S < T< S+1\), the fixation probability of a subpopulation of \(k< n/2\) mutant cooperators satisfies

Proof. An occurrence of the substate \(CCCC\) guarantees persistent cooperation by Theorem 8. It also guarantees that the game results in either the all-cooperator steady state or a limit cycle involving oscillation clusters. An occurrence of the substate \(CCCC\) therefore guarantees fixation of the strategy of cooperation.

In order to determine the probability of at least one occurrence of the substate \(CCCC\), when placing \(k\) cooperators randomly among a cycle of \(n-k\) defectors, consider the probability of no run of at least four cooperators resulting. This probability may be computed by considering the generating function for the number of non-negative integer solutions to the equation

with \(x_1,\dots,x_{n-k}\leq3\). The generating function for this quantity is given by For all \(n\) and \(k\), the coefficient of the term \(z^k\) in the expansion of (16) is the number of non-negative integer solutions to (15). This coefficient is The probability of not having any run of at least four cooperators is this term divided by the number of distributions of \(k\) cooperators among \(n-k\) positions with replacement --- that is, The complement of the quantity in (18) is the probability that there is at least one run of at least four cooperators.

Consider next the probability of no persistent cooperation resulting from the introduction of a small number, \(k\), of defectors into a population of \(n-k\) cooperators, with \(k< n/2\).

Theorem 12(The fixation probability of defection for small \(k\)). In the ESSG on a cycle of order \(n\geq 5\) with payoff parameters \(S\) and \(T\), satisfying \(2S < T< S+1\), the fixation probability of a subpopulation of \(k< n/4\) mutant defectors is zero.

Proof. For fixation of the strategy of defection, each defector adjacent to a pair of cooperators has to be a singleton in order to avoid the substate \(CCDD\) and similarly each cooperator adjacent to a pair of defectors has to be a singleton. The minimum number of defectors required to meet these conditions is \(n/4\), as exemplified by states of the form \(CCCDCCCD\cdots CCCD\), in which there is one defector for each triple of adjacent cooperators and for which fixation of the strategy of defection will occur by the third round. For \(k\in\{1,\ldots,n/4-1\}\), however, it follows from the pigeonhole principle there will be at least one cooperation run of length at least 4, resulting in the strategy of cooperation remaining ubiquitous, with the possible exception of the formation of oscillation clusters, by Theorem 7.

The probability of fixation resulting from the introduction of a large number of defectors into a population of cooperators is considered next.

Theorem 13(Upper bound on the fixation probability of defection for large \(k\)). In the ESSG on a cycle of order \(n\geq 5\) with payoff parameters \(S\) and \(T\), satisfying \(2S < T< S+1\), the fixation probability of a subpopulation of \(k>n/4\) mutant defectors satisfies

Proof. Consider placing \(n-k\) cooperators at \(k\) vertex locations along a cycle of order \(n\) (one to the right of each defector) and identifying the number of ways in which this may be achieved so that each cooperation run has length at most 3. This number is also the number of non-negative integer solutions to the equation \begin{equation} x_1+x_2+x_3+\cdots+x_{k}=n-k\nonumber \end{equation} in which \(x_1,\dots,x_k\leq3\), which is the coefficient of the term \(z^{n-k}\) in the generating function \begin{equation} (1-z^4)^{k}\Big(\frac{1}{1-z}\Big)^{k}.\nonumber \end{equation} This coefficient is \begin{equation} c_{n,k}=\sum_{i=0}^{k}(-1)^i{k\choose i}{n-4i-1\choose k-1}.\nonumber \end{equation} In order to obtain an upper bound on the desired fixation probability, the quantity \(c_{n,k}\) is divided by the total number of placements of \(n-k\) cooperators at \(k\) vertex locations along a cycle of order \(n\) with replacement, which is \({n-1 \choose n-k}\). This quotient is merely an upper bound on the fixation probability \(F_B^D(n,k)\) as there are instances which satisfy the aforementioned condition in which no cooperation run has length at least 4, and for which the fixation of defection is not guaranteed, such as, for example, instances containing the substate \(CCDD\).

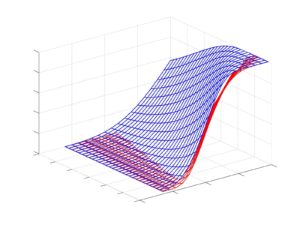
By comparing the lower bound on the fixation probability of cooperation and the upper bound on the fixation probability of defection, it may be verified that the fixation probability of cooperation is greater than that of defection for all values of \(n\) and \(k< n/2\). The strategy of cooperation is therefore favoured above that of defection in Region B of the \((S,T)\)-phase plane in the ESSG on a cycle of order \(n\). The aforementioned bounds are plotted in Figure 7.

6. Game analysis in Region C

In Region C of the \((S,T)\)-phase plane, the inequality chain \(0< T< 2S< S+1< 2< 2T\) is satisfied, and so it is clear that a singleton cooperator can now beat an adjacent defector if the defector in question is adjacent to another defector, because \(T< 2S\). This means that singleton cooperators can only be eliminated if they are flanked on both sides by singleton defectors. Should one of the defectors be adjacent to another defector, the former defector will adopt the strategy of cooperation during the following game round. In fact, the only defectors who can retain their strategy in Region C of the phase plane are defectors in the interiors of defection runs and defectors flanked by cooperators on both sides.

6.1. Characterisation of game states leading to persistent cooperation

As was the case for Region B, it can be shown in a manner akin to the proof of Lemma 4 that there also cannot be stand-offs in Region C. This means that the only steady states are again the all-defector state and the all-cooperator state. The following lemma establishes the existence of oscillation clusters in Region C.

Lemma 14(The formation of oscillation clusters). In the ESSG on a cycle of order \(n\geq4\) with payoff parameters \(S\) and \(T\), satisfying \(T < 2S < S+1\), defection runs of length at least 3 shrink by two in length during each game round until they disappear or reach length 1 and subsequently form an oscillation cluster which alternates between having length 1 and length 3.

Proof. By definition, each defection run of length at least 3 in any state other than the all-defector state is flanked on both sides by at least one cooperator (possibly the same one in the case of \(n=4\)). Defection runs of length at least 3 thus exhibit instances of the substate \(CDD\) in which the defector adjacent to the cooperator adopts the strategy of cooperation during the next game round as a result of the inequality \(T< S+1\). Each defection run of length at least 3 therefore shrinks by 2 in length during each game round until it disappears (if its original length was even) or until it has length 1 (if its original length was odd). Furthermore, the remaining defection runs of length 1 during any game round \(t\) are flanked by at least two cooperators on each side, as a cooperator was induced on each side when the defection run shrank from length 3 to length 1. Such singleton defectors obtain the largest payoff achievable, causing the defection run to grow in length to 3 during game round \(t+1\). Again by the inequality \(T< S+1\), the resulting defection run in the newly formed substate \(CDDDC\) reduces to length 1 during game round \(t+2\), and so the three central defectors of the substate form an oscillation cluster in which the length of the defection run indefinitely alternates between having length 1 and length 3.

The next result establishes the fact that there are no end states of the ESSG on a cycle in Region C of the \((S,T)\)-phase plane other than the all-defector state, the all-cooperator state and limit cycles (or sets of transient states) exhibiting oscillation clusters of the kind described in Lemma 14.

Lemma 15(Sufficient conditions for the persistence of cooperation). In the ESSG on a cycle of order \(n\geq3\) with payoff parameters \(S\) and \(T\), satisfying \(T < 2S < S+1\), a game state containing instances of the substates \(CCC\) and/or \(CDD\) leads either to the all-cooperator state or to a limit cycle or set of transient states in which all defection runs form part of oscillation clusters.

Proof. Any portion of a state not forming part of instances of the substates \(CCC\) or \(CDD\) is either a large defection run (the ends of which exhibit instances of the substate \(CDD\)) or comprises (possibly overlapping) instances of the substate \(CDC\).

In any instance of the substate \(CDC\) during some round \(t\), the defector obtains a payoff of \(2T\), the largest payoff achievable, and therefore retains its strategy while the adjacent cooperators both adopt the strategy of defection during round \(t+1\). This results in a defection run of length at least 3 flanked on both sides by cooperators (these cooperators are guaranteed at some point along the cycle due to the presence of the substates \(CCC\) and/or \(CDD\), both of which leave at least one cooperator during the following game round). During round \(t+1\), the game state is such that all defection runs have length at least 3 (except those that had length 3 or 4 during round \(t\), and have therefore already shrunk in length to 1 or 2 by round \(t+1\)). Moreover, there exists at least one cooperation run during round \(t+1\). From round \(t+1\) onwards, each defection run either already forms part of an oscillation cluster or shrinks in length by 2 during each subsequent round until it disappears or forms an oscillation cluster, by Lemma 14. If all defection runs disappear, the all-cooperator state is reached while if at least one oscillation cluster is formed, a limit cycle of length 2 or a set of transient states of cardinality 2 is reached, defined by the number, positions and phases of the oscillation clusters.

Note that the strategy of cooperation will persist in some form under the conditions of Lemma 15. We now characterise those game states that lead to persistent cooperation in Region C of the \((S,T)\)-phase plane by showing that the sufficient conditions in Lemma 15 for the persistence of cooperation are, in fact, also necessary conditions for such persistence.

Theorem 16(Characterisation of states leading to persistent cooperation). In the ESSG on a cycle of order \(n\geq 3\) with payoff parameters \(S\) and \(T\), satisfying \(T < 2S < S+1\), an end state is reached which contains the strategy of cooperation if and only if the initial state contains the substates \(CCC\) and/or \(CDD\).

Proof. Cooperation persists from one game round to the next under the conditions of the theorem, by Lemma 15. This establishes the sufficiency of these conditions. In order to establish the necessity of the conditions, note that the conditions are not satisfied only if the game state is the all-defector state or consists of portions of alternating strategies of the form \(D \alpha_1 D \alpha_2 D \cdots D \alpha_k\) where \(\alpha_i\in\{C,CC\}\) for all \(i\in\{1,\ldots,k\}\) and any natural number \(k\). Each defector therefore appears as a singleton, and so its payoff is \(2T\), strictly the largest payoff achievable. Moreover, each cooperator is adjacent to at least one defector. All cooperators therefore change their strategy to defection within a single game round.

6.2. Probability of persistent cooperation

In this section we establish the probability of persistent cooperation from a randomly generated initial game state by enumerating all possible initial states that do not lead to persistent cooperation (i.e. states that do not contain either of the substates \(CCC\) or \(CDD\) according to Theorem 16).

The directed graph \(D_2\), shown in Figure 8, contains four vertices, each representing a possible binary string of length 2. In this digraph, a vertex \(v_i\), representing the string \(s_1 s_2\), is adjacent to another vertex \(v_j\), representing the string \(s_2 s_3\), if and only if the string \(s_1 s_2 s_3\) contains neither of the substates \(CCC\) nor \(CDD\) required for persistent cooperation.

The adjacency matrix of \(D_2\) is Since \(D_2\) has two components, one of which represents the all-defector state for each \(n\), the digraph can be simplified by considering only the vertices \(v_1\), \(v_2\) and \(v_3\), thus counting the other initial states that do not lead to persistent cooperation and adding one to this tally at a later stage. The adjacency matrix of this simplified digraph, denoted by \(D^{*}_2\), is Now det(\(I-xC^{*}) = 1-x^2 -x^3\), where \(I\) is the \(3\times3\) identity matrix. Let \(c_n\) denote the number of initial states (other than the all-defector state) for the ESSG on a cycle of order \(n\) that do not lead to persistent cooperation. Then is a generating function for the sequence \(c_1\), \(c_2\), \(c_3\), \(\dots\) Furthermore, the recurrence relation may be used to calculate the value of \(c_n\) for all \(n\geq 4\). The seed values for this recurrence relation may be determined by the Maclaurin series expansion of the right-hand side of (22). The seed values to the recurrence relation (23) are therefore \(c_1 ^* = 0\), \(c_2 ^* =2\) and \(c_3 ^* = 3\). Note, therefore, that the actual number of initial states which do not lead to persistent cooperation is given by \(c_n +1\), including the all-defector state. Having established the number of possible initial states that do not lead to persistent cooperation, it follows that the number of states that do indeed allow for persistent cooperation is the complement \(2^n-c_n-1\). The probability of persistent cooperation resulting from a randomly generated assignment of strategies on a cycle of order \(n\) within the context of the ESSG in Region C is therefore Intuitively, a sequence defined as the sum of two previous, non-negative terms in the sequence is expected to be increasing, yet the fourth term of the sequence is smaller than the third, as shown in Table 4. Moreover, the sixth term is equal to the fifth.

Table 4. Values of \(c_n\) and \(2^n\) for \(n\in\{1,\ldots,10\}\) appearing in the probability expression \(P_C(n)=1-(c_n+1)/ 2^n\) of persistent cooperation resulting from a randomly generated initial state in the ESSG on a cycle of order \(n\), with payoff parameter values satisfying \(T< 2S< S+1\).

\(n \to \)	1	2	3	4	5	6	7	8	9	10
\(c_n + 1\)	1	3	4	2	5	5	7	10	12	17
\(2^n\)	2	4	8	16	32	64	128	256	512	1024

We show that the sequence is strictly increasing from the sixth term onwards.

Lemma 17. The sub-sequence \(c_6, c_7, c_8, \dots \) satisfying (23), with seed values \(c_1 = 0\), \(c_2 =2\) and \(c_3 = 3\), is strictly increasing.

Proof. By the strong form of induction over \(n\). Observe, as induction base case, that \(c_7>c_6>0\) in Table 4. Assume, as induction hypothesis, that \(c_n > c_{n-1} > 0\) for all \(n \leq k\). Finally, observe as induction step that \begin{equation} \begin{split} c_{k+1}-c_{k} &= (c_{k-1}+c_{k-2})-(c_{k-2}+c_{k-3})\\ &= c_{k-1}-c_{k-3}>0 \end{split}\nonumber \end{equation} because \(c_{k-1}>c_{k-2}>c_{k-3}\) by the induction assumption.

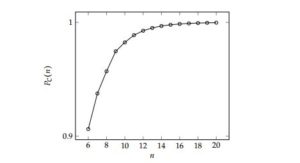
The probability of persistent cooperation in the ESSG on a cycle of order \(n\) in Region C of the \((S,T)\)-phase plane is plotted in Figure 9 as a function of \(n\).

The fact that the sequence \(P_C (6)\), \(P_C (7)\), \(P_C (8),\ldots\) is increasing may be leveraged to show that the limit of \(P_C(n)\) as \(n \to \infty\) is unity.

Theorem 18. The probability \(P_C(n)\) that a randomly generated initial state of the ESSG on a cycle of order \(n\) with payoff parameters \(S\) and \(T\), satisfying \( T < 2S < S+1\), results in some form of persistent cooperation satisfies \[ \lim_{n \to \infty} P_C(n) = \lim_{n \to \infty} \left(1 - \frac{c_n+1}{2^n} \right)= 1. \]

Proof. Setting \(J_n = c_{n-3}\) yields \(J_n = c_{n-5} + c_{n-6}\) and \(c_n = c_{n-2} + J_{n}\) by (23). Therefore,

which simplifies to \[ c_{n-2} - J_n = c_{n-4} - c_{n-6}. \] It follows from Lemma 17 that \(c_{n-4} - c_{n-6}> 0\) and hence that \(c_{n-2} > J_n\). This means that \(0< c_n < 2c_{n-2}\) and so, by Lemma 17, \(2c_{n-1}>2c_{n-2}\). Therefore, \(0< c_n < 2c_{n-1}\). Dividing the latter inequality chain right through by \(2^n\) yields \[ 0< \frac{c_n}{2^n} < \frac{c_{n-1}}{2^{n-1}}, \] from which it follows that the sequence \(\frac{c_6}{2^6}\), \(\frac{c_7}{2^7}\), \(\frac{c_8}{2^8}\), \(\dots\) remains positive and is strictly decreasing. The Monotonic Sequence Theorem [15] therefore guarantees convergence of the sequence.

Having established that the sequence converges, denote its limiting value by

It then follows from (23) that \begin{equation*} W= \lim_{n \to \infty} \frac{c_{n-2} + c_{n-3}}{2^n} = \lim_{n \to \infty} \frac{c_{n-2}}{2^n} + \lim_{n \to \infty} \frac{c_{n-3}}{2^n} = \frac{1}{2^2}\lim_{n \to \infty}\frac{c_{n-2}}{2^{n-2}} + \frac{1}{2^3}\lim_{n \to \infty} \frac{c_{n-3}}{2^{n-3}} = \left(\frac{1}{2^2}+ \frac{1}{2^3}\right)\lim_{n \to \infty} \frac{c_n}{2^n} = \left(\frac{1}{2^2}+ \frac{1}{2^3}\right)W, \end{equation*} implying that \(W=0\) and, consequently, that \(\lim_{n \to \infty} P_C(n)=1-0=1\).

This shows that the strategy of cooperation becomes more robust as the size of the population grows in the context of the ESSG on a cycle in Region C of the \((S,T)\)-phase plane.

6.3. Fixation probabilities

As in Region B, the nature of the game dynamics in Region C is such that an investigation into the traditional notion of fixation probability makes little sense. This is because complete eradication of the strategy of defection is conditioned on the lengths of defection runs which decrease as the game progresses and end either by vanishing completely or by forming oscillation clusters. The definitions of the notions of fixation probabilities of cooperation and defection in §5.3 are are therefore again adopted in the investigation of this section pertaining to Region C of the \((S,T)\)-phase plane.

Lemma 15 describes in what sense the strategy of defection remains in situations of persistent cooperation, namely within oscillation clusters. This makes it clear that in instances of persistent cooperation, the strategy of defection, although not eradicated completely, is diminished substantially. This again leads to the points of investigation: The fixation of the strategy of cooperation is examined as the probability of persistent cooperation in the context of a subpopulation of \(k\) mutant cooperators entering a population of \(n-k\) defectors. The fixation of the strategy of defection, on the other hand, is investigated as the probability of no persistent cooperation in the context of \(k< n/2\) mutant defectors being introduced into a population of \(n-k\) cooperators.

Our first result pertains to the fixation probability of the strategy of cooperation.

Theorem 19 (Fixation probability of the strategy of cooperation). In the ESSG on a cycle of order \(n\) with payoff parameters \(S\) and \(T\), satisfying \(T < 2S < S+1\), the fixation probability \(F_C^C(n,k)\) of an entering subpopulation of \(k< n/2\) mutant cooperators among a population of \(n-k\) defectors is \(F_C^C(n,k)=1\).

Proof. Arranging the players along the cycle may be thought of as placing the \(k\) cooperators and considering each of them to be holding a container on its right-hand side. The \(n-k\) defectors then have to be distributed among the \(k\) containers. For \(k< n/2\), it follows that \(n-k>k\) and so by the pigeonhole principle, there is at least one container into which at least two defectors are placed, forming an instance of the substate \(CDD\). By Lemma 15, the game will therefore result in either the all-cooperator steady state or a limit cycle of game states in which defection is only present in the form of oscillation clusters. The presence of the substate \(CDD\) consequently guarantees fixation of the strategy of cooperation.

The following theorem provides two lower bounds on the fixation probability of the strategy of defection. These bounds are achieved by disallowing the presence of the substates \(CDD\) and \(CCC\), respectively.

Theorem 20 (Fixation probability of the strategy of defection). In the ESSG on a cycle of order \(n\) with payoff parameters \(S\) and \(T\), satisfying \(T < 2S < S+1\), the fixation probability \(F_C^D(n,k)\) of an entering subpopulation of \(k< n/2\) mutant defectors among a population of \(n-k\) cooperators satisfies

and

Proof. The upper bound in (28) is the probability of no occurrences of the substate \(DD\), which is the same as occurrences of the substate \(CDD\) as the defection run containing \(DD\) must at some point be broken by a cooperation run. This probability is the number of distributions \({n-k \choose k}\) of \(k\) defectors among \(n-k\) containers along the cycle, one to the right of each cooperator, without replacement, divided by the number \({n-1 \choose k}\) of distributions (including occurrences of the substate \(DD\)) of \(k\) defectors among \(n-k\) containers along the cycle with replacement.

The upper bound in (29) is the probability of no occurrences of the substate \(CCC\). This is the number of ways in which \(n-k\) cooperators are distributed among \(k\) containers along the cycle, one to the right of each defector, without ever placing at least three cooperators in the same container, divided by the total number of ways of placing these cooperators without restriction. The number of ways of thus distributing these cooperators is number of integer solutions to the equation

\begin{equation} x_1+x_2+x_3+\dots +x_k=n-k\nonumber \end{equation} in which \(x_1\ldots,x_k\leq2\). This number is also the coefficient of \(z^{n-k}\) in the generating function The coefficient is This number is divided by \({k+n-k-1 \choose n-k}={n-1 \choose n-k}\), the number of distributions of \(n-k\) cooperators among \(k\) containers with replacement to yield the probability of no occurrences of the substate \(CCC\).

The upper bounds in (28) and (29) on the fixation probability of the strategy of defection are plotted in Figure 7 for \(n\in\{20,\ldots,50\}\) and \(k\in\{4,\ldots,20\}\). Note that each of the upper bounds dominates in a different region of the \((n,k)\)-plane, together forcing the fixation probability to be very small everywhere --- certainly smaller than 1, which means that the strategy of cooperation is favoured over the strategy of defection in Region C.

7. Conclusion

In this paper, we analysed the long-term asymptotic behaviour of the ESSG on a cycle in respect of convergence towards particular end states of the state graph. It was found that in Region A, the behaviour of the game is identical to that of the evolutionary spatial prisoner's dilemma on a cycle of the same order, in which all end states are steady states.

The remaining two regions of the \((S,T)\)-phase plane, Regions B and C, exhibit the property that no stand-offs are possible and hence there are only two steady states, namely those in which all players play the same strategy. The remaining end states either appear as limit cycles of length 2 or else as sets of transient states of cardinality 2. A set of transient states is similar to a limit cycle in appearance, but its members are both members of the same automorphism class of game states. An emergence of limit cycles and sets of transient states involving oscillation clusters in Regions B and C is interesting (Region \(A\) does not admit limit cycles). The convergence of game states towards these limit cycles or sets of transient states is characterised by a decline in length of defection runs up to the point where all the initial defectors cooperate, or singleton defectors remain which form the centres of oscillation clusters, each containing three players.

The game dynamics were fully characterised in the context of strong and global selection dynamics (previous authors focused almost entirely on weak selection or adopted a simulated approach). The results line up particularly closely with those of Eshel et al.,[9]. The differences in the methods of analysis are, however, worth noting. The update rule adopted by Burger et al., [13] was that players directly imitate the best performing player in their own neighbourhoods, rather than those of the average payoff of cooperators and defectors, respectively. This rule is simpler as it does not require the computation of a mean. The investigation we have conducted covers three payoff parameter regions in the context of the snowdrift game, while theirs took place in the context of a prisoner's dilemma and their payoff parameters were chosen on an isocline in the payoff parameter plane. The context in which Eshel et al., [9] studied mutation is richer than ours, however, as they included mutation throughout their imitation dynamics while we have included only one chance for mutation (as is usual in the study of fixation probabilities). We thus see our investigation as complementary to the work of Eshel et al., [9], and indeed note the inherent beauty in the similarity between results for the prisoner's dilemma with an average-based imitation update rule and for the snowdrift game with an update rule based on imitating the best performing player.

The investigation culminated in an analysis of the probability of persistent cooperation in the context of a random initial assignment of strategies to the players along the cycle. These probabilities were shown to tend to unity as the order of the underlying cycle increases, indicating that in larger instances of the game, some form of cooperation is almost certain to prevail, requiring only small groups of cooperators in the initial state to overcome the defectors. The investigation then turned to the context of a small subpopulation of players playing strategy \(A\) entering a population of players playing strategy \(B\) at random locations on the cycle. In this context, attention was afforded to a variation on the notion of fixation probability adapted for deterministic update rules. In Region A it was shown that the strategy of defection is favoured, while in Regions B and C, the strategy of cooperation is favoured --- this is due to the possibility of cooperation growth. The strategy of cooperation appears to be fairly robust in this setting, exhibiting resilience in respect of near-eradication and in some instances even exhibiting growth behaviour.

Alternative underlying graph structures on which to apply the same ESSG update rule, such as ladder graphs or toroidal grids, may also be of interest, especially if the graph allows for a higher degree of clustering than is possible in cycles.

Author Contributions

All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.

Conflicts of Interest

''The authors declare no conflict of interest.''