INFORMATION MENU
Full-Text PDF

Open Journal of Discrete Applied Mathematics

Vol. 5 (2022), Issue 1, pp. 25 – 28
ISSN: 2617-9687 (Online) 2617-9679 (Print)
DOI: 10.30538/psrp-odam2022.0067

TEMO theorem for Sombor index

Ivan Gutman
Faculty of Science, University of Kragujevac, Kragujevac, Serbia; gutman@kg.ac.rs

Copyright © 2022 Ivan Gutman. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received: December 4, 2021 – Accepted: March 17, 2022 – Published: April 10, 2022

Abstract

TEMO = topological effect on molecular orbitals was discovered by Polansky and Zander in 1982, in connection with the eigenvalues of molecular graphs. Eventually, analogous regularities were established for a variety of other topological indices. We now show that a TEMO-type regularity also holds for the Sombor index (\(SO\)): For the graphs \(S\) and \(T\), constructed by connecting a pair of vertex-disjoint graphs by two edges, \(SO(S) < SO(T)\) holds. Analogous relations are verified for several other degree-based graph invariants.

Keywords:

Sombor index; TEMO; Degree (of vertex); Vertex-degree-based graph invariant.

1. Introduction

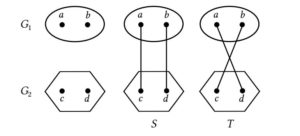
In this paper, we consider a pair of graphs that traditionally are denoted by \(S\) and \(T\). These are constructed by starting with any two vertex-disjoint graphs \(G_1\) and \(G_2\). Let \(a\) and \(b\) be two distinct vertices of \(G_1\), and let \(c\) and \(d\) be two distinct vertices of \(G_2\). Then \(S\) is the graph obtained from \(G_1\) and \(G_2\) by connecting \(a\) with \(c\) and \(b\) with \(d\). The graph \(T\) is obtained analogously, by connecting \(a\) with \(d\) and \(b\) with \(c\), see Figure 1.

Figure 1. The structure of the graphs \(S\) and \(T\) and the labeling of their vertices.

In 1982, Polansky and Zander discovered a remarkable property of the graphs \(S\) and \(T\) [1]. They established that the characteristic polynomials of \(S\) and \(T\) are related as \[ \phi(T,\lambda) - \phi(S,\lambda) = \big[ \phi(G_1-a,\lambda) - \phi(G_1-b,\lambda) \big] \big[ \phi(G_2-c,\lambda) - \phi(G_2-d,\lambda) \big]\,. \] In the special case when \(G_1 \cong G_2\), \[ \phi(T,\lambda) - \phi(S,\lambda) = \big[ \phi(G_1-a,\lambda) - \phi(G_1-b,\lambda) \big]^2\,, \] which means that the inequality
\begin{equation} \label{1} \phi(T,\lambda) \geq \phi(S,\lambda) \end{equation}
(1)
holds for all real values of the variable \(\lambda\).

The inequality (1) implies certain regularities for the distribution of the eigenvalues of \(S\) and \(T\) [2,3,4] and have appropriate (experimentally verifiable) consequences on the distribution of the molecular orbital energy levels [5]. The authors of [1] called this a '' topological effect on molecular orbitals'' and used the acronym TEMO. Eventually, TEMO was extensively investigated; a detailed bibliography of this research can be found in the books [6,7].

After the discovery of the regularities between the eigenvalues of \(S\) and \(T\), a number of other TEMO-like relations for these pairs of graphs was discovered [8,9,10,11,12,13,14,15,16].

2. TEMO for Sombor index

The Sombor index (\(SO\)) is a recently conceived vertex-degree-based graph invariant [17], that already attracted much attention (see, e.g. [18,19,20,21,22]). It is defined as
\begin{equation} \label{3} SO = SO(G) = \sum_{uv \in \mathbf E(G)} \sqrt{\delta_u^2 + \delta_v^2}\,, \end{equation}
(2)
where \(\delta_u\) is the degree (= number of first neighbors) of the vertex \(u\), \(uv\) denotes the edge connecting the vertices \(u\) and \(v\), and the summation goes over all edges of the underlying graph \(G\).

In what follows, we establish a TEMO-like property of the Sombor index, i.e., investigate the relation between \(SO(S)\) and \(SO(T)\).

Denote by \(\delta_a,\delta_b,\delta_c,\delta_d\) the degrees of the vertices \(a,b,c,d\) of the graphs \(S\) and \(T\) (see Fig. 1). It is obvious that if either \(\delta_a=\delta_b\) or \(\delta_c=\delta_d\) or both, then \(SO(S)=SO(T)\). Therefore, we consider the case \(\delta_a \neq \delta_b\) and \(\delta_c \neq \delta_d\). Without loss of generality, we may assume that \(\delta_a > \delta_b\) and \(\delta_c > \delta_d\).

Theorem 1. Let \(G_1\) and \(G_2\) be arbitrary vertex-disjoint graphs and \(a,b,c,d\) their vertices as indicated in Figure 1. If \(\delta_a > \delta_b\) and \(\delta_c > \delta_d\), then \(SO(S) < SO(T)\).

Note that the degree of the vertex \(a\) in the graph \(G_1\) is \(\delta_a-1\), etc.

Proof. Observe first that \begin{eqnarray*} SO(S) & = & \sqrt{\delta_a^2+\delta_c^2} + \sqrt{\delta_b^2+\delta_d^2} + SO^\ast\,, \\ SO(T) & = & \sqrt{\delta_a^2+\delta_d^2} + \sqrt{\delta_b^2+\delta_c^2} + SO^\ast\,, \end{eqnarray*} where \(SO^\ast\) is the sum of the terms \(\sqrt{\delta_u^2 + \delta_v^2}\) over other edges of \(S\) or \(T\). Thus, \[ SO(S)-SO(T) = \sqrt{\delta_a^2+\delta_c^2} + \sqrt{\delta_b^2+\delta_d^2} - \sqrt{\delta_a^2+\delta_d^2} - \sqrt{\delta_b^2+\delta_c^2}\,. \] It needs to be demonstrated that

\begin{equation} \label{2} \sqrt{\delta_a^2+\delta_d^2} + \sqrt{\delta_b^2+\delta_c^2} > \sqrt{\delta_a^2+\delta_c^2} + \sqrt{\delta_b^2+\delta_d^2}\,. \end{equation}
(3)
In order to achieve this goal, consider \[ Q = \big( \delta_a^2-\delta_b^2 \big)\big( \delta_c^2-\delta_d^2 \big)\,, \] which by the assumptions made in the statement of Theorem 1 is evidently positive-valued. \begin{eqnarray*} Q > 0 & \Longleftrightarrow & \delta_a^2\,\delta_c^2 + \delta_b^2\,\delta_d^2 > \delta_a^2\,\delta_d^2 + \delta_b^2\,\delta_c^2 \\ & \Longleftrightarrow & \delta_a^2\,\delta_b^2 + \delta_c^2\,\delta_d^2 + \delta_a^2\,\delta_c^2 + \delta_b^2\,\delta_d^2 > \delta_a^2\,\delta_b^2 + \delta_c^2\,\delta_d^2 + \delta_a^2\,\delta_d^2 + \delta_b^2\,\delta_c^2 \\ & \Longleftrightarrow & \big(\delta_a^2+\delta_d^2 \big)\big(\delta_b^2+\delta_c^2 \big) > \big(\delta_a^2+\delta_c^2 \big)\big(\delta_b^2+\delta_d^2 \big) \\ & \Longleftrightarrow & 2 \sqrt{\big(\delta_a^2+\delta_d^2 \big)\big(\delta_b^2+\delta_c^2 \big)} > 2 \sqrt{\big(\delta_a^2+\delta_c^2 \big)\big(\delta_b^2+\delta_d^2 \big)} \\ & \Longleftrightarrow & \big( \delta_a^2+\delta_d^2 \big) + \big( \delta_b^2+\delta_c^2 \big) + 2 \sqrt{\big(\delta_a^2+\delta_d^2 \big)\big(\delta_b^2+\delta_c^2 \big)} > \big( \delta_a^2+\delta_c^2 \big) + \big( \delta_b^2+\delta_d^2 \big) + 2 \sqrt{\big(\delta_a^2+\delta_c^2 \big)\big(\delta_b^2+\delta_d^2 \big)} \\ & \Longleftrightarrow & \Big( \sqrt{\delta_a^2+\delta_d^2} + \sqrt{\delta_b^2+\delta_c^2} \Big)^2 > \Big( \sqrt{\delta_a^2+\delta_c^2} + \sqrt{\delta_b^2+\delta_d^2} \Big)^2 \end{eqnarray*} which directly implies the inequality (3).

3. More TEMO-type relations

In an analogous, yet slightly easier, manner, we can verify the following TEMO-type results.

Using the notation of Eq. (2), the second Zagreb index \(M_2\), the Randic index \(R\), the reciprocal Randic index \(RR\), and the nirmala index \(N\) are, respectively, defined as [23,24,25,26]

\begin{eqnarray*} M_2 = M_2(G) & = & \sum_{uv \in \mathbf E(G)} \delta_u\,\delta_v \,,\\ R = R(G) & = & \sum_{uv \in \mathbf E(G)} \frac{1}{\sqrt{\delta_u\,\delta_v}}\,, \\ RR = RR(G) & = & \sum_{uv \in \mathbf E(G)} \sqrt{\delta_u\,\delta_v} \,,\\ N = N(G) & = & \sum_{uv \in \mathbf E(G)} \sqrt{\delta_u+\delta_v}\,. \end{eqnarray*}

Theorem 2. Let \(G_1\) and \(G_2\) be arbitrary vertex-disjoint graphs and \(a,b,c,d\) their vertices as indicated in Figure 1. If \(\delta_a > \delta_b\) and \(\delta_c > \delta_d\), then

  • (a) \(M_2(S) > M_2(T)\),
  • (b) \(R(S) > R(T)\),
  • (c) \(RR(S) > RR(T)\),
  • (d) \(N(S) < N(T)\).

Analogous relations hold also for the reduced versions of these indices, in which \(\delta\) is replaced by \(\delta-1\).

Conflicts of Interest:

The author declares no conflict of interest.

References

  1. Polansky, O. E., & Zander, M. (1982). Topological effect on MO energies. Journal of Molecular Structure, 84, 361-385. [Google Scholor]
  2. Graovac, A., Gutman, I., & Polansky, O. E. (1985). An interlacing theorem in simple molecular-orbital theory. Journal of Chemical Society Faraday Transactions 2, 81, 1543-1553. [Google Scholor]
  3. Gutman, I., Graovac, A., Polansky, O. E. (1985). On the theory of \(S\)- and \(T\)-isomers. Chemical Physics Letters, 116, 206-209. [Google Scholor]
  4. Gutman, I., Graovac, A., Polansky, O. E. (1988). Spectral properties of some structurally related graphs. Discrete Applied Mathematics, 19, 195-203. [Google Scholor]
  5. Polansky, O. E. (1984). Topological effects displayed in absorption and photoelectron spectra. Journal of Molecular Structure, 113, 281-298. [Google Scholor]
  6. Gutman, I. (2017). Selected Theorems in Chemical Graph Theory. Kragujevac: Univ. Kragujevac. [Google Scholor]
  7. Polansky, O. E., Mark, G., & Zander, M. (1987). Der topologische Effekt an Molekülorbitalen (TEMO) - Grundlagen und Nachweis. Mülheim: Max Planck Institut für Strahlenchemie. [Google Scholor]
  8. Elkin, V. (1988). Some topological properties of two types of S,T-isomers. MATCH Communications in Mathematical and in Computer Chemistry, 23, 153-162. [Google Scholor]
  9. Elkin, V., & Li, X. (1992). Topological properties of some novel S,T-isomers (I). MATCH Communications in Mathematical and in Computer Chemistry, 28, 277-286. [Google Scholor]
  10. Graovac, A., Gutman, I., & Polansky, O. E. (1984). Topological effect on MO energies, IV. The total \(\pi\)-electron energy of \(S\)- and \(T\)-isomers. Monatshefte für Chemie, 115, 1-13. [Google Scholor]
  11. Li, X., & Zheng, S. (1994). The copositive property of a type of cubic forms and an application in the comparison of S,T-isomers. MATCH Communications in Mathematical and in Computer Chemistry, 30, 189-201. [Google Scholor]
  12. Li, X. (1994). Topological properties of some novel S,T-isomers. II. MATCH Communications in Mathematical and in Computer Chemistry, 30, 179-188. [Google Scholor]
  13. Yang, Y., & Klein, D. J. (2014). Comparison theorems on resistance distances and Kirchhoff indices of S,T-isomers. Discrete Applied Mathematics, 175, 87-93. [Google Scholor]
  14. Zhang, H. (1993). The Clar covering polynomials of S,T-isomers. MATCH Communications in Mathematical and in Computer Chemistry, 29, 189-197. [Google Scholor]
  15. Zhang, F., & Chen, Z. (1986). Some topological properties of two types of S,T-isomers. MATCH Communications in Mathematical and in Computer Chemistry, 21, 187-194. [Google Scholor]
  16. Zhang, F., & Chen, Z. (1993). Some topological properties of two types of radical S,T-isomers. MATCH Communications in Mathematical and in Computer Chemistry, 29, 199-207. [Google Scholor]
  17. Gutman, I. (2021). Geometric approach to degree-based topological indices: Sombor indices. MATCH Communications in Mathematical and in Computer Chemistry, 86, 11-16.[Google Scholor]
  18. Rada, J., Rodríguez, J. M., & Sigarreta, J. M. (2021). General properties on Sombor indices. Discrete Applied Mathematics, 299, 87-97. [Google Scholor]
  19. Horoldagva, B., & Xu, C. (2021). On Sombor index of graphs. MATCH Communications in Mathematical and in Computer Chemistry, 86, 793-713. [Google Scholor]
  20. Kulli, V. R. (2021). Sombor index of certain graph operators. International Journal of Engineering Sciences & Research Technology, 10(1), 127-134. [Google Scholor]
  21. Shang, Y. (2022). Sombor index and degree-related properties of simplicial networks. Applied Mathematics and Computation, 419, #126881, https://doi.org/10.1016/j.amc.2021.126881. [Google Scholor]
  22. Gutman, I. (2021). Some basic properties of Sombor indices. Open Journal of Discrete Applied Mathematics, 4(1), 1-3. [Google Scholor]
  23. Gutman, I., Furtula, B., & Elphick, C. (2014). Three new/old vertex-degree-based topological indices. MATCH Communications in Mathematical and in Computer Chemistry 72, 617-632.[Google Scholor]
  24. Gutman, I., Rušcic, B., Trinajstic, N., & Wilcox, C. F. (1975). Graph theory and molecular orbitals. XII. Acyclic polyenes. Journal of Chemical Physics, 62, 3399-3405.[Google Scholor]
  25. Kulli, V. R. (2021). Nirmala index. International Journal of Mathematics Trends and Technology, 67(3), 8-12. [Google Scholor]
  26. Randic, M. (1975). On characterization of molecular branching. Journal of the American Chemical Society, 97, 6609-6615.[Google Scholor]
Category: ODAM - Vol 5 - Issue 1 (2022)