Open Journal of Mathematical Analysis
ISSN: 2616-8111 (Online) 2616-8103 (Print)
DOI: 10.30538/psrp-oma2020.0050
Analysis and numeric of mixed approach for frictional contact problem in electro-elasticity
Univ. Hassan 1, Laboratory MISI, 26000 Settat, Morocco.; (M.B & E.E & A.Z)
Cadi Ayyad University, Polydisciplinary Faculty, Department of Mathematics and Computer Science, B.P. 4162 Safi, Morocco.; (M.B)
\(^1\)Corresponding Author: bouallalamustaphaan@gmail.com
Abstract
Keywords:
1. Introduction
The numerical study of the piezoelectric [1, 2] contact problems [3, 4, 5, 6, 7] presents a great challenges, because the non coercivity and non differentiability of some terms. The linear term coupling the mechanical field and electric potential is non coercive and non symmetric. The term corresponding to the friction is convex and non differentiable, in the variational formulation in one hand. In the other hand, the non-linear coupling mechanical field and frictional contact, it can be shown in the norm of the tangential component of the mechanical field present in the frictional function.
To overcome these difficulties, the authors develop some methods like finite elements method [8, 9], penalty method and fixed point method [4]. The most and sufficient method for this type of problem is the ones based on convex duality [10] and the introduction of Lagrange multipliers [11, 12, 13]. Primal-dual active sets strategy, which is an equivalent to infinite dimensional semismooth Newton method, is applied in [14] while in [15] the author propose a numerical approximation and based Uzawa block relaxation method. Alternating directions method of multipliers (ADMM) is based in [16].
In mechanic of structures one is always interested in the determination of the stress tensor \(\sigma\) more than the mechanical displacement itself. Methods have been developed for calculate an approximation of \(\sigma\) from \(u\) and the drawback is not easy to build an approximation space of tensors satisfying the equilibrium relations and required regularity. A mixed variational formulation have been developed to handle this difficulty. Concerning the piezoelectric contact problems, mixed formulation were developed in [17, 18, 19].
In this paper, we introduce a mixed variational approach based Lagrange multipliers which describes the static frictional contact between a piezoelectric body and non-conductive foundation. The standard mixed variational formulation of contact problems is formally in the following form [17, 18, 20]:
The idea consists in decoupling the contact from the friction by introducing two convex sets, one is reserved to the contact multiplier and the second is stated for the friction. This approach leads to decoupled inequalities in mixed variational problem. Since \(a(\cdot,\cdot)\) is not symmetric we follow the standards techniques and steps based on [17,18 ] but with different fixed point map (\(Step\, 3\) in the proof) and hence more analysis is needed to get the existence and uniqueness result. The resulting problem is an system by blocks of two unknowns (displacement and potential), regarding its structure and the form of blocks we use Gauss elimination technique and then we obtain a Schur complement in the matrix corresponding to displacement subproblem. It is well known (see [16, 21]) that this technique allows a suitable preconditioner for conjugate gradient method employed to solve the resulting symmetric and positive definite system.
To prove the efficiency of this approach, we state suitable numerical fixed point scheme. The convergence is proved basing abstract perturbed problem and fixed point process, Banach fixed point is hence applied. For details concerning the mathematical tools we refer to [22, 23, 24, 25].
The paper is structured as: In Section 2, we present the model of equilibrium process of the elastic piezoelectric body in frictional contact with a non-conductive foundation,we introduce the functional spaces for various quantities, list the assumptions on given data and derive the weak formulation of the problem. In Section, 2.2 we state and prove our main existence and uniqueness result, Theorem 1. The proof of these theorem are carried out in several steps and are based on an abstract result in the study of elliptic variational inequalities and Banach fixed point technique. The successive iterative method is detailed followed by the convergence result in Section 4. In Section 5, we conclude with finite element discretization and we give some numerical experiments by simple example .
2. Problem setting and main results
2.1. Problem setting
The piezoelectric body occupies in its reference configuration (initial configuration) the domain \(\Omega\subset\mathbb{R}^{d}\), \(d=2,3\). We suppose that \(\Omega\) is bounded with a smooth (enough) boundary \(\partial \Omega=\Gamma\). We denote by \(n\) be the outer normal to \(\Gamma\) and summation over repeated indices is implied and the index that follows a comma represents the partial derivative with respect to the corresponding component of the variable. The indices take values in \(\{1,\,\cdots,\,d\}\) the summation convention over repeated indices is used.
Below we use \(\mathbb{S}^{d}\) to denote the space of second order symmetric tensors on \(\mathbb{R}^{d}\) while "\(.\)" and \(\| \cdot \|\) will denote the inner product and the Euclidean norm on \(\mathbb{S}^{d}\) and \(\mathbb{R}^{d}\), that is \begin{eqnarray*}u. v=u_{i}v_{i}, \hspace{1cm}\|v\|=(v. v)^{\frac{1}{2}},\hspace{0.5cm}\forall\;\; u,v\in \mathbb{R}^{d},\\ \sigma. \tau=\sigma_{ij}\tau_{ij}, \hspace{1cm}\|\tau\|=(\tau.\tau)^{\frac{1}{2}},\hspace{0.5cm}\forall\;\; \sigma,\tau\in \mathbb{S}^{d}.\end{eqnarray*}
We also use the notations \(u_{n}\) and \(u_\tau\) for the normal and tangential displacement, that is \(u_{n}=u. n\) and \(u_\tau=u-u_{n}n\). Similarly we denote by \(\sigma_{n}\) and \(\sigma_\tau\) the normal and tangential stress tensor given by \(\sigma_{n}=\sigma n. n\), \(\sigma_\tau=\sigma n-\sigma_{n}n\).\\ We introduce the following functional spaces on \(\Omega\); \begin{eqnarray*} &&H= L^{2}(\Omega)^{d}=\left\lbrace u=(u_{i})\; | \;u_{i}\in L^{2}(\Omega)\right\rbrace ,\;\;\; \mathcal{H}= \left\lbrace \sigma = \sigma_{ij},\; \sigma_{ij}=\sigma_{ji}\in L^{2}(\Omega)\right\rbrace, \\ &&H_{1}=\left\lbrace u \in H\; | \;\epsilon(u) \in \mathcal{H}\right\rbrace ,\;\;\;\mathcal{H}_1= \left\lbrace \sigma \in \mathcal{H}\;|\; Div \;\sigma \in H \right\rbrace \end{eqnarray*} endowed with the inner products \begin{eqnarray*}&&(u,v)_{H}=\int_{\Omega} u_{i}v_{i}dx,\hspace{0.5cm} (\sigma,\tau)_{\mathcal{H}}=\int_{\Omega} \sigma_{ij}\tau_{ij}dx.\\ &&(u,v)_{H_{1}}= (u,v)_{H}+(\varepsilon(u),\varepsilon(v))_{\mathcal{H}},\hspace{0.5cm} (\sigma,\; \tau)_{\mathcal{H}_{1}}=(\sigma,\; \tau)_{\mathcal{H}}+(Div\; \sigma,\; Div\; \tau)_{H} .\end{eqnarray*}
The associated norms on the spaces \(H\), \(\mathcal{H}\), \(H_{1}\) and \(\mathcal{H}_{1}\) are denoted by \(\|.\|_{H}\), \(\|.\|_{\mathcal{H}}\), \(\|.\|_{H_{1}}\) and \(\|.\|_{\mathcal{H}_{1}}\) respectively. We recall the well known Green's formula $$ \left( \sigma,\varepsilon(v) \right)_{\mathcal{H}} + \left( Div \; \sigma,v \right)_{H} = \int_{\Gamma} \sigma n. v \; da \;\;\forall\;\; v \in H_{1}, $$ where \(Div \; \sigma = (\sigma_{ij,j})\) and for more details of this formula see [24].In addition we shall use the following notations. \(u\) is the displacement field , \(\varepsilon (u)=(\varepsilon_{ij}(u))\) to denote the strain tensor, given by \(\varepsilon_{ij}(u)=\frac{1}{2}(u_{i,j}+u_{j,i})\) and \(\sigma =(\sigma_{ij})\) being the stress tensor. Lets \(\varphi\) denote the electric potential, \(E(\varphi)=(E_{i}(\varphi))\) is the electric field, which is defined by \(E_{i}(\varphi)=-\varphi_{,i}\) and \(D=(D_{i})\) is the electric displacement field.
The equilibrium equations are given by
To give the mechanical and electrical boundary conditions, we subdivide \(\Gamma\) into three disjoints measurable parts \(\Gamma_{1},\Gamma_{2},\Gamma_{3}\) such that \(meas(\Gamma_{1})>0\). The body is assumed to be clamped on \(\Gamma_{1}\) and surfaces traction of density \(f_{2}\) act on \(\Gamma_{2}\), on \(\Gamma_{3}\) the body can reaches a frictional contact with the so called foundation (insulating foundation). A second partition of \(\Gamma\), that is \(\Gamma=\Gamma_{3}\cup\Gamma_{a}\cup \Gamma_{b}\). Surface electric charge of density \(q_{2}\) acts on \(\Gamma_{_{b}}\), and the electric potential vanishes on \(\Gamma_{b}\). We use the same symbol \(v\) for the trace of \(v\) on \(\Gamma\).
Problem 1. Find the displacement field \(u:\Omega\longrightarrow \mathbb{R}^{d}\) and the electric potential field \(\varphi:\Omega\longrightarrow \mathbb{R}\) such that (2)-(12) hold.
To study of Problem 1 we will assume, under Einstein summation convention, that:Let us introduce the following Hilbert spaces: $$V=\left\lbrace v\in [H^{1}(\Omega)]^{d}/v=0\text{ on }\Gamma_{1}\right\rbrace, $$ $$W=\left\lbrace \varphi\in H^{1}(\Omega)/\varphi =0\text{ on }\Gamma_{a}\right\rbrace, $$ $$K=\left\lbrace v\in [H^{\frac{1}{2}}(\Gamma_{3})]^{d}/v_{n}\leq g\text{ on }\Gamma_{3}\right\rbrace.$$
If \(u\) and \(\varphi\) are regular functions which satisfy (2)-(10), then we find: $$\int_{\Omega}\mathcal{A}\varepsilon(u)\varepsilon(v)dx+\int_{\Omega}\mathcal{B}^*\nabla \varphi\varepsilon(v) dx=\int_{\Omega}f_{0}vdx+\int_{\Gamma_{2}}f_{2}vd\Gamma+\int_{\Gamma_{3}}(\sigma n).vd\Gamma$$
$$-\int_{\Omega}\mathcal{B}\varepsilon(u)\nabla \psi dx +\int_{\Omega}\beta \nabla \varphi\nabla \psi dx=\int_{\Omega}q_{0}\psi dx-\int_{\Gamma_{b}}q_{2}\psi d\Gamma .$$ Let us introduce the functional space \(\tilde{V}=V\times W\), which is the Hilbert space endowed with the inner product:\((\tilde{u},\tilde{v})_{\tilde{V}}=(u,v)_{V}+(\varphi,\psi )_{W}\) where \(\tilde{u}=(u,\varphi ),\;\tilde{v}=(v,\psi )\in \tilde{V}\). Let \( a:\tilde{V}\times\tilde{V}\longrightarrow\mathbb{R}\) be the bi-linear form given by: \(\displaystyle{a(\tilde{u},\tilde{v})=\int_{\Omega}\mathcal{A}\varepsilon(u)\varepsilon(v)dx+\int_{\Omega}\mathcal{B}^*\nabla \varphi\varepsilon(v) dx -\int_{\Omega}\mathcal{B}\varepsilon(u)\nabla \psi dx +\int_{\Omega}\beta\nabla \varphi \nabla \psi dx}.\) Moreover, by Riesz's representation theorem, we define \(\tilde{f}\in\tilde{V}\) by: $$(\tilde{f},\tilde{v})_{\tilde{V}}:=\int_{\Omega}f_{0}vdx+\int_{\Gamma_{2}}f_{2}vd\Gamma +\int_{\Omega}q_{0}\psi dx-\int_{\Gamma_{b}}q_{2}\psi d\Gamma.$$ Using the previous tools, we find: $$a(\tilde{u},\tilde{v})=(\tilde{f},\tilde{v})_{\tilde{V}}+\int_{\Gamma_{3}}(\sigma n).vd\Gamma.$$ Since \((\sigma n).v=\sigma_\tau v_\tau+\sigma_{n}v_{n}\), then: $$a(\tilde{u},\tilde{v})=(\tilde{f},\tilde{v})_{\tilde{V}}+\int_{\Gamma_{3}}\sigma_\tau v_\tau+\sigma_{n}v_{n}d\Gamma.$$ Let \(H_\Gamma^{*}\) be the dual space of the space \(H_\Gamma=[H^{\frac{1}{2}}(\Gamma_{3})]^{d}\) and let us define
It is straightforward that \(M_{T,N}\) are two closed convex sets of \(H_\Gamma^{*}\) and \(0_{H_\Gamma^{*}}\in M_{N,T}\). We introduce two dual Lagrange multipliers \(\lambda_N\) and \(\lambda_T \in M\) as follows: $$\left\langle \lambda_N, v\right\rangle_{\Gamma_{3}}:=-\int_{\Gamma_{3}}\sigma_{n}v_{n}d\Gamma ,\hspace{0.5cm}v\in V, \; \text{and}\;\left\langle \lambda_T, v\right\rangle_{\Gamma_{3}}:=-\int_{\Gamma_{3}}\sigma_\tau v_\tau d\Gamma , \hspace{0.5cm}v\in V.$$
We define two bi-linear and continuous forms \(b_{1}\) and \(b_{2}\) for all \(v \in V,\; \delta_{1}, \delta_{2} \in H_\Gamma^{*}\) as follows: $$b_{1}: \tilde{V} \times H_\Gamma^{*} \longrightarrow \mathbb{R},\hspace{1cm}b_{1}(\tilde{v},\delta_{1}):=\left\langle \delta_{1} ,v \right\rangle_{\Gamma_{3}},$$ $$b_{2}:\tilde{V} \times H_\Gamma^{*} \longrightarrow \mathbb{R},\hspace{1cm}b_{2}(\tilde{v},\delta_{2}):=\left\langle \delta_{2} ,v \right \rangle_{\Gamma_{3}}.$$
We see that \(\displaystyle{b_{1}(\tilde{u},\lambda_N)=-\int_{\Gamma_{3}}\sigma_{n}u_{n}d\Gamma}\), and by definition of \(M_{N}\) we have: $$ b_{1}(\tilde{u},\delta_{1}-\lambda_N)\leq 0,\hspace{1cm} \forall\;\; \delta_{1} \in M_{N}. $$ Also, taking into account the definition of \(M_T\), \(\lambda_T\), and the assumption (10), we have: $$b_{2}(\tilde{u},\lambda_T)=\left\langle \lambda_T, u\right\rangle_{\Gamma_{3}}=-\int_{\Gamma_{3}}\sigma_\tau u_\tau d\Gamma.$$ Keeping in mind that the Sobolev trace operator is linear and continuous, it is clear that there exists \(M_{b_{i}}>0\) such that:Problem 2.(Weak formulation of Problem Problem 1) Find \(\tilde{u}\in\tilde{V}\) and \(\lambda=(\lambda_N,\lambda_T)\in M_{N}\times M_{T}(\mathcal{F}\lambda_N)\) such that:
2.2. Main results
In this section we present our main results.Theorem 1. Assume (13)-(17), then the Problem 2 has unique solution \((\tilde{u},\lambda)\in\tilde{V}\times M\). Moreover if \((\tilde{u}_{1},\lambda)\) and \((\tilde{u}_{2},\beta)\) are two solutions of Problem 2 for given data \(\tilde{f}_{1}\) and \(\tilde{f}_{2}\) respectively, then $$||\tilde{u}_{1}-\tilde{u}_{2}||_{\tilde{V}}+||\lambda -\beta||_{H_\Gamma^{*} \times H_\Gamma^{*}}\leq C(||\tilde{f}_{1}-\tilde{f}_{2}||).$$
We denote \(b_{1}(v,\delta_{1})+b_{2}(v,\delta_{2})=\left\langle \delta_{1}, v\right\rangle_{\Gamma_{3}}+\left\langle \delta_{2}, v\right\rangle_{\Gamma_{3}}=\left\langle \delta_{1}+\delta_{2}, v\right\rangle_{\Gamma_{3}}\), hence there exists \(\alpha >0\) such thatProposition 1. Let \((u^{\ell},\lambda^\ell)\) be the solution generated by the Algorithm 1, then
3. Proof of the main result
Let \(X\) and \(Y\) two Hilbert spaces endowed with the inner product \((\cdot,\cdot)_{X}\) and \((\cdot,\cdot)_{Y}\) respectively and let us consider two bi-linear forms as follows:\(a(\cdot,\cdot):X\times X\longrightarrow\mathbb{R}\), generally non symmetric, such that
Problem 3. For given \(f\in X\), find \(u\in X\) and \(\lambda=(\lambda_N,\lambda_T)\in M\) such that:
Theorem 2. Let \(f \in X\) and assume that (30)-(34) hold. Then, there exists a unique solution \((u,\lambda)\) of \textbf{Problem \(AWF\)} Moreover, if \((u_{1},\lambda)\) and \((u_{2},\gamma)\) are two solutions of the \textbf{Problem \(AWF\)} for given data functions \(f_{1}\in X\) and \(f_{2}\in X\) respectively, then, there exists \(SC>0\) such that:
Proof.
We consider the symmetric \(a_{0}(.,.)\) and anti-symmetric \(c(.,.)\) part of \(a(.,.)\) respectively, defined by
$$a_{0}:X\times X\longrightarrow \mathbb{R} ,\;\;a_{0}(u,v):=(a(u,v)+a(v,u))/2,\hspace{1cm}u, \forall\;\; v\in X,$$
$$c:X\times X\longrightarrow \mathbb{R} , \;\;c(u,v):=(a(u,v)-a(v,u))/2,\hspace{1cm}u,\forall\;\; v\in X.$$
For given \(0
Problem 4. (Auxiliary perturbed problem) For given \(f\in X\), find \(u\in X\) and \(\lambda \in M \), such that \begin{eqnarray} a_{t}(u,v)+b(v,\lambda)=(f,v)_{X},\hspace{1cm}\forall\;\; v\in _{X},\label{3.11} \\ b_{1}(u,\delta-\lambda_N)\leq 0,\hspace{1cm}\forall\;\; \delta\in M_N,\label{3.12} \\ b_{2}(u,\delta-\lambda_T)\leq 0,\hspace{1cm}\forall\;\; \delta\in M_T.\label{3.13} \end{eqnarray}
The rest of the proof will be treated by steps.Step 1.
If \(t=0\), the Problem 4 has unique solution. Indeed, if \(l=0\) the problem is equivalent to the saddle point problem: find \(u\in X\) and \(\lambda\in M\) such that $$\mathcal{L}(u,\delta)\leq \mathcal{L}(u,\lambda) \leq\mathcal{L}(v,\lambda),\hspace{1cm}\forall\;\; v\in X,\delta\in M,$$ where \(\mathcal{L}:X\times M \longrightarrow\mathbb{R}\) is defined by:\\ \(\begin{array}{ccc} \mathcal{L}(v,\delta)&:=& \dfrac{1}{2}a_{0}(v,v)-(f,v)_{X}+b_{2}(v,\delta_{2})+b_{1}(v,\delta_{1}) \\ &=& \dfrac{1}{2} a_{0}(v,v)-(f,v)_{X}+b(v,\delta), \end{array}\)\\ \(\mathcal{L}(.,.)\) has at least one solution, see [10], in fact, from \(\mathcal{L}(v,0)=\dfrac{1}{2}a_{0}(v,v)-(f,v)_{X}\) and the coercivity of \(a_{0}(.,.)\) we have $$\lim_{||v||_{X}\rightarrow +\infty}\mathcal{L}(v,0)=+\infty .$$ Moreover
Step 2.
Assume now that \(f \in X\), there exists a unique solution \((u,\lambda) \in X \times M\) of the Problem 4, when we have two solutions \((u_{1},\lambda)\) and \((u_{2},\gamma)\) of Problem 4 corresponding to two given data \(f_{1}\in X \times X\) and \(f_{2}\in X \times X\) respectively, then
Let \(\tau \in [0,1]\). Assume for given \(f,g \in X\) there exists a unique solution of Problem 4 with \(t=\tau\), \((u,\lambda)\in X \times M\). Then for given \(f\in X\) there exists a unique solution \((u,\lambda)\in X\times M\) of Problem 4 with \(t\in [\tau;\tau+t_{0}]\subset [0,1]\), where: $$0< t_{0}< \dfrac{\alpha m_{a}}{M_{a}(\alpha+m_{a}+2M_{a})}< 1.$$ Indeed, given \(f\in X\), we define the operator \(T:X \times M \longrightarrow X \times M\) as follows \(T(w,\xi):=(u,\lambda)\) if \((u,\lambda)\) is the solution of the following problem:
Problem 5. For given \(f\in X\), find \(u\in X\) and \(\lambda \in M\), such that
We substitute \(F_{s}\) in the first equation, we find \((\bar{u},\bar{\lambda})\) be the unique fixed point of \(T\), using the definition of the operator \(T\), we deduce that $$a_{\tau}(\bar{u},v)+(s-\tau)c(\bar{u} ,v)+b(v,\bar{\lambda})=(f,v)_{X},\hspace{1cm}\forall\;\; v\in X,$$ $$b_{1}(\bar{u},\delta- \bar{\lambda}_N) \leq 0,\hspace{1cm}\forall\;\; \delta\in M_N,$$ $$b_{2}(\bar{u},\delta-\bar{\lambda}_N) \leq 0,\hspace{1cm}\forall\;\; \delta\in M_T,$$ that is $$a_{0}( \bar{u},v)+sc(\bar{u},v)+b(v,\bar{\lambda})=a_{s}(\bar{u},v)+b(v,\bar{\lambda} )=(f,v)_{X},\hspace{1cm}\forall\;\; v\in X,$$ $$b_{1}(\bar{u}, \delta- \bar{\lambda}_N)\leq 0,\hspace{1cm}\forall\;\; \delta\in M_N,$$ $$b_{2}(\bar{u} ,\delta- \bar{\lambda}_T )\leq 0,\hspace{1cm}\forall\;\; \delta\in M_T,$$ which gives the existence of solution. In order to justify the uniqueness, let us assume that the problem with \(l=s\in [\tau,\tau+t_{0}]\) has two solutions \((u_{1},\lambda)\) and \((u_{2},\gamma)\), we have \begin{eqnarray*} a_{s}(u_{1}-u_{2},v)+b(v,\lambda-\gamma)&=&0\\ a_{s}(u_{1}-u_{2},u_{1}-u_{2})&=& b(u_{2}-u_{1},\lambda-\gamma)\\ &=& b_{1}(u_{2}-u_{1},\lambda_N-\beta_{1})+b_{2}(u_{2}-u_{1},\lambda_T-\gamma_{2})\leq 0, \end{eqnarray*} hence, by coercivity of \(a_{s}\), we get \(u_{1}=u_{2}\) and \(\lambda=\gamma\).
Step 4. Using Step 3, a finite number of times, we deduce that the Problem 4 admits a unique solution \((u,\lambda )\) for \(t=1\).
Step 5. In order to get (44), let us consider the data \(f_{1,2}\in X\) $$a(u_{1},v)+b(v,\lambda)=(f_{1},v)_{X},\hspace{1cm}\forall\;\; v \in X,$$ $$b_{1}(u_{1},\delta-\lambda_N)\leq 0,\hspace{1cm}\forall\;\; \delta\in M_N,$$ $$b_{2}(u_{1},\delta-\lambda_T)\leq 0,\hspace{1cm}\forall\;\; \delta\in M_T,$$ and $$a(u_{2},v)+b(v,\gamma)=(f_{2},v)_{X},\hspace{1cm}\forall\;\; v \in X,$$ $$b_{1}(u_{2},\delta-\gamma_{1})\leq 0,\hspace{1cm}\forall\;\; \delta\in M_N,$$ $$b_{2}(u_{2},\delta-\gamma_{2})\leq 0,\hspace{1cm}\forall\;\; \delta\in M_T.$$ By subtracting this two equations, we find $$a(u_{1}-u_{2},v)+b(v,\lambda)-b(v,\gamma)=(f_{1}-f_{2},v)_{X}.$$ For \(v=u_{1}-u_{2}\), we have $$a(u_{1}-u_{2},u_{1}-u_{2})+b(u_{1}-u_{2},\lambda)-b(u_{1}-u_{2},\gamma)=(f_{1}-f_{2},u_{1}-u_{2})_{X},$$ which implies that \begin{eqnarray*} a(u_{1}-u_{2},u_{1}-u_{2})&=&b(u_{1}-u_{2},\gamma)-b(u_{1}-u_{2},\lambda)+(f_{1}-f_{2},u_{1}-u_{2})_{X}\\ &\leq& b_{2}(u_{1}-u_{2},\gamma_{2}-\lambda_T)+(f_{1}-f_{2},u_{1}-u_{2})_{X}\\ m_{a}||u_{1}-u_{2}||^{2}_{X}&\leq& ||f_{1}-f_{2}||_{X}||u_{1}-u_{2}||_{X},\end{eqnarray*} that is
[Proof of Theorem 1
We consider \(X=\tilde{V}\), \(Y=H_\Gamma^{*}\) and \(M_N \times M_N \) given by (18). The subset \(M_N \times M_N\) is a non-empty, closed, convex of \(H_\Gamma^{*} \times H_\Gamma^{*}\) and \(0_{H_\Gamma^{*}} \in M\).
By using (12) and (15) we deduce that there exists \(M_{a} =M_{a}(\mathcal{A},\mathcal{E},\beta)>0\) and \(m_{a} =m_{a}(\mathcal{A},\beta)>0\) such that the bilinear form \(a(.,.)\) satisfies
$$
| a(\tilde{u},\tilde{v})| \leq M_{a} \| \tilde{u}\|_{V}\| \tilde{v}\|_{\tilde{V}},\;\; \forall\;\; \tilde{u},\tilde{v} \in V,
$$
%%
$$
a(\tilde{u},\tilde{u}) \geq m_{a} \| \tilde{u}\|_{V}^{2}, \;\; \forall\;\; \tilde{u} \in V.
$$
By the conditions (21) and (22) we deduce that the bilinear form \(b(.,.)\) satisfies (32).
Using inf-sup property (34) and Theorem \ref{2} we find the result of Theorem 1.
Proof of Proposition 1 To prove the convergence result 1 of the Algorithm 1, lets reconsider the following perturbed problem, for \(l\in [\tau;\tau+t_{0}]\subset [0,1]\), where this time:
Problem 6. (Fixed point problem) For given \(f,g\in X\), find \(u\in X\) and \(\lambda \in M\), such that
Problem 7. For given \(f\in X\), find \(u^{\ell+1}\in X\) and \(\lambda^{\ell+1} \in M\), such that
4. Discretization and numerics
The problem is now how to identify the multipliers \(\lambda_N\) and \(\lambda_T\) in the convex sets \(M_{1,2}\). One manner to do this, is the use of Projection maps. To this end, we consider the finite dimensional spaces \(V^{h}\subset V\), \(K^{h} = K \cap V^{h}\) and \(W^{h}\subset W\) approximating the spaces \(V\) and \(W\), respectively, in which \(h>0\) denotes the spatial discretization parameter. Let us define: $$ X_{n}^{h}=\left\lbrace v_{n| \Gamma_3}^{h}:v^{h}\in V^{h} \right\rbrace , \; X_{T}^{h}=\left\lbrace v_{\tau | \Gamma_3}^{h}:v^{h}\in V^{h} \right\rbrace , $$ and $$ X^{h}=\left\lbrace v_{|\Gamma_3}^{h}:v^{h}\in V^{h} \right\rbrace = X_{n}^{h}\times X_T^{h}. $$ Let us denote also \(X^{* h}_{n} \subset X^{*}_{n} \bigcap L^{2}(\Gamma_3)\) and \(X^{*h}_{T} \subset X^{*}_{T} \bigcap L^{2}(\Gamma_3;\mathbb{R}^{d-1})\) the finite discretizations of \(X^{*}_{n}\) and \(X^{*}_{T}\) respectively, such that the following discrete Babuska-Brezzi inf-sup conditions hold; $$ \inf_{\lambda^{h}_{T}\in X^{*h}_{T}} \sup_{v^{h}\in V^{h}}\dfrac{\left\langle \lambda^{h}_{T},v^{h}_\tau \right\rangle }{\| v^{h} \|_{V} \| \lambda^{h}_{T} \|_{X^{*h}_{T}} }\geq \alpha >0,\; \inf_{\lambda^{h}_{N}\in X^{*h}_{n}} \sup_{v^{h}\in V^{h}}\dfrac{\left\langle \lambda^{h}_{N},v^{h}_{n} \right\rangle }{\| v^{h} \|_{V} \| \lambda^{h}_{N} \|_{X^{*h}_{n}} }\geq \alpha >0, $$ with \(\alpha\) independent of \(h\). We consider the following discrete approximation of Problem 2:Problem 8. Find \(\tilde{u}^{h}\in\tilde{V}^{h}\) and \(\lambda^{h}=(\lambda_{N}^{h},\lambda_{T}^{h})\in M_N^{h}\times M_T^{h}(\mu\lambda_N^h)\) such that: $$\left\lbrace \begin{array}{c} a(\tilde{u}^{h},\tilde{v}^{h})+b_{1}(\tilde{v}^{h},\lambda_N^{h})+b_{2}(\tilde{v}^{h},\lambda_T^{h})=(f^{h},\tilde{v}^{h})_{\tilde{V}},\;\; \forall\;\; \tilde{v}^{h}\in\tilde{V}^{h},\\ \lambda_N^{h}=P_{M_{N}^{h}}\left( \lambda_N^{h}-ru^{h}_{n} \right),\\ \lambda_T^{h}=P_{M_{T}^{h}(\mu\lambda_N^h)}\left( \lambda_T^{h}-ru^{h}_\tau \right), \end{array}\right. $$ where \(r>0\) and $$ M_{T}^{h}(\mu\lambda_N^h)=\left\lbrace \delta^{h} \in X^{* h}_{T},\hspace{1cm}\langle \delta^{h} ,v^{h} \rangle_{\Gamma_{3}}\leq\int_{\Gamma_{3}}\mu\lambda_N^h|v_\tau^{h}| d \Gamma,\;v^{h}\in H_\Gamma \right\rbrace , $$ $$ M_{N}^{h} = \left \lbrace \delta^{h} \in X^{* h}_{n},\hspace{1cm}\langle \delta^{h} ,v^{h} \rangle_{\Gamma_{3}}\leq 0,\;v^{h}\in K^{h}_n \right\rbrace , $$ and where \(P_{M}\) is the projection over \(M\). For more details we refer to [27].
4.1. Matrix formulation
In this section, we adopt the same technical discretization as in the work [27]. Let \(\textbf{a}_j\) (\(j=1,\ldots,n_c\)) be a contact node (i.e. \(\textbf{a}_j\) are the nodes forming \(\Gamma_3\)). The displacement vector at \(\textbf{a}_j\) is denoted by \(\textbf{u}_j\), i.e. \(\textbf{u}_j=u(\textbf{a}_j)\). Denoting \(\textbf{n}_j\) and \(\textbf{t}_j\), the unit outward normal vector to \(\Gamma_3\) and the unit tangential vector to \(\Gamma_3\), respectively. Let us introduce the linear mappings- \(\textbf{N} \,:\,\mathbb{R}^{2d}\rightarrow\mathbb{R}^{n_c}\), such that \((\textbf{N}\textbf{u})_j=\textbf{u}_j^\top \textbf{n}_j\), \(j=1,\ldots,n_c\).
- \(\textbf{T}\,:\,\mathbb{R}^{2d}\rightarrow\mathbb{R}^{n_c}\), such that \((\textbf{T}\textbf{u})_j=\textbf{u}_j-(\textbf{u}_j^\top \textbf{n}_j)\textbf{n}_j=(\mathbb{I}_d-\textbf{n}_j\textbf{n}_j^\top)\textbf{u}_j\), \(j=1,\ldots,n_c\).
- \(\textbf{A}\), \((2d)\times (2d)\) the elastic matrix (symmetric and positive definite) ;
- \(\textbf{B}\), \(d \times d\) electric potential stiffness matrix (symmetric positive definite);
- \(\textbf{E}\), \(d \times (2d)\) coupling matrix;
- \(\textbf{M}_{n}\) and \( \textbf{M}_\tau\) normal and tangential mass matrices (\(n_c\times n_c\));
- \( \textbf{f}\) (the external forces in \(\mathbb{R}^{2d}\)), \(\textbf{q}\) (the external charges in \(\mathbb{R}^{d}\)).
- \(\lambda_{N}\), \(\lambda_{T}\) the vectors associated to \(\lambda_N^h\) and \(\lambda_T^h\) respectively.
Remark 1. In practice, the Algorithm 2 is solved using Tresca friction with slip bound \(S^\ell\) and an fixed point iteration is used to compute the problem with Coulomb friction, i.e. \(S^{\ell+1}=-\mathcal{F}\lambda_N^{\ell}\).
To compute the solution of the system (70), we proceed by the following elimination technique:4.2. Numerical example
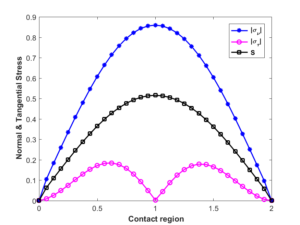
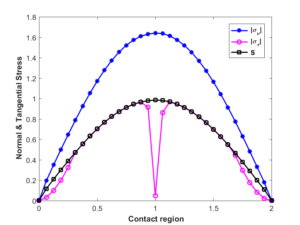
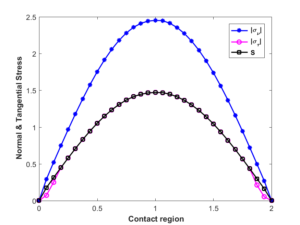
The algorithms are implemented in MATLAB on computer equipped running Windows 10 core i7 of 2.4GHz clock frequency and 6 GB RAM. As example, the domain consists of two-dimensional rectangular domain \(\Omega=(0,\;2)\times (0,\;1)\) as in the Figure 1, with boundaries \(\Gamma_D =\{0\}\times \left[0,\;1\right]\cup \{2\}\times \left[0,\;1\right]\), \(\Gamma_3 = \left[0,\;2\right]\times \{0\}\) and \(\Gamma_N =\left[0,\;2\right]\times \{1\}\). External body force and charge are \(f=0\) and \(q=0\), respectively. On \(\Gamma_D\) the displacements and the electric potential are prescribed, i.e., \(\textbf{u}=0\) and \(\varphi=0\) on \(\Gamma_D\). On \(\Gamma_N\), non-homogeneous Neumann boundary conditions are prescribed \(f_0=\sigma (u).n=-2\). On \(\{1\}\times(0,\;1)\) the homogeneous Neumann boundary condition is applied (\(\sigma n=0\) and \(Dn=0\)). For seek of simplicity, the normalized gap between \(\Gamma_3\) and the foundation is \(g(\mathbf x)=0\) and the friction coefficient is \(\mathcal{F}=0.6\). The mesh is generated by using Matlab function "kmg.m" built by the author in [29].The deformed configuration is showed in the Figure 2 and the the contour plot of the electric potential distribution are showed in the Figure 3. The Figure 4 show the Lagrange multipliers \(\lambda_{T,N}\) in the contact zone \(\Gamma_3\) corresponding to the problem with Coulomb friction condition. The Figures 5 and 6 show the Lagrange multipliers \(\lambda_{T,N}\) with different choices of loads acting on \(\Gamma_2\), it is clear that the slide occurs when the load is important (large enough). The performance of the algorithm is presented in the Table 1, as showed the number of iterations is independent of mesh refinement and the time of execution is significant.
Figure 1. Initial configuration.
Figure 2. Deformed configuration.
Figure 3. Multipliers for \(\mathcal{F}=0.6\).
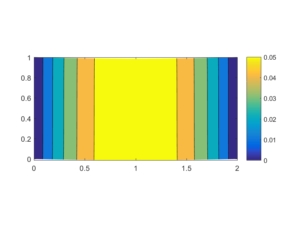
Figure 4. Contour plot of electic potential.
Figure 5. Multipliers with load \(-4\).
Figure 6. Multipliers with load \(-6\).
Table 1. Performance of the algorithms.
| Mesh size \(h\) | 1/32 | 1/64 | 1/128 | 1/256 |
|---|---|---|---|---|
| Number of iterations of FP | 3 | 4 | 4 | 4 |
| Number of iterations of UA | 39 | 39 | 39 | 39 |
| Number of iterations of PCG | 2 | 2 | 2 | 2 |
| CPU time (seconds) | 0.1341 | 2.0863 | 21.1882 | 238.4585 |
5. Conclusion
We have investigated numerical analysis of a model describing the process of contact between a piezoelectric body and non-conductive foundation. The behavior of the material is modeled with a electro-elastic constitutive law. The contact is formulated by Signorini conditions and Coulomb friction. In coming works, more general problem with non linear constitutive equation and non monotone friction will be treated. This is may be handled by fixed point iteration and hemivariational inequalities [30]migorski2012nonlinear}.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Competing Interests
The author(s) do not have any competing interests in the manuscript.References
- Arnau, A., & Soares, D. (2009). Fundamentals of piezoelectricity. In Piezoelectric transducers and applications (pp. 1-38). Springer, Berlin, Heidelberg.[Google Scholor]
- Katzir, S. (2006). The discovery of the piezoelectric effect. In the beginnings of piezoelectricity (pp. 15-64). Springer, Dordrecht.[Google Scholor]
- Bisegna, P., Maceri, F., & Lebon, F. (2002). The unilateral frictional contact of a piezoelectric body with a rigid support. In Contact mechanics (pp. 347-354). Springer, Dordrecht.[Google Scholor]
- Taik, A., Essoufi, E., Benkhira, E., & Fakhar, R. (2010). Analysis and numerical approximation of an electro-elastic frictional contact problem. Mathematical Modelling of Natural Phenomena, 5 (7), 84-90.[Google Scholor]
- Shillor, M., Sofonea, M., & Telega, J. J. (2004). Models and analysis of quasistatic contact: variational methods (Vol. 655). Springer Science & Business Media. [Google Scholor]
- Sofonea, M., & Essoufi, E. H. (2004). A piezoelectric contact problem with slip dependent coefficient of friction. Mathematical Modelling and Analysis, 9 (3), 229-242. [Google Scholor]
- Sofonea, M., & Matei, A. (2012). Mathematical models in contact mechanics (No. 398). Cambridge University Press.[Google Scholor]
- Barboteu, M., Fernández, J. R., & Ouafik, Y. (2008). Numerical analysis of two frictionless elastic-piezoelectric contact problems. Journal of mathematical analysis and applications, 339 (2), 905-917.[Google Scholor]
- Kikuchi, N., & Oden, J. T. (1988). Contact problems in elasticity: a study of variational inequalities and finite element methods (Vol. 8). Siam.[Google Scholor]
- Ekeland, I., & Temam, R. (1999). Convex analysis and variational problems (Vol. 28). Siam.[Google Scholor]
- Fortin, M., & Glowinski, R. (2000). Augmented Lagrangian methods: applications to the numerical solution of boundary-value problems. Elsevier.[Google Scholor]
- Glowinski, R., & Le Tallec, P. (1989). Augmented Lagrangian and operator-splitting methods in nonlinear mechanics (Vol. 9). SIAM.[Google Scholor]
- Glowinski, R., & Marroco, A. (1975). Sur l'approximation, par éléments finis d'ordre un, et la résolution, par pénalisation-dualité d'une classe de problèmes de Dirichlet non linéaires. ESAIM: Mathematical Modelling and Numerical Analysis-Modélisation Mathématique et Analyse Numérique, 9 (R2), 41-76.[Google Scholor]
- Stadler, G. (2004). Semismooth Newton and augmented Lagrangian methods for a simplified friction problem. SIAM Journal on Optimization, 15 (1), 39-62.[Google Scholor]
- Essoufi, E. H., Fakhar, R., & Koko, J. (2015). A decomposition method for a unilateral contact problem with Tresca friction arising in electro-elastostatics. Numerical Functional Analysis and Optimization, 36 (12), 1533-1558.[Google Scholor]
- Essoufi, E. H., Koko, J., & Zafrar, A. (2017). Alternating direction method of multiplier for a unilateral contact problem in electro-elastostatics. Computers & Mathematics with Applications, 73 (8), 1789-1802.[Google Scholor]
- Hüeber, S., Matei, A., & Wohlmuth, B. I. (2005). A mixed variational formulation and an optimal a priori error estimate for a frictional contact problem in elasto-piezoelectricity. Bulletin mathématique de la Société des Sciences Mathématiques de Roumanie , 209-232.[Google Scholor]
- Matei, A. (2009). A Variational Approach for an Electro-Elastic Unilateral Contact Problem. Mathematical Modelling and Analysis, 14 (3), 323-334.[Google Scholor]
- Matei, A., & Sofonea, M. (2017). A mixed variational formulation for a piezoelectric frictional contact problem. IMA Journal of Applied Mathematics, 82 (2), 334-354.[Google Scholor]
- Haslinger, J., & Sassi, T. (2004). Mixed finite element approximation of 3D contact problems with given friction: error analysis and numerical realization. ESAIM: Mathematical Modelling and Numerical Analysis, 38(3), 563-578.[Google Scholor]
- Mandel, J. (1990). On block diagonal and Schur complement preconditioning. Numerische Mathematik, 58 (1), 79-93.[Google Scholor]
- Brezzi, F., & Fortin, M. (2012). \emph{Mixed and hybrid finite element methods} (Vol. 15). Springer Science & Business Media.[Google Scholor]
- Duvant, G., & Lions, J. L. (2012). Inequalities in mechanics and physics (Vol. 219). Springer Science & Business Media.[Google Scholor]
- Rabel, R. G., Han, W., & Sofonea, M. (2002). Quasistatic contact problems in viscoelasticity and viscoplasticity . American Mathematical Soc..[Google Scholor]
- Kinderlehrer, D., & Stampacchia, G. (1980). An introduction to variational inequalities and their application (Vol. 31). Siam.[Google Scholor]
- Voigt, W. (1928). Lehrbuch der kristallphysik (Vol. 962). Leipzig: Teubner.[Google Scholor]
- Khenous, H. B., Pommier, J., & Renard, Y. (2004). Hybrid discretization of the Signorini problem with Coulomb friction. \emph{Theoretical aspects and comparison of some numerical solvers. A paraître Numerical Applied Mathematics. [Google Scholor]
- Laborde, P., & Renard, Y. (2008). Fixed point strategies for elastostatic frictional contact problems. Mathematical methods in the applied sciences, 31 (4), 415-441.[Google Scholor]
- Koko, J. (2015). A Matlab mesh generator for the two-dimensional finite element method. Applied Mathematics and Computation, 250 , 650-664.[Google Scholor]
- Migórski, S., Ochal, A., & Sofonea, M. (2012). Nonlinear inclusions and hemivariational inequalities: models and analysis of contact problems (Vol. 26). Springer Science & Business Media.[Google Scholor]