Open Journal of Mathematical Analysis
ISSN: 2616-8111 (Online) 2616-8103 (Print)
DOI: 10.30538/psrp-oma2020.0053
Mathematical model for measles disease with control on the susceptible and exposed compartments
Department of Mathematical Sciences, African Institute for Mathematical Sciences, Senegal.; (S.O.S)
Department of Mathematical Sciences, Baze University, Nigeria.; (A.I & A.O.L)
Department of Mathematical Sciences, Universite Gaston Berger, Senegal.; (D.S)
\(^1\)Corresponding Author: oladimeji.s.sowole@aims-senegal.org
Abstract
Keywords:
1. Introduction
Measles disease has been recognized as one of the world's most contagious diseases, which has the potential to be extremely severe. The transmission mode of measles disease is by person-to-person through the air by infectious droplets which has over \(90\%\) attack rates among its susceptible persons [1]. Measles disease is caused by the measles virus, an infectious agent belonging to the virus family called Paramyxoviridae that causes an infection of the respiratory system with a common symptom of red rash on the infected person's skin [2]. Infectious diseases have been a serious concern for both human and animals populations globally. Control and prevention measures are therefore important tasks both from the human survival and economic point of views because public health issue is a major concern to the world. For effective intervention measures, a complete understanding of disease transmission like measles, and how burden they can be to a human, is therefore necessary. Even though the disease is possible and entirely preventable by taking two doses of a safe and effective vaccine, world-wide vaccination coverage with the first dose of measles vaccine still stands at \(85\%\) presently. This is still not close to the \(95\%\) proposed by World Health Organization (WHO) that will be needed to prevent outbreaks. Consequently, many people in some communities are still at risk of contracting the disease. According to WHO, the second dose of vaccination coverage, though increasing, still stands at \(67\%\) currently. But to be in a higher level of safety of not contracting the disease, the first and second doses of the vaccine must be taken.
Several factors are responsible for people not to be vaccinated against the disease. The wrong perceptions about immunization have caused some not to go for vaccination and release their wards for immunization [3]. Lack of access to health care facilities is another major factor, particularly among the rural people, and can cause them to mix out on vaccination programmes being organized by their governments.
Researchers have attributed the main causes of transmission to inappropriate education about the measles disease and low detection rate at early stages. Financial constrains is also a major factor as some individual will opt for treatment of the disease locally or traditionally than going to hospitals for professional treatments. Though there are campaigns coupled with regular and targeted measles vaccination coverage across the 36 states and Federal Capital Territory (FCT) in Nigeria, measles disease is still very prevalence with evidence of sickness and death from measles outbreaks. There is a measles outbreak in Nigeria during the first quarter of 2019. With almost six thousands cases of measles which nearly doubled the cases reported in 2018, and 15 deaths recorded as at March 2019 [4]. Evidently, measles disease is one of the infectious diseases invading Nigeria, so also some other developing countries in Africa.
Mathematical modelling of infectious diseases has proven to be powerful and useful tools. They are good in proposing and testing theories, and in comparing, planning, implementing and evaluating various detection, prevention, therapy and control intervention programs for infectious diseases. Right from the beginning of \(20^{th}\) century, researchers have been using epidemiological models to modelled infectious diseases [5]. Examples of such models are seen in [6, 7, 8]. Only a few of these models described by [5] focused on modelling childhood epidemics as measles. Roberts [9] carried out a study on predicting and preventing measles disease epidemics in New Zealand. In the work, they used a compartmental SIR model to model the dynamics of measles disease under varied immunization strategies in a population taking into consideration size and age structure. Momoh [10] developed a mathematical epidemiological model for control of measles disease. They used compartmental SEIR model for varying population size which best describes a population dynamics of developing countries like Africa. From previous literature, it has been ascertained that vaccination protects susceptibles individuals against infectious diseases such as measles by producing herd (crowd) immunity. Examples of such works can be found in [8, 11, 12, 13, 14] for instances. Sowole et al., [15], modelled measles disease using SEIR model. Taking Senegal as a case study, they looked at the effect a control measure will have on the exposed class over the entire population dynamics. Their model realized that if more people at the latent period go for treatment and therapy before they can be able to transmit the disease, the disease will be eradicated within a short period of time.
Our goal is to model measles disease transmission in Nigeria and come up with the control measures in reduction (and by extension, elimination) of the transmission of the disease in the country with control in the Susceptibles and Exposed compartments. Finding a threshold condition that will determine whether an infectious disease in a population will continue to spread or will die out with time in a given population is one of the fundamental questions of epidemiological modelling. So, we derived a fundamental epidemiological quantity, \(R_0\), called the basic reproductive number, which is the threshold parameter. This work uses a compartmental Susceptible-Exposed-Infective-Recovered epidemic model to formulate mathematical measles disease model and its corresponding mathematical analysis and numerical simulations were well presented.
The rest of the paper is structured as follow: the model is described and formulated in Section 2, model simulation is given in Section 3 and the conclusions are given in Section 4.2. Model description and formulation
The model divides the total human population at any given time into four sub-populations to explains the transmission dynamics of the measles disease in a given human population at a given time.
The total human population \(N(t)\) is divided into sub-populations of Susceptible class\(S(t)\), Exposed compartment \(E (t)\), Infective compartment \(I(t)\) and Recovered class \(R(t)\). So we have:
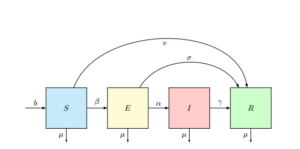
Figure 1. Flow Diagram of Measles Disease in a Deterministic Population.
Table 1. State variables used and their meanings.
| Variable | Meaning |
|---|---|
| \(S(t)\) | The number of susceptible individuals at a given time, t |
| \(E(t)\) | The number of exposed individuals at a given time, t |
| \(I(t)\) | The number of infective individuals at a given time, t |
| \(R(t)\) | The number of recovered individuals at a given time, t |
Susceptible compartment includes individuals who are at risk of developing measles infection if they had contact with infected individuals. Exposed class consists of individuals that had the infection but are not showing the symptoms of the measles disease and could not transmit the disease to others. Infective compartment consists of individuals that are showing the symptoms of the disease and can infect others.
The recovered human compartment comprises of individuals who have recovered from the disease and had permanent immunity.
The susceptible class \(S\) is increasing by recruitment (birth and/or immigration rate) which we denoted by \(b\). It is decreasing by susceptible class who have been immunized by the rate \(v\), is decreasing by infection if there is a contact with infected individuals at a rate of \(\beta\), and is diminishing by leaving (normal death and emigration) rate which we denoted by \(\mu\) so that:
Table 2. State parameters and their meaning.
| Parameter | Meaning |
|---|---|
| \(b\) | Recruitment rate ( by birth and/or immigrants) |
| \(v\) | vaccination rate for the susceptible class who later got vaccinated |
| \(\mu\) | Leaving rate (by death and/or emigrants) |
| \(\beta\) | The contact rate |
| \(\gamma\) | The rate at which an infective individuals recovered per unit time |
| \(\sigma\) | The rate of exposed individuals who have undergone testing and therapy |
| \(\alpha\) | The rate at which an exposed become infective |
The class \(E\) is decreasing by individuals who have undergone testing and measles therapy at a rate of \(\sigma\), the individuals who progresses into infected class at a rate of \(\alpha\) and also this class is diminishing by leaving rate of \(\mu\) so that:
2.1. Model assumptions
The following are the assumptions for the compartmental SEIR model for measles disease which we modeled in this work:- (i) The recruitment rate (which is through newborns and/or migrants) are assumed to be susceptible to the disease.
- (ii) We assumed that every person in the population under consideration is susceptible to the measles disease.
- (iii) Every Individual is equally likely to be infected by the infectious individual (s) in a case of contact except for those who are immune against the measles disease.
- (iv) Infectious individuals are detected early and isolated for immediate treatment and education
- (v) The population is homogeneously mixed. By homogeneously mixed we mean a population that interacts among themselves in such a uniformly manner.
- (vi) The population is a varying population where recruitment rate and leaving rate are differ within a given time steps.
- (vii) There is no treatment failure, a patient will either recover or die.
- (viii) Recovered individuals are permanently immune against the disease.
2.2. Properties of the model
The basic properties of our model are that of the properties of ``feasible solution'' and ``positivity of the solution''. The feasible solution of the model equations shows the region in which the solution of the equations are biologically significant and the positivity of the solutions tells the non-negativity of the solutions of the model equations.2.3. Feasible solution
Here, the deterministic SEIR model is used to model infectious disease in a human population. It will be reasonable to assumed that the parameters used and variables in all classes are non negative, that is \(t \geq 0\). The show that all variables of the model are non-negative for all given non-negative initial conditions are provided below. The feasible solution region which is positively invariant set of the model is given by:Lemma 1. The set \(\Omega\) is positively invariant and attracts all solution in \(\mathbb{R}_{+}^{4}\).
Proof. Since \(N(t) = S(t) + E(t) + I(t) + R(t)\). Adding Equations (2) to (5) together gives us the rate of change of the total population: \begin{align*} \frac{dN}{dt} &= \frac{dS}{dt} + \frac{dE}{dt} + \frac{dI}{dt} + \frac{dR}{dt} \\ &= b - \mu(S+E+I+R)\\ &= b - \mu N \hspace{1cm} (since \hspace{0.1cm} N \hspace{0.1cm} = S+E+I+R).\end{align*} This is a first order linear differential equation and a first order linear differential equation of the form
2.3.1 Positivity of results
In this section we prove that all variables in the SEIR model Equations (2) to (5) are non-negative.Lemma 2. Let the initial data set be \((S, E, I, R) (0) \geq 0 \in \Omega\), then the solution set \((S(t), E(t), I(t), R(t) ) \) of the equations (2) to (5) is positive \(\forall\]t > 0\).
Proof. From Equation (2) if we assumed that: \[\frac{dS}{dt} = b - \beta SI - (v + \mu) S \geq -(\beta SI + v + \mu S ).\] That is \[\frac{dS}{dt} \geq -(\beta I + v + \mu )S \hspace{0.5cm} or \hspace{0.5cm} \frac{dS}{S} \geq -(\beta I + v + \mu )dt \hspace{1cm} (by \hspace{0.1cm} separation \hspace{0.1cm} of \hspace{0.1cm} variables, \hspace{0.1cm} since \hspace{0.1cm} S \ne 0) .\] Integrating both sides of the inequalities, we have \[In \big( S(t) \big) \geq -(\beta I + v + \mu )t + K.\] So that \[S(t) \geq K \exp \bigg( -(\beta I + v + \mu )t\bigg). \] At \(t = 0\); this becomes: \[S(t) \geq S(0) \exp \bigg( -(\beta I + v + \mu )0\bigg) \geq 0 \hspace{1cm} (since \hspace{0.1cm} (\beta I + v + \mu ) > 0).\] That is \[ S(t) > 0.\] Similarly from Equation (3), we have \[\frac{dE}{dt} = \beta SI - (\mu + \alpha + \sigma)E \geq - (\mu + \alpha + \sigma)E \] i.e., \[\frac{dE}{dt} \geq - (\mu + \alpha + \sigma)E \] or \[\frac{dE}{E} \geq - (\mu + \alpha + \sigma)dt \hspace{1cm} (by \hspace{0.1cm} separation \hspace{0.1cm} of \hspace{0.1cm} variables, \hspace{0.1cm} since \hspace{0.1cm} E \ne 0) .\] Integrating both sides of the inequalities we have; \[ E(t) \geq K \exp \bigg(- (\mu + \alpha + \sigma)t \bigg).\] At \(t = 0\), we have that \[E(t) \geq E(0) \exp \bigg(- (\mu + \alpha + \sigma\bigg)0 \geq 0, \hspace{1cm} (since \hspace{0.1cm} (\mu + \alpha + \sigma) > 0.\] That is \( E(t) > 0.\) Also from Equation (4), we have \[\frac{dI}{dt} = \alpha E - (\mu + \gamma)I \geq - (\mu + \gamma)I.\] That is \[\frac{dI}{dt} \geq - (\mu + \gamma)I.\] Then we have that: \[\frac{dI}{I} \geq - (\mu + \gamma)dt.\] On integrating we obtains \[ In \big( I(t) \big) \geq - (\mu + \gamma)t + K,\] that is \[I(t) \geq K \exp \bigg(- (\mu + \gamma)t \bigg).\] At \(t=0\), we have \(I(t) \geq I(t) \exp \bigg(- (\mu + \gamma)0 \bigg).\) So that \( I(t) > 0.\) Finally from Equation (5), we have \[\frac{dR}{dt} = v S + \gamma I + \sigma E - \mu R > \sigma E - \mu R.\] That is, \[\frac{dR}{dt} > \sigma E - \mu R.\] Which has an integrating factor \( I.F = \exp (-\mu t).\) Then we have: \[\frac{dR}{dt}.\exp (-\mu t) > \sigma E. \exp (-\mu t) - \mu R . \exp (-\mu t).\] Integrating at constant \(K\), we have \[ R(t) > \frac{\sigma E}{\mu} + K \exp (-\mu t).\] When \(t=0\) we obtained that \(R(0) >\frac{\sigma E}{\mu} + K.\) The solution then becomes \[R(t) > R(0)\exp (-\mu t) +\frac{\sigma E}{\mu} (1- \exp (-\mu t)).\] That is \(R(t) > 0.\) Hence, we have proved that all variables are positive \(\forall t > 0\).
2.4. Existence and uniqueness of solution for the SEIR model
The general first-order ODE is in the form:- (1) Under what conditions, the solution to Equation (10) exists?
- (2) Under what conditions, there is a unique solution to Equation (10)?
Theorem 1.[Uniqueness of Solution] Suppose \(D\) denotes the domain, and
Lemma 3. If \(f (t, x)\) has continuous partial derivative \(\frac{\partial{f_i}}{\partial{x_j}}\) on a bounded closed convex domain \(\mathbb{R}\) (i.e, convex set of real numbers), where \(\mathbb{R}\) is used to denotes real numbers, then it satisfies a Lipschitz condition in \(\mathbb{R}\).
Our interest is in the domainTheorem [Existence of solution] Let \(D\) denote the domain defined in (11) such that (12) and (13) hold. Then, there exist a solution of model system of Equations (2)-(5) which is bounded in the domain \(D\).
Proof. Let
2.5. Existence of steady states of the system
Under this section we will find the equilibrium points and established asymptotic stability of the SEIR model. In order to obtained the equilibrium points of the system, we equate the system of equations of the model to zeros; i.e.;2.6. Stability of the SEIR model (local asymptotic stability)
To find the local stability of the model, we first find the equilibrium points (disease free equilibrium) of the system (2) to (5). By equating the system to zeros we haveNote 1. We assumed \(b \ne \mu\) for this model.
2.7. The basic reproduction number \(R_0\)
The basic reproduction number \(R_0\) of an infection can be thought of as the number of cases one measles infection case can generates on average over the course of its infectious period, in an otherwise uninfected (susceptible) population\footnote{Source: Wikipedia}.
We determined the basic reproduction number \(R_0\) by employing the method of next generation matrix. We considered only the two infected classes in our model; the Exposed \(E\) and the Infectious \(I\) compartments. That is \(m = 2\). Define \(G = F V^{-1}\), therefore \(R_0 = \rho (F V^{-1})\) where \(\rho (F V^{-1})\) is called the spectral radius of \(FV^{-1}\). ({The spectral radius is the maximum of the absolute value of the eigenvalues}.)
Let \(H'(x) = \mathcal{F}(x) - \mathcal{V}(x),\) which givesLet's define \[ R_0 = \frac{b \beta \alpha}{\mu (\mu + \alpha +\sigma)(\mu + \gamma)} \hspace{0.3cm} \text{where:} \hspace{0.2cm} \mu (\mu + \alpha +\sigma)(\mu + \gamma) \ne 0\,.\]
2.8. Interpretation of \(R_0\)
\(R_0\) is used to explained the fact that the transmission rate, that is, the rate at which exposed individuals will become infected and the contact rate, i.e.; the average number of effective contacts with other (susceptible) individuals per infective individuals per unit time which is relative to the rate at which an infectious individuals will recovered per unit time plays a significant role in determining whether or not the measles epidemic will occur in a given human population. Thus, the disease free equilibrium \((\frac{b}{\mu}, 0, 0, 0)\) is locally asymptotically stable given that \(Ro < 1\), that is, \(b \beta \alpha < \mu (\mu + \alpha +\sigma)(\mu + \gamma). \) Alternatively, if \(Ro > 1\), then the disease free equilibrium is unstable, i.e., the system is said to be uniformly persistent, in other words the measles disease is endemic. Hence, \(R_0\) is a threshold parameter for the model that will determines the number of equilibria.2.9. Endemic Equilibrium
The next thing in our analysis is to shows that an endemic equilibrium:2.10. Local asymptotic stability
We established the local stability of the disease-free equilibrium using Jacobian matrix of Equations (2) to (5) and evaluate at disease free equilibrium \(\mathcal{P}_0\). We achieve this by evaluating the Jacobian matrix of Equations (2) to (5) at \(\mathcal{P}_0 = (\frac{b}{\mu}, 0, 0, 0)\). The local stability of the model is determined from the eigenvalues of the Jacobian matrix of the model equations at \(\mathcal{P}_0\). Thus, the Jacobian matrix of Equations (2) to (5) is given by2.11. Application of \(R_0\) to measles in Nigeria.
A deterministic compartmental mathematical model for measles has been formulated with the aim of the study of the effects of heterogeneous mixing, transmission and control (or elimination) of the disease in Nigeria. Moreover, the basic reproduction number, \(R_0\), has been derived, which is the threshold parameter. Recall thatTable 3. Model parameter values used and Sources.
| Parameter | Value | Source |
|---|---|---|
| \(b\) | 0.03691 | [17] and [18] |
| \(v\) | 0.0, 0.25, 0.50 \& 0.75 | Assumed |
| \(\mu\) | 0.01241 | [19] and [18] |
| \(\beta\) | 0.09091 per day | Immunization Action Coalition |
| \(\gamma\) | 0.125 per day | [20] |
| \(\sigma\) | 0.0, 0.25, 0.50 \& 0.75 | Assumed |
| \(\alpha\) | 0.14286 per day | [20] |
In summary, when \(\sigma = 0\) we have \(R_0 > 1\) and when \(\sigma \le 1\) we have \(R_0 < 1\). This illustrate the fact that \(\sigma\), which is the rate of exposed individuals who have undergone testing and therapy, will play a significant role in controlling (and eliminating) of the disease. Thus, the disease free equilibrium \((\frac{b}{\mu}, 0, 0, 0)\) is locally asymptotically stable when \(Ro < 1\) for \(\sigma \le 1\) , that is, \(b \beta \alpha < \mu (\mu + \alpha +\sigma)(\mu + \gamma). \) Alternatively, when \(\sigma = 0\), \(Ro > 1\), then the disease-free equilibrium is unstable, i.e., the measles disease will be endemic in the population. Hence, we have established the fact that \(R_0\) is a threshold parameter for the model that will determine the number of equilibria.
3. Numerical results
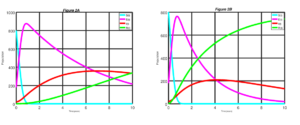
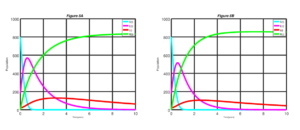
In this section, we consider the explicit fourth-order Runge-Kutta (RK4) scheme for solving numerically the non-linear first order ordinary differential equations (ODEs) of our SEIR model of Equations (6) with given initial conditions. Here, numerical simulations are used to show the impact of vaccination and therapy using the RK4 scheme on the state equations. Details of the RK4 are discussed in [15]. State equations are solved over a simulated period of time using the RK4 scheme. The parameters used in the simulation are in the Table 3. The simulation results are depicted in Figures 2 to 5.Figure 2. Measles dynamics is shown when \(\sigma\) = 0.0 and v = 0.0 (left) and when \(\sigma\) = 0.25 and v = 0.0 (right)
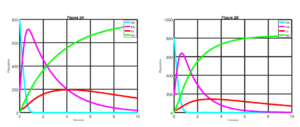
Figure 3. Measles dynamics is shown when \(\sigma\) = 0.25 and v = 25 (left) and when \(\sigma\) = 0.50 and v = 0.25 (right)
Figure 4. Measles dynamics is shown when \(\sigma\) = 0.50 and v = 0.50 (left) and when \(\sigma\) = 0.75 and v = 0.50 (right)
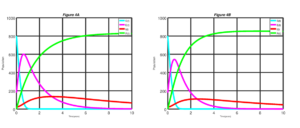
Figure 5. Measles dynamics is shown when \(\sigma\) = 0.50 and v = 0.75 (left) and when \(\sigma\) = 0.75 and v = 0.75 (right)
3. 1. Interpretation of Simulation Results
In Figure 2 we present the dynamics of measles disease when \(\sigma = 0.0\) and \(v = 0 \) and when \(\sigma = 0.25\) and \(v = 0\). We can see in the Figure 2 that, if none of the exposed individuals at the latent period are diagnosed and treated, and there is no control measure been introduced into the susceptible class. It will take a much longer time for exposed individuals to decrease. Likewise, it takes a significantly longer period before we notice any significant improvement for individuals to recovered from the measles disease. Similarly, infective individuals will significantly increase before noticing a drop in the number of infective individuals. On the order hand, when \(25\%\) of the exposed individuals at the latent period are diagnosed and treated, there is a clear improvement in the result.
In Figure 3, we do the simulation of the model when \(\sigma = 0.25\) and \(v = 25\) and when \(\sigma = 0.50\) and \(v = 0.25\). It can be observed from Figure 3 that if \(25\%\) of susceptible individuals are vaccinated in addition to increases of \(25\%\) to \(50\%\) of the exposed individuals at the latent period who are diagnosed and treated. It will take lesser time for exposed individuals to decrease significantly. Also, it takes a significant lesser period before noticing any significant improvement for individuals to recovered from the disease. Similarly, infective individuals will significantly decline over time.
Figure 4, above shows the dynamics of measles disease when \(\sigma = 0.50\) and \(v = 50\) and when \(\sigma = 0.75\) and \(v = 0.50\). From the simulation result of the Figure 4, if \(50\%\) of susceptible individuals are vaccinated in addition to increases of \(50\%\) to \(75\%\) of the exposed individuals at the latent period, who are diagnosed and treated,. There is a sudden decline of exposed individuals with time. This shows a significantly improved result in comparison with what we have in the two figures above. Also, it takes a significant much lesser period for individuals to recover from the disease. Similarly, infective individuals will significantly take a lesser period to go down over time.
Figure 5 shows the simulation of the model when \(\sigma = 0.50\) and \(v = 75\) and when \(\sigma = 0.75\) and \(v = 0.75\). Looking at the Figure 5 closely, we discovered that if \(75\%\) of exposed individuals at the latent period are diagnosed and treated. In addition to increases of \(50\%\) to \(75\%\) of susceptible individuals who are vaccinated, we have a better result in comparison to the previous three results stated above.
Conclusion
The SEIR model showed significant success in attempting to predict the causes of measles disease transmission within a given population. The model strongly indicated that the spread of disease largely depends on the contact rates of susceptible individuals with infected individuals within a population. With the assumed values for our state variables, we modelled a measles disease in Nigeria using deterministic SEIR model to investigate the impact the control measures can have on susceptibles, as well as exposed individuals at latent period, over the entire population dynamics in controlling and eliminating the disease. Consequently, we established the existence of a solution, uniqueness of the solution, and stability of the solution. The application of \(R_0\) to measles data of Nigeria was also given. Finally, numerical simulations of the model with the RK4 scheme was well presented.Acknowledgments
We appreciate the support given to us by African Institute for Mathematical Sciences (AIMS), Senegal. All the authors are well appreciated for their contributions.Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.Competing Interests
The author(s) do not have any competing interests in the manuscript.References
- Measles transmission mode. (October 2018). Retrieved from https://www.cdc.gov/measles/about/transmission. html.
- Measles disease and transmission mode. (September 2018). Retrieved from https://www.ncdc.gov.ng/diseases /info/M.
- Immunization Misconceptions. (September 2019). Retrieved from https://www.who.int/vaccine\_safety/initiative/ detection/immunization\_misconceptions/en/
- Measles Outbreak in Nigeria. (2019). Retrieved from https://reliefweb.int/report/nigeria/nigeria-measles-outbreak- dg-echo-who-ncdc-ngos-echo-daily-flash-16-march-2019.
- Hethcote, H. W. (2000). The mathematics of infectious diseases. SIAM review, 42(4), 599-653.[Google Scholor]
- Bakare, E. A., Adekunle, Y. A., & Kadiri, K. O. (2012). Modelling and Simulation of the Dynamics of the Transmission of Measles. International Jounal of Computer Trends and Technology, 3, 174-178.[Google Scholor]
- Bolarian, G. (2014). On the dynamical analysis of a new model for measles infection. International Journal of Mathematics Trends and Technology, 7(2), 144-155.[Google Scholor]
- Fred, M. O., Sigey, J. K., Okello, J. A., Okwoyo, J. M., & Kang'ethe, G. J. (2014). Mathematical modeling on the control of measles by vaccination: Case Study of KISII County, Kenya. The SIJ Transactions on Computer Science Engineering and Its Applications (CSEA), 2, 61-69.[Google Scholor]
- Roberts, M. G., & Tobias, M. I. (2000). Predicting and preventing measles epidemics in New Zealand: application of a mathematical model. Epidemiology & Infection, 124(2), 279-287.[Google Scholor]
- Momoh, A. A., Ibrahim, M. O., Uwanta, I. J., & Manga, S. B. (2013). Mathematical model for control of measles epidemiology. International Journal of Pure and Applied Mathematics, 87(5), 707-717.[Google Scholor]
- Tessa, O. M. (2006). Mathematical model for control of measles by vaccination. In Proceedings of Mali Symposium on Applied Sciences (Vol. 2006, pp. 31-36).[Google Scholor]
- Momoh, A. A., Ibrahim, M. O., Uwanta, I. J., & Manga, S. B. (2013). Mathematical model for control of measles epidemiology. International Journal of Pure and Applied Mathematics, 87(5), 707-717.[Google Scholor]
- Ochoche, J. M., & Gweryina, R. I. (2014). A mathematical model of measles with vaccination and two phases of infectiousness. IOSR Journal of Mathematics, 10(1), 95-105.[Google Scholor]
- Verguet, S., Johri, M., Morris, S. K., Gauvreau, C. L., Jha, P., & Jit, M. (2015). Controlling measles using supplemental immunization activities: a mathematical model to inform optimal policy. Vaccine, 33(10), 1291-1296.[Google Scholor]
- Sowole, S. O., Sangare, D., Ibrahim, A. A., & Paul, I. A. (2019). On the existence, uniqueness, stability of solution and numerical simulations of a mathematical model for measles disease, International Journal of Advances in Mathematics, 2019(4), 84-111.[Google Scholor]
- Nigeria-population: Worldometers on world population. (October 2019). https://www.worldometers.info/world- population/nigeria-population/
- Nigeria birth rate from index mundi. (September 2019). Retrieved from https://www.indexmundi.com/ nigeria/birth\_rate.html
- Nigeria Migration Profile. (September 2019). Retrieved from https://www.dailytrust.com.ng/more-foreign-visitors- troop-into-nigeria-data.html.[Google Scholor]
- Nigeria death rate from index mundi. (September 2019) . Retrieved from https://www.indexmundi.com/nigeria /death\_rate.html.
- Trottier, H., & Philippe, P. (2003). Deterministic modeling of infectious diseases: measles cycles and the role of births and vaccination. The Internet Journal of Infectious Diseases, 1(2), https://print.ispub.com/api/0/ispub-article/7099.[Google Scholor]