On Unsteady Flow of a Viscoelastic Fluid Through Rotating Cylinders

1. Introduction

All things are movable and in a fluid state, which is a famous quotation from Thales of Miletos, the first philosopher of Ancient Greece.
The inadequacy of the classical Navier–Stokes theory to describe rheologically complex fluids such as polymer solutions, blood and heavy oils, has led to the development of theories of non-Newtonian fluids. In particular many pastes, slurries, synovial polymer solutions and suspensions exhibit shear thinning behavior. In recent time the study of non-Newtonian fluids has become important. Chemical engineering, food industry, biological analysis, petroleum industry and many other fields use them. The academic workers and engineers are very much interested in the geometry of flows of such types of fluids [1, 2]. In order to describe the non-linear relationship between the stress and the strain rate, numerous models or constitutive equations have been proposed. Models of differential type and rate type have received much attention [3].
In recent years, the fractional Maxwell fluid has obtained a special attention amongst many fluids of rate type, as it includes as special cases the classical Newtonian fluid and the ordinary Maxwell fluid. Fractional calculus has encountered much success in the description of viscoelastic characteristics. The starting point of the fractional derivative model of non-Newtonian model is usually a classical differential equation which is modified by replacing the time derivative of an integer order by the so-called Caputo fractional calculus operator. This generalization allows one to define precisely non-integer order integrals or derivatives [4]. Fractional calculus has been found to be quite flexible in describing viscoelastic behavior [5, 6, 7].
During the past few years, attention has been given to the study on rotating flow of viscoelastic fluids in an annulus. In those studies, the Maxwell model was adopted to describe the viscoelastic fluid. The unidirectional flow of viscoelastic fluid with the fractional Maxwell model was studied by Tan et al. [8, 9] and Hayat et al. [10]. Qi et al. [11, 12] studied the unsteady flow of a viscoelastic fluid with fractional Maxwell model. Recently, Fetecau et al. [13] and Mahmood et al. [14] also studied the flow of fractional Maxwell fluid between coaxial cylinders. There is a vast literature dealing with such fluids, but we shall recall here only a few of the recent papers [15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25,26 ] in cylindrical domains.
The aim of this paper is to establish exact solutions of the velocity field and the shear stress corresponding to the motion of a fractional Maxwell fluid between two infinite circular cylinders. The laplace and finite Hankel transforms are used to solve the problem and the solutions obtained are presented in terms of generalized \(G_{b, c, d}(\cdot, t)\) and \(R_{b, c}(\cdot, t)\) functions. The solutions for ordinary Maxwell and Newtonian fluids are obtained as limiting cases of our general solutions. Furthermore, the solutions for the motion between the cylinders, when one of them is at rest, are also obtained as special cases from our general results. Finally, the influence of the material parameters on the velocity and shear stress of the fluid is analyzed by graphical illustrations.

2. Formulation of the Problem

For the problem under consideration, we choose the cylindrical coordinates \((r, \theta, z)\) and the components of velocity field \(\textbf{w}(r, t)\) are \(w_{r}=0\), \(w_{\theta}=w(r, t)\), \(w_{z}=0\). Since the velocity field \(\textbf{w}\) is independent of \(\theta\) and \(z\), we also assume that the extra-stress tensor \(\textbf{S}\) depends only on \(r\) and \(t\). Furthermore, if the fluid is assumed to be at rest at the moment \(t = 0\), then For an incompressible fluid, the equation of continuity is and in the absence of body forces and pressure gradient, the equation of motion is where \(\rho\) is the density of the fluid, \(D/Dt\) is the material derivative and \(\textbf{T}\) is the stress tensor. According to the above conditions, the constitutive equation and the equation of motion become [11] and respectively Eliminating \(\tau(r,t)\) from Eqs. (4) and (5), we obtain the governing equation of the fluid where \(\nu=\mu/\rho\) is the kinematic viscosity of the fluid.
We consider an incompressible fractional Maxwell fluid at rest in an annular region between two coaxial circular cylinders of radii \(R_1\) and \(R_2(>R_1)\). At time \(t=0^{+}\), both cylinders begin to rotate along their common axis. It is obvious that the motion between the two cylinders is axially symmetric. Owing to the shear, the fluid is gradually moved with the appropriate initial and boundary conditions
where \(\Omega_{1}\) and \(\Omega_{2}\) are constants.

3. Solution of the Problem

In order to solve the problem Eqs. (4) and (6) with initial and boundary conditions (7) and (8), we shall use the Laplace and the Hankel transforms. Laplace transform is used to eliminate the time variable and to eliminate spatial variable, Hankel transform is used. To avoid from lengthy calculations of residues and contours integrals, the discrete inverse Laplace method will be used.

3.1. Calculation of the Velocity Field

Applying the Laplace transform to Eqs. (6) and (8), using (7) and formulae we find that where \(\overline{w}(r,q)=\int_{0}^{\infty}w(r,t)e^{-qt}dt\) is the Laplace transform of \(w(r,t)\) and \(q\) is the transform parameter.
The Hankel transform of \(\overline{w}(r,q)\) is defined as where here \(r_{n}\) are the positive roots of the transcendental equation \(B(R_{1}, r)=0 \) while \(J_{1}(\cdot)\) and \(Y_{1}(\cdot)\) are the first and second kind Bessel functions of 1st order.
Now, applying the Hankel transform to Eq. (9), taking into account the conditions (10) and the identity
we find that In order to obtain the velocity field \(w(r, t)\), we have to apply the inverse transforms (both laplace and Hankel). For this, the above Eq. (14) can be written as Using the formula [27] the inverse Hankel transform of \(\overline{w}_{H}(r_{n},q)\) is given as Finally, using the expansion and the known formulae [28] where the generalized \(G_{b,\, c,\, d}(\cdot, \cdot)\) function is defined by Eqs. (97) and (101) of [28] and applying the discrete inverse Laplace transform to Eq. (17), we obtain the velocity field \(w(r, t)\) under the form

3.2. Calculation of the Shear Stress

Applying the Laplace transform to Eq. (4) and using the condition \((7)_{3}\), we find that where is obtained from Eq. (18) and \begin{align*} \widetilde{B}(rr_{n})=J_{0}(rr_{n})Y_{1}(R_{2}r_{n})-J_{1}(R_{2}r_{n})Y_{0}(rr_{n}). \end{align*} Thus Eq. (24) becomes applying again the discrete inverse Laplace transform as well as using the known relation [28] where the generalized \(R_{b, c}(d,t)\) functions are defined by [28] and the expansion we obtain the shear stress \(\tau(r, t)\) under the form

4. Limiting cases

Case I: Making \(\alpha\rightarrow 1\) into Eqs. (23) and (30), we obtain the velocity field and the shear stress corresponding to an ordinary Maxwell fluid, performing the same motion.
Case II: By now letting \(\lambda\rightarrow 0\) into Eqs. (31) and (32) or \(\alpha\rightarrow 1\) and \(\lambda\rightarrow 0\) into Eqs. (23) and (30), using \(\mathop{\lim}\limits_{\lambda\to 0} \frac{1}{\lambda^{k}}G_{1,\,b,\,k}\left(-\lambda^{-1}, t\right)=\frac{t^{-b-1}}{\Gamma(-b)};\,\,\,b< 0\), we obtain the velocity field and the associated shear stress corresponding to a Newtonian fluid, performing the same motion.

5. Special cases

Making \(a=1\) in Eqs. (23) and (30), the solution for the velocity field and the shear stress are recovered which are identical to [26].
Now making again \(a=0\) in Eqs. (24) and (32), the solutions and the shear stress corresponding to an ordinary Maxwell fluid performing the same motion are recovered [26].
Finally taking \(a=1\) in Eqs. (33) and (34), the solutions for the velocity field and the associated shear stress corresponding to a Newtonian fluid are recovered [26].

6. Conclusions

In this paper, the velocity \(w(r,t)\) and the shear stress \(\tau(r,t)\) corresponding to the flow of an incompressible Maxwell fluid with fractional derivatives, in the annular region between two infinite coaxial circular cylinders, have been determined using the Laplace and finite Hankel transforms. The solutions that have been obtained, written under series form in terms of generalized \(G\) and \(R\)-functions, satisfy all imposed initial and boundary conditions. In the special cases, when \(\alpha\rightarrow1\) or \(\alpha\rightarrow1\) and \(\lambda\rightarrow0\), the corresponding solutions for the ordinary Maxwell and Newtonian fluids are obtained. These solutions satisfy the associated boundary conditions (9), respectively, (10).
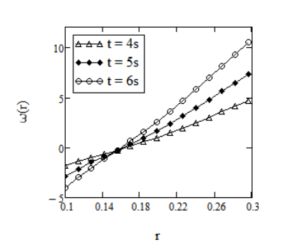
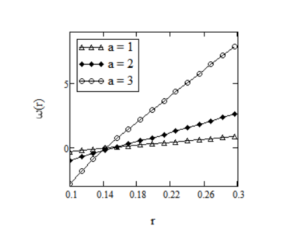
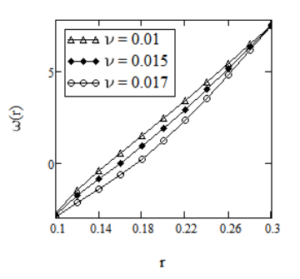
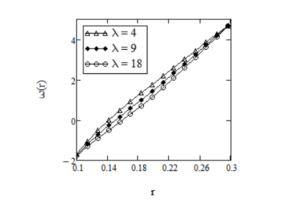
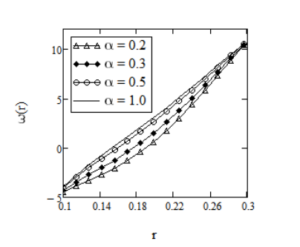
In order to reveal some relevant physical aspects of the obtained results, the diagrams of the velocity field \(w(r,t)\) have been drawn against \(r\) for different values of the time \(t\) and of the material parameters. Figure 1 shows the profile of the fluid motion at different values of time. From these figure one can clearly observe that velocity of the fluid increases with passing time. Effect of power parameter \(a\) on the velocity field is given in Figure 2. It shows that velocity of the fluid is an increasing function of \(a\). In Figures 3 and 4, it is shown that the laxation time \(\nu\) and \(\lambda\) has the same effect on the fluid motion. More exactly, velocity is an increasing function with respect to both \(\nu\) and \(\lambda\). Effect of fractional parameter \(\alpha\) on the fluid motion is represented in Figure 5, it is clearly seen that velocity of the fluid increases as fluid goes to Maxwell fluid.
Finally, for comparison, the diagrams of \(w(r,t)\) corresponding to fractional Maxwell, ordinary Maxwell and Newtonian fluids are together drawn in Figure 6 for the same values of the common material constants and time \(t\). The Newtonian fluid is the swiftest, while the fractional Maxwell fluid is the slowest. One thing is of worth mentioning that units of the material constants are SI units in all figures, and the roots \(r_{n}\) have been approximated by \(n\pi/(R_2-R_1)\).