Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI:10.30538/oms2017.0004
QCD Ghost Dark Energy in Fractal Cosmology
Ines G. Salako, Faiza Gulshan\(^1\)
Département de Physique – Université d’Agriculture, de Kétou BP 13 Kétou, Bénin. (I.G.S)
Department of Mathematics, Lahore Leads University, Lahore-54590, Pakistan. (F.G)
\(^{1}\)Corresponding Author: fazi.gull@yahoo.com
Abstract
Keywords:
1. Introduction
The problem of accelerated expansion is a critical topic in cosmology since its discovery [1]. The main cause of accelerated expansion of the universe is a unknown force so-called dark energy (DE). To explain the nature of DE many cosmologists have proposed many models and theories. Many DE theories for dynamical DE scenario have been proposed to interpret the nature of accelerating universe. A number of DE models have been discussed in this context by many cosmologists. Cosmological constant \(\Lambda\) (\(\Lambda CDM\)) [2] is the simplest candidate for DE (has a constant energy and pressure with constant equation of state). But this model has faced two major problems, cosmic coincidence and fine tuning [2].
In order to describe accelerated expansion phenomenon, two different approaches has been adopted. One is the proposal of various dynamical DE models such as family of chaplygin gas [3], holographic [4, 5], new agegraphic [6], polytropic gas [7], pilgrim [8, 9, 10] \(DE\) models etc. A second approach for understanding this strange component of the universe is modifying the standard theories of gravity, namely, General Relativity (GR) or Teleparallel Theory Equivalent to GR (TEGR). Several modified theories of gravity are \(f(R)\), \(f(T)\) [11, 12, 13, 14, 15, 16], \(f(R,\mathcal{T})\) [17, 18], \(f(G)\) [19, 20, 21, 22, 23] (where \(R\) is the curvature scalar, \(T\) denotes the torsion scalar, \(\mathcal{T}\) is the trace of the energy momentum tensor and \(G\) is the invariant of Gauss-Bonnet defined as \(G=R^2-4R_{\mu\nu}R^{\mu\nu}+ R_{\mu\nu \lambda\sigma}R^{\mu\nu\lambda\sigma}\)). For clear review of DE models and modified theories of gravity, see the reference [24, ].
We arrange the paper as follow: Section 2 describes the basic equations of fractal cosmology. In section 3, we discuss the cosmological parameters (Hubble, Deceleration, EoS) and planes (\(\omega_{D}-\omega'_{D}\), state-finder). In the last section, we conclude our results.
2. Fractal Cosmology
According to Einstein gravity in a fractal space-time, the total action is [25, 26, ]3. QCD Ghost Dark Energy
Recent observations have been proved that Veneziane ghost of chromodynamics QCD is a good model and helps to solve the U(1) problem [27]. Veneziane ghost DE model contribute to the vacuum energy and proportional to \(\Lambda^{3}_{QCD}H\) (smallest \(QCD\) scale), where \(H\) is the Hubble parameter and \(\Lambda_{QCD}\) is the QCD mass scale. GDE is defined as [28, 29, 30, 31, 32] \(\rho_{de}=\alpha H\). This model is discussed for many cosmological parameter theories and observational schemes. Later on, it has been discussed in the form \(H+O(H^{2})\) [33] of Veneziane ghost in QCD has enough vacuum energy by which the early evolution of the universe is explained (with the help of \(H^{2}\)) [34]. This model is called generalized ghost DE model (GGDE). Garcia-Salcedo has proposed a new version of GGDE called QCD ghost DE model which depends on the radius of trapping horizon. For flat universe, it is defined as3.1. Hubble Parameter
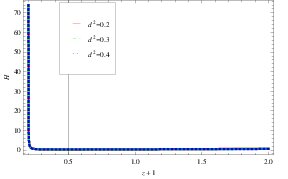
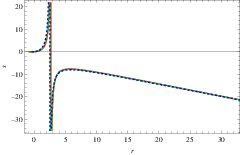
By using Eqs.(7) and (11), we get the Hubble parameter in the formFigure 1. Plots of \(H\) versus \(1+z\) for QCD ghost DE model in fractal Cosmology.
3.2. Deceleration Parameter
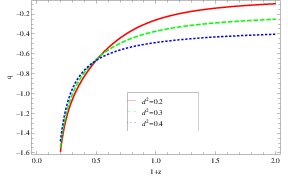
The deceleration parameter is denoted by \(q\). This parameter tells us the transaction phase of the universe, either accelerating (\(-1 \leq q< 0\)) or decelerating (\(q\geq0\)). Its mathematical form isFigure 2. Plots of \(q\) versus \(1+z\) for QCD ghost DE model in fractal cosmology.
3.3. Equation of State Parameter
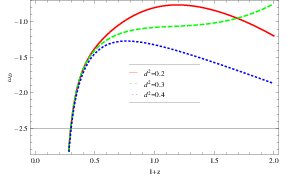
This parameter can be obtained by using Eqs.(9) and (12) as followsFigure 3. Plots of \(\omega_{D}\) versus \(1+z\) for QCD ghost DE model in fractal Cosmology.
3.4. \(\omega_{D}-\omega'_{D}\) plane
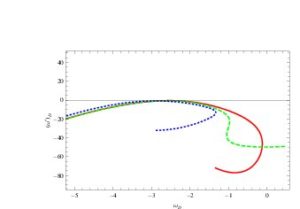
The \(\omega_{D}-\omega'_{D}\) plane characterize thawing as well as the freezing region of universe, i.e., when \(\omega_{D}< 0\) and \({\omega}'_{D}> 0\) then the plane corresponding to thawing region. But if both \(\omega_{D}\) and \({\omega}'_{D}\) are negative, then this plane provides freezing region. Caldwell and Linder [35] discover this method. By taking derivative of Eq.(15), we obtainFigure 4. Plots of \(\omega_{D}-\omega’_{D}\) for QCD ghost DE model in fractal cosmology.
3.5. \(r-s\) plane
With the help of this plane, we can identify different DE models. Trajectories of different DE models have different ranges in this plane. For example, \(\{r,s\}=\{1,0\}\) corresponds to \(\Lambda CDM\) model, \(\{r,s\}=\{1,1\}\) shows \(CDM\) limit, \(\{s>0,r< 1\}\) shows phantom and quintessence while \(\{s< 0,r >1\}\) denotes chaplygin gas region. Mathematical form of state-finder parameters are given by [36]Figure 5. Plots of \(r-s\) for QCD ghost DE model in fractal Cosmology.
4. Concluding Remarks
We have investigated the physical significance of QCD ghost DE model in fractal universe by developing various cosmological parameters as well as cosmological planes. These parameters as well as planes shamefully explain the current cosmic acceleration.Competing Interests
The author(s) do not have any competing interests in the manuscript.References
- Riess, A. G. et. al. (1998). Observational evidence from supernovae for an accelerating universe and a cosmological constant. The Astronomical Journal, 116(3), 1009-1038.[Google Scholor]
- Weinberg, S. (1989). The cosmological constant problem. Reviews of modern physics, 61(1), 1-23. [Google Scholor]
- Kamenshchik, A., Moschella, U., & Pasquier, V. (2001). An alternative to quintessence. Physics Letters B, 511(2), 265-268. [Google Scholor]
- Hsu, S. D. (2004). Entropy bounds and dark energy. Physics Letters B, 594(1), 13-16. [Google Scholor]
- Li, M. (2004). A model of holographic dark energy. Physics Letters B, 603(1), 1-5. [Google Scholor]
- Wei, H., & Cai, R. G. (2008). A new model of agegraphic dark energy. Physics Letters B, 660(3), 113-117. [Google Scholor]
- Karami, K., Ghaffari, S., & Fehri, J. (2009). Interacting polytropic gas model of phantom dark energy in non-flat universe. The European Physical Journal C-Particles and Fields, 64(1), 85-88. [Google Scholor]
- Wei, H. (2012). Pilgrim dark energy. Classical and Quantum Gravity, 29(17), 175008. [Google Scholor]
- Sharif, M., & Jawad, A. (2013). Pilgrim dark energy with apparent and event horizons in non-flat universe. The European Physical Journal C, 73(10), 2600, 1-10. [Google Scholor]
- Shamaila, S., Zafar, N., Riaz, S., Sharif, R., Nazir, J., & Naseem, S. (2016). Gold nanoparticles: an efficient antimicrobial agent against enteric bacterial human pathogen. Nanomaterials, 6(4), 71, 2-10. [Google Scholor]
- Amorós, J., de Haro, J., & Odintsov, S. D. (2013). Bouncing loop quantum cosmology from \(F(T)\) gravity. Physical Review D, 87(10), 104037. [Google Scholor]
- Linder, E. V. (2010). Einstein’s Other Gravity and the Acceleration of the Universe. Physical Review D, 81(12), 127301. [Google Scholor]
- Jamil, M., Momeni, D., & Myrzakulov, R. (2013). Wormholes in a viable \(F(T)\) gravity. The European Physical Journal C, 73(1), 2267. [Google Scholor]
- Myrzakulov, R. (2012). Cosmology of \(F(T)\) Gravity and k-Essence. Entropy, 14(9), 1627-1651. [Google Scholor]
- Salako, I. G., Rodrigues, M. E., Kpadonou, A. V., Houndjo, M. J. S., & Tossa, J. (2013). \(\Lambda\)CDM model in \(f(T)\) gravity: reconstruction, thermodynamics and stability. J. Cosmol. Astropart. Phys, 11(060), 1307-0730. [Google Scholor]
- Rodrigues, M. E., Salako, I. G., Houndjo, M. J. S., & Tossa, J. (2014). Locally rotationally symmetric Bianchi type-I cosmological model in \(F(T)\) gravity: from early to dark energy dominated universe. International Journal of Modern Physics D, 23(01), 1450004. [Google Scholor]
- Baffou, E. H., Kpadonou, A. V., Rodrigues, M. E., Houndjo, M. J. S., & Tossa, J. (2015). Cosmological viable \(f(R,T)\) dark energy model: dynamics and stability. Astrophysics and Space Science, 356(1), 173-180. [Google Scholor]
- Houndjo, M. J. S. (2012). Reconstruction of \(f(R,T)\) gravity describing matter dominated and accelerated phases. International Journal of Modern Physics D, 21(01), 1250003. [Google Scholor]
- Nojiri, S. I., & Odintsov, S. D. (2005). Modified Gauss–Bonnet theory as gravitational alternative for dark energy. Physics Letters B, 631(1),1-6. [Google Scholor]
- Bamba, K., Odintsov, S. D., Sebastiani, L., & Zerbini, S. (2010). Finite-time future singularities in modified Gauss–Bonnet and $F(R,G)$ gravity and singularity avoidance. The European Physical Journal C, 67(1-2), 295-310. [Google Scholor]
- Bamba, K., Geng, C. Q., Nojiri, S. I., & Odintsov, S. D. (2010). Equivalence of the modified gravity equation to the Clausius relation. EPL (Europhysics Letters), 89(5), 50003. [Google Scholor]
- Rodrigues, M. E., Houndjo, M. J. S., Momeni, D., & Myrzakulov, R. (2013). A type of Levi–Civita solution in modified Gauss–Bonnet gravity. Canadian Journal of Physics, 92(2), 173-176. [Google Scholor]
- Houndjo, M. J. S., Rodrigues, M. E., Momeni, D., & Myrzakulov, R. (2014). Exploring cylindrical solutions in modified \(f(G)\) gravity. Canadian Journal of Physics, 92(12), 1528-1540. [Google Scholor]
- Bamba, K., Capozziello, S., Nojiri, S. I., & Odintsov, S. D. (2012). Dark energy cosmology: the equivalent description via different theoretical models and cosmography tests. Astrophysics and Space Science, 342(1), 155-228.[Google Scholor]
- Calcagni, G. (2010). Fractal universe and quantum gravity. Physical review letters, 104(25), 251301. [Google Scholor]
- Calcagni, G. (2010). Quantum field theory, gravity and cosmology in a fractal universe. Journal of High Energy Physics, 2010(3),120. [Google Scholor]
- Elizalde, E., Nojiri, S. I., Odintsov, S. D., & Wang, P. (2005). Dark energy: vacuum fluctuations, the effective phantom phase, and holography. Physical Review D, 71(10), 103504. [Google Scholor]
- Yang, W. Q., Wu, Y. B., Song, L. M., Su, Y. Y., Li, J., Zhang, D. D., & Wang, X. G. (2011). Reconstruction of new holographic scalar field models of dark energy in brans–dicke universe. Modern Physics Letters A, 26(03), 191-204. [Google Scholor]
- Granda, L. N., & Oliveros, A. (2008). Infrared cut-off proposal for the holographic density. Physics Letters B, 669(5), 275-277. [Google Scholor]
- Sheykhi, A. (2009). Interacting holographic dark energy in Brans–Dicke theory. Physics Letters B, 681(3), 205-209. [Google Scholor]
- Jamil, M., & Sheykhi, A. (2011). Interacting entropy-corrected agegraphic-tachyon dark energy. International Journal of Theoretical Physics, 50(3), 625-636. [Google Scholor]
- Jamil, M., Momeni, D., & Myrzakulov, R. (2012). Stability of a non-minimally conformally coupled scalar field in \(F (T)\) cosmology. The European Physical Journal C, 72(7), 2075. [Google Scholor]
- Zhitnitsky, A. R. (2012). Contact term, its holographic description in QCD and dark energy. Physical Review D, 86(4), 045026. [Google Scholor]
- Cai, R. G., Tuo, Z. L., Wu, Y. B., & Zhao, Y. Y. (2012). More on QCD ghost dark energy. Physical Review D, 86(2), 023511. [Google Scholor]
- Caldwell, R. R., & Linder, E. V. (2005). Limits of quintessence. Physical review letters, 95(14), 141301. [Google Scholor]
- Sahni, V., Saini, T. D., Starobinsky, A. A., & Alam, U. (2003). Statefinder—a new geometrical diagnostic of dark energy. JETP Letters, 77(5), 201-206. [Google Scholor]