Ontology Similarity Computing Based on Stochastic Primal Dual Coordinate Technique

1. Introduction

Ontologies play an increasingly important role in the fields of software engineering, artificial intelligence, information retrieval, and Web services. According to the degree of domain dependence, the ontology can be divided into Top Ontology, Domain Ontology, Task Ontology and Application Ontology. As a kind of description framework and standard specification of knowledge, it is the representation of related concepts and the relationship between concepts. It selects general terms and concepts in the fields described, and uses ontology language to define and describe. Standard universal unambiguous domain ontology. Domain ontology is a tool for knowledge exchange and sharing between designers and systems. It facilitates the processing of structured knowledge and supports semantic operations. It has been widely used in knowledge management and data mining. The introduction of ontology concept promotes the integration of traditional information retrieval mechanism and semantic content, which can effectively improve the search efficiency and search accuracy of knowledge. Several algorithms and related results on ontology can refer to Wang et al. [1], Cheng et al. [2], Peng et al. [3], Zhang et al. [4], Zhang et al. [5], Zhang et al. [6], Xue and Pan [7], Zhong et al. [8], Jiang et al. [9], and Liang [10].

With the advent of the era of big data, the ontology needs to deal with not only text concepts, but also images, audio and video. Therefore, machine learning algorithms have been widely used in ontology similarity calculations in recent years. A classic method is to learn the ontology function through ontology sample set, this ontology function maps the whole ontology graph to a one-dimensional real number, and each ontology vertex corresponds to a real number. The similarity of the concepts is judged by comparing the distances between the real numbers. Since the information of each ontology vertex is expressed as a \(p\)-dimensional vector, the ontology function can be regarded as a map \(f: \Bbb R^{p}\to \Bbb R\). In this paper, we present an ontology learning algorithm for ontology similarity measuring and ontology mapping by means of stochastic primal dual coordinate trick.

2. Setting

First, we use a \(p\)-dimensional vector to express all the information of a vertex \(v\) (corresponding to a concept). For convenience, we use \(v\) to denote vertex, vector and concept as well. Assume that \(\{v_{i}\}_{i=1}^{n}\) is the ontology sample set, \(n\) is the capacity of ontology sample, \(\{l_{i}\}_{i=1}^{n}\) are the ontology loss function, \(\beta\) is the ontology sparse vector, and \(g\) is the punish function. In this way, to learn an optimal ontology function can be transform to learn an ontology sparse vector \(\beta\), and generally the optimization model can be formulated as

where \(\lambda\) is a positive balance parameter. For example, in the setting of mixture norm punishment, the punish function can be expressed as \(g(\beta)=\|\beta\|_{1}+\|\beta\|_{2}^{2}\).

Let \({\bf V}\in\Bbb R^{n\times p}\) be the ontology information matrix which is denoted as \({\bf V}=[v_{1},\cdots,v_{n}]^{T}\), and its \(j\)-th column is denoted as \({\bf V}_{:j}\). Let \(\{l_{i}^{*}\}_{i=1}^{n}\) be the convex conjugate function of \(\{l_{i}\}_{i=1}^{n}\), and \(g^{*}\) be the convex conjugate function of \(g\). Then, the dual problem of ontology problem (1) can be written as

Assume that ontology loss functions \(l_{i}\) are \(\frac{1}{\gamma}\)-smooth. Using the standard stochastic primal-dual coordinate method for regularized empirical risk minimization, we can get the following implementation process (see Zhang and Xiao [11] for more details). First, input mini-batch size \(a\), \(\beta^{0}\), \(\alpha^{0}\) as initial solutions, \(\overline{\beta}^{0}\gets\beta^{0}\), \(\overline{\alpha}^{0}\gets\alpha^{0}\). Then, for \(t=1,2,\cdots\) to converged do: Generate random index from sampling probability \(p\)(in Zhang and Xiao [11], \(p_{i}=\frac{1}{2n}+\frac{\|v_{i}\|_{2}}{2\sum_{k\in\{1,\cdots,n\}}\|v_{k}\|_{2}}\)) \(a\) times with replacement (denote \(K\) as the set of random indices); set \(\sigma_{i}\) and \(\tau\) as parameters depend on \(p\), and \(\theta=\max\{1-2\tau\lambda,1-(\max_{i\in\{1,\cdots,n\}}\frac{1}{ap_{i}}+\frac{n}{2a\sigma_{i}\gamma})^{-1}\}\). Then update the dual and the primal coordinates \(\alpha_{i}^{t+1}={\rm argmax}_{{\bf w}\in\Bbb R}\{-{\bf w}< v_{i},\overline{\beta}^{t}>-l_{i}^{*}(-{\bf w})-\frac{np_{i}}{2\sigma_{i}}({\bf w}-\alpha_{i}^{t})^{2}\}\) if \(i\in K\) (otherwise, \(\alpha_{i}^{t+1}=\alpha_{i}^{t}\)), \(\overline{\alpha}_{i}^{t+1}=\alpha_{i}^{t}+\frac{(\alpha_{i}^{t+1}-\alpha_{i}^{t})}{ap_{i}n}\) for \(i\in\{1,\cdots,n\}\), \(\beta^{t+1}={\rm argmin}_{\beta\in\Bbb R^{p}}\{\lambda g(\beta)-\frac{1}{n}\beta^{T}{\bf V}^{T}\overline{\alpha}^{t+1}+\frac{\|\beta-\beta^{t}\|_{2}^{2}}{2\tau}\}\), and \(\overline{\beta}^{t+1}=\beta^{t+1}+\theta(\beta^{t+1}-\beta^{t})\).

3. Ontology learning algorithm using stochastic primal dual coordinate trick

Now, in this section, we introduce the trick of ontology optimization algorithm in terms of stochastic primal dual coordinate techniques. Set dual optimality violation \(\kappa_{i}^{t}\) for \(i\in\{1,\cdots,n\}\) and each iteration \(t\) as \noindent Hence, the sampling probability is set as (if \(\kappa_{i}\ne0\))

and \(p_{i}=0\) otherwise. Then, the above stochastic primal dual coordinate based ontology implementation can be modified as follows. Input mini-batch size \(a\), \(\beta^{0}\), and \(\alpha^{0}\); for \(t=1,2,\cdots\) to converged do: \(\alpha_{i}^{t}\gets\) update(\(\alpha_{i}^{t-1}\)) (for \(i\in\{1,\cdots,n\}\)), \(\beta^{t}\gets\) update(\(\beta^{t-1}\)), determine \(\kappa^{t}\) and \(p\) using (4), \((\widehat{\beta}^{0},\widehat{\alpha}^{0})\gets (\beta^{t},\alpha^{t})\), after the inner loop do \((\beta^{t},\alpha^{t})\gets(\widehat{\beta}^{u},\widehat{\alpha}^{u})\) if \(P_{\lambda}(\widehat{\beta}^{u})-D_{\lambda}(\widehat{\alpha}^{u})< P_{\lambda}(\beta^{t})-D_{\lambda}(\alpha^{t})\); for inner loop \(u=1,\cdots,\lceil\frac{n}{a}\rceil\), randomly pick up a subset indices \(K\), \(\widehat{\alpha}_{i}^{u}\gets\) update(\(\widehat{\alpha}_{i}^{u-1}\)) if \(i\in K\), and \(\widehat{\beta}^{u}\gets\) update(\(\widehat{\beta}^{u-1}\)).

By setting \(\psi_{j}^{t}=|\beta_{j}^{t}-\nabla g_{j}^{*}(\frac{{\bf V}_{:j}^{T}\alpha^{t}}{n\lambda})|\), the the above stochastic primal dual coordinate based ontology implementation can be further modified as follows. Input mini-batch size \(a\), \(\beta^{0}\), and \(\alpha^{0}\); for \(t=1,2,\cdots\) to converged do: \(\alpha_{i}^{t}\gets\) update(\(\alpha_{i}^{t-1}\)) (for \(i\in\{1,\cdots,n\}\)), \(\beta^{t}\gets\) update(\(\beta^{t-1}\)), determine \(\kappa^{t}\), \(\psi_{j}^{t}\) and \(p\) using (4), \((\widehat{\beta}^{0},\widehat{\alpha}^{0})\gets (\beta^{t},\alpha^{t})\), after the inner loop do \((\beta^{t},\alpha^{t})\gets(\widehat{\beta}^{u},\widehat{\alpha}^{u})\) if \(P_{\lambda}(\widehat{\beta}^{u})-D_{\lambda}(\widehat{\alpha}^{u})< P_{\lambda}(\beta^{t})-D_{\lambda}(\alpha^{t})\); for inner loop \(u=1,\cdots,\lceil\frac{n}{a}\rceil\), randomly pick up a subset indices \(K\), \(\widehat{\alpha}_{i}^{u}\gets\) update(\(\widehat{\alpha}_{i}^{u-1}\)) if \(i\in K\), and \(\widehat{\beta}_{j}^{u}\gets\) update(\(\widehat{\beta}_{j}^{u-1}\)) for \(j\in\{m\in\{1,\cdots,p\},\psi_{m}^{t}\ne0\}\).

At last, one remark is that if we randomly pick up a subset \(M_{h}\) follows the probability vector \(q\), then the iterative process presented in last section can be re-written as follows. First, input dual mini-batch size \(a\), primal mini-batch size \(b\), \(\beta^{0}\), \(\alpha^{0}\) as initial solutions, \(\overline{\beta}^{0}\gets\beta^{0}\), \(\overline{\alpha}^{0}\gets\alpha^{0}\). Partition the indices of primal variables into \(p\) mod b mini-batches whose the number of elements are \(b+1\) and (\(\lfloor\frac{p}{b}\rfloor-p\) mod \(b\)) mini-batches whose the number of elements are \(b\). For \(t=1,2,\cdots\) to converged do: Generate random index from sampling probability \(p\) \(a\) times with replacement (denote \(K\) as the set of random indices); randomly pick up a subset \(M_{h}\) follows the probability vector \(q\); update the dual and the primal coordinates \(\alpha_{i}^{t+1}={\rm argmax}_{{\bf w}\in\Bbb R}\{-{\bf w}< v_{i},\overline{\beta}^{t}>-l_{i}^{*}(-{\bf w})-\frac{np_{i}}{2\sigma_{i}}({\bf w}-\alpha_{i}^{t})^{2}\}\) if \(i\in K\) (otherwise, \(\alpha_{i}^{t+1}=\alpha_{i}^{t}\)), \(\overline{\alpha}_{i}^{t+1}=\alpha_{i}^{t}+\frac{(\alpha_{i}^{t+1}-\alpha_{i}^{t})}{ap_{i}n}\) for \(i\in\{1,\cdots,n\}\), \(\beta_{j}^{t+1}={\rm argmin}_{x\in\Bbb R}\{\lambda g(x)-\frac{x}{n}< {\bf V}_{:j},\overline{\alpha}^{t+1}>+\frac{q M_{h} p}{2\tau|M_{h}|}(x-\beta_{j}^{t})^{2}\}\) if \(j\in M_{h}\) (otherwise, \(\beta_{j}^{t+1}=\beta_{j}^{t}\)), and \(\overline{\beta}^{t+1}=\beta^{t+1}+\theta(\beta^{t+1}-\beta^{t})\).

4. Experiments

Four simulation experiments relating the ontology similarity measure and ontology mapping are designed below. In order to adjacent to the setting of ontology algorithm, a \(p\)-dimensional vector is applied to express the information of each vertex. The information includes the name, instance, attribute and structure of a vertex. Here the instance of vertex is used to express the set of the reachable vertex in the directed ontology graph. The effectiveness of main ontology algorithm is verified in the following two experiments.

4.1. Ontology similarity measure experiment on plant data

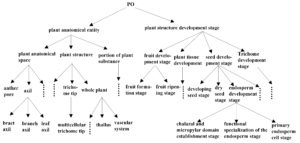
In the first experiment, ''PO'' ontology built in http: //www.plantontology.org. was adopted to test the efficiency of the proposed new algorithm for ontology similarity measuring. The basic structure of ''PO'' is shown in Figure 1. \(P@N\) standard was also used for this experiment. Furthermore, ontology methods discussed in [12], [13] and [14] for the ''PO'' ontology were considered as well. The accuracies of these three algorithms were calculated to compare with that obtained through the algorithm proposed in the paper. Table 1 presents part of the data.

We first give the closest \(N\) concepts for every vertex on the ontology graph by experts in plant field, and then we obtain the first \(N\) concepts for every vertex on ontology graph by the our algorithm, and compute the precision ratio.

Table 1. The experiment results of ontology similarity measure.

\quad	\(P\)@3 average	\(P\)@5 average	\(P\)@10 average
\quad	precision ratio	precision ratio	precision ratio
Algorithm in our paper	0.4892	0.5739	0.7103
Algorithm in [12]	0.4549	0.5117	0.5859
Algorithm in [13]	0.4282	0.4849	0.5632
Algorithm in [14]	0.4831	0.5635	0.6871

When \(N\)= 3, 5, or 10, the precision ratio obtained by the proposed algorithm is higher than those determined by the algorithms in [12], [13] and [14]. In particular, the precision ratios of those algorithms increase significantly as \(N\) increases. It can be concluded that the algorithm described in our paper is superior to those proposed in [12], [13] and [14].

4.2. Ontology mapping experiment on humanoid robotics data

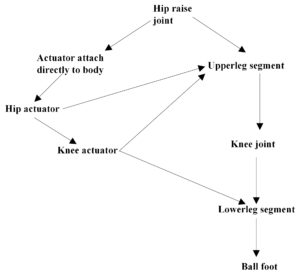
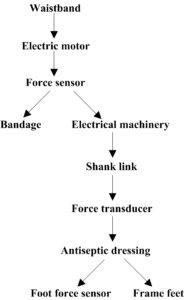
Humanoid robotics ontologies \(O_{2}\) and \(O_{3}\) which were applied for our second experiment. Figure 2 and Figure 3 exhibit the structures of \(O_{2}\) and \(O_{3}\), respectively. This experiment is to determine ontology mapping between \(O_{2}\) and \(O_{3}\) by our algorithm. Likewise, the authors applied \(P@N\) criterion to measure the equality of the experiment. The ontology algorithms used in [15], [13] and [14] to humanoid robotics ontologies were employed. Then the precision ratios of these three methods were compared with that of the proposed algorithm. The experimental results are demonstrated in Table 2.

Table 2. The experiment results of ontology mapping.

\quad	\(P\)@1 average	\(P\)@3 average	\(P\)@5 average
\quad	precision ratio	precision ratio	precision ratio
Algorithm in our paper	0.2778	0.5000	0.5667
Algorithm in [15]	0.2778	0.4815	0.5444
Algorithm in [13]	0.2222	0.4074	0.4889
Algorithm in [14]	0.2778	0.4630	0.5333

The experimental results in Table 2 reveal that our algorithm performs more efficiently than those described in [15], [13] and [14], particularly when \(N\) is large enough.

Conflict of Interests

The authors hereby declare that there is no conflict of interests regarding the publication of this paper.