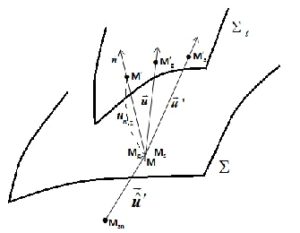
Let \(M\) a point of \(\Sigma\). We denote by \(M_{g}\), \(M_{s}\) the particles of the gas and of the elastic body that are in \(M\) at the instant \(t=0\). These particles come in \(M'_{g}\), \(M'_{s}\) on \(\Sigma_{t}\) at the instant \(t\):
\[
\overrightarrow{MM'_{g}}=\vec{u}\qquad ;\qquad \overrightarrow{MM'_{s}}=\vec{u}'
\]
In linear theory, we admit that the unit vectors normal to
\( \Sigma_{t}\) in \( M'_{g}\) and \( M'_{s}\) are equipollent to the unit vector \(\vec{n}\) normal in
\(M\) to \(\Sigma\) and that the pressure of the gas \(P\) in \(M'_{g}\) is equal to the pressure of the gas in \(M'\), intersection of \(\Sigma_{t}\) with the normal in \(M\) to \(\Sigma\).
The dynamic conditions on \(\Sigma_{t}\) are
\begin{equation*}
\sigma'_{ij}(\vec{\hat{u}}'+\vec{u}')n_{j}=-{P}(M',t)n_{i} \;.
\end{equation*}
Or, using the second condition (2):
\begin{equation*}
\sigma'_{ij}(\vec{u}')n_{j}=-[{P}(M',t)-p_{0}(M) ]\cdot n_{i}\qquad \text{on} \;\; \Sigma \;.
\end{equation*}
We have
\[
{P}(M',t)={P}(M + u_{n|\Sigma} \vec{n},t)=\mathcal{P}(M,t)+\overrightarrow{\text{grad}}{P}(M)\cdot u_{n|\Sigma} \vec{n}+\cdots
\]
Since \(u_{n|\Sigma}\) is of the first order, we can, in linear theory, replace \(\overrightarrow{\text{grad}}{P}(M,t)\) by
\[
\overrightarrow{\text{grad}}p_{0}=- \rho_{0}\,g\vec{x}_{3}\;,
\]
so that
\[
{P}(M',t)={P}(M,t)-\rho_{0} g \, u_{n|\Sigma}\; n_{3|\Sigma}+\cdots
\]
and finally
\begin{equation}
\label{eq16}
\sigma'_{ij}(\vec{u}')n_{j}=[-p(M,t)+\rho_{0|_\Sigma} g n_{3|\Sigma}\;u_{n|\Sigma}]n_{i}\qquad \text{on} \;\; \Sigma \;.
\end{equation}
(16)
Let us call \(\overrightarrow{T}_t \left( \vec{u}' \right)_{|\Sigma}\) the tangential stress and \({T}_n \left( \vec{u}' \right)_{|\Sigma}\) the normal stress; we have
\begin{equation}
\label{eq17}
\overrightarrow{T}_t \left( \vec{u}' \right)_{|\Sigma}=0\quad;\quad {T}_n \left( \vec{u}' \right)_{|\Sigma}=
-p_{|\Sigma}+\rho_{0|_\Sigma} g n_{3|\Sigma}\;u_{n|\Sigma}\;.
\end{equation}
(17)
4. The auxiliary problem
Case 1. We introduce the following auxiliary problem:
\begin{equation}
\label{eq18}
-\frac{\partial \sigma'_{ij}(\vec{u}')}{\partial x_{j}}=0
\quad \text{in} \quad \Omega'
\quad;\quad \vec{u}'_{|_{S}}=0
\quad;\quad u'_{n|\Sigma}=u_{n|\Sigma}
\quad;\quad \overrightarrow{T}_t \left( \vec{u}' \right)_{|\Sigma}=0\;,
\end{equation}
(18)
where \(u_{n|\Sigma}\) is considered as a datum.
It is the problem of the motion of an elastic body when the motion of the gas is known and we seek the solution of this auxiliary problem in the space.
\[
\widehat{\Xi}^1(\Omega')\overset{\text{def}}{=}\left\{
\vec{u}' \in {\Xi}^{1}(\Omega')\overset{\text{def}}{=}\left[ H^1(\Omega')\right]^3;\;\; \vec{u}'_{|S}=0
\right\} \;.
\]
Then \(u'_{n|\Sigma} \in H^{1/2}(\Sigma)\) and consequently, we suppose that \(u_{n|\Sigma} \in H^{1/2}(\Sigma)\).
Case 2. Let \(\overrightarrow{\Phi}\) an element of \(\widehat{\Xi}^1(\Omega')\) such that
\(\Phi_{n|\Sigma} =u_{n|\Sigma}\in H^{1/2}(\Sigma) \).
In the following, we will see the construction of such \(\overrightarrow{\Phi}\). We denote by \(V_0\) the subspace of \(\hat{\Xi}^1(\Omega')\) defined by
\[
V_0=
\left\{
\vec{v}_0 \in \widehat{\Xi}^1(\Omega')\quad; \quad
v_{0n|\Sigma}=0
\right\}
\]
and we seek the solution \(\vec{u}'\) of the auxiliary problem in the form
\[
\vec{u}'=\overrightarrow{\Phi}+\vec{v}_0\;.
\]
The auxiliary problem (18) becomes a problem for \(\vec{u}_0 \in V_0\):
\begin{equation}
\label{eq19}
-\frac{\partial \sigma'_{ij}(\vec{u}_0)}{\partial x_{j}}=\frac{\partial \sigma'_{ij}(\overrightarrow{\Phi})}{\partial x_{j}}
\quad \text{in} \quad \Omega'
\quad;\quad {u}_{0n|\Sigma}=0
\quad;\quad
\overrightarrow{T}_t \left( \vec{u}'_0 \right)_{|\Sigma}=
- \overrightarrow{T}_t ( \overrightarrow{\Phi})_{|\Sigma}\;.
\end{equation}
(19)
Let us seek a variational formulation of this problem.
We have, for each \(\vec{v}_0\in V_0\):
\[
- \int_{\Omega'}
\frac{\partial \sigma'_{ij}(\vec{u}_0)}{\partial x_{j}} \cdot \bar{v}_{0i}
\, \mathrm d\Omega'
=
\int_{\Omega'}
\frac{\partial \sigma'_{ij}(\overrightarrow{\Phi})}{\partial x_{j}}
\cdot \bar{v}_{0i}
\, \mathrm d\Omega'
\]
or
\[
\begin{aligned}
&
- \int_{\Omega'}
\left[
\frac{\partial}{\partial x_{j}}[ \sigma'_{ij}(\vec{u}_0) \bar{v}_{0i} ]
- \sigma'_{ij}(\vec{u}_0)\epsilon'_{ij}(\bar{\vec{v}}_0)
\right]
\, \mathrm d\Omega'
\\
&\qquad
=
\int_{\Omega'}
\left[
\frac{\partial}{\partial x_{j}}[ \sigma'_{ij}(\overrightarrow{\Phi}) \bar{v}_{0i} ]
- \sigma'_{ij}(\overrightarrow{\Phi})\epsilon'_{ij}(\bar{\vec{v}}_0)
\right]
\, \mathrm d\Omega'
\;,
\end{aligned}
\]
or, using the Green's formula and denoting by \(\vec{n}_\text{e}\), the external normal unit vector to \(\partial \Omega'\):
\[
\begin{aligned}
&
-\int_{S}
\sigma'_{ij}(\vec{u}_0) {n}_\text{ej} \bar{v}_{0i} \, \mathrm dS
-\int_{\Sigma}
\sigma'_{ij}(\vec{u}_0) {n}_\text{ej} \bar{v}_{0i} \, \mathrm d\Sigma
+ \int_{\Omega'}
\sigma'_{ij}(\vec{u}_0)\epsilon'_{ij}(\bar{\vec{v}}_0)
\, \mathrm d\Omega'
\\
&\qquad
=
\int_{S}
\sigma'_{ij}(\overrightarrow{\Phi}) {n}_\text{ej} \bar{v}_{0i} \, \mathrm dS
+
\int_{\Sigma}
\sigma'_{ij}(\overrightarrow{\Phi}) {n}_\text{ej} \bar{v}_{0i} \, \mathrm d\Sigma
-
\int_{\Omega'}
\sigma'_{ij}(\overrightarrow{\Phi})\epsilon'_{ij}(\bar{\vec{v}}_0)
\, \mathrm d\Omega'
\;.
\end{aligned}
\]
The integrals on \(S\) disappear since \(\vec{v}_{0|S}=0\)
and the integrals on \(\Sigma\) disappear by virtue of (19).
The variational formulation of the problem
for \(\vec{u}_0\) is to find \(\vec{u}_0 \in V_0\) such that
\begin{equation}
\label{eq20}
\int_{\Omega'}
\sigma'_{ij}(\vec{u}_0)\epsilon'_{ij}(\bar{\vec{v}}_0)
\, \mathrm d\Omega'
= -
\int_{\Omega'}
\sigma'_{ij}(\overrightarrow{\Phi})\epsilon'_{ij}(\bar{\vec{v}}_0)
\, \mathrm d\Omega' \quad \forall \vec{v}_0 \in V_0
\;.
\end{equation}
(20)
Conversely, let \(\vec{u}_0\) a function of \(t\) with values in \(V_0\) and verifying (20).
We have
\[
\int_{\Omega'}
\frac{\partial \sigma'_{ij}(\vec{u}_0)}{\partial x_{j}} \cdot \bar{v}_{0i}
\, \mathrm d\Omega'
=
\int_{\Omega'}
\left[
\frac{\partial}{\partial x_{j}}[ \sigma'_{ij}(\vec{u}_0) \bar{v}_{0i} ]
- \sigma'_{ij}(\vec{u}_0)\epsilon'_{ij}(\bar{\vec{v}}_0)
\right]
\, \mathrm d\Omega'
\]
and an anlogous equation by replacing \(\vec{u_0}\) by \(\overrightarrow{\Phi}\).
Using (20), we obtain
\[
- \int_{\Omega'}
\frac{\partial \sigma'_{ij}(\vec{u}_0)}{\partial x_{j}} \cdot \bar{v}_{0i}
\, \mathrm d\Omega'
+
\int_{\Sigma}
\sigma'_{ij}(\vec{u}_0) {n}_\text{ej} \bar{v}_{0i} \, \mathrm d\Sigma
=
\int_{\Omega'}
\frac{\partial \sigma'_{ij}(\overrightarrow{\Phi})}{\partial x_{j}} \cdot \bar{v}_{0i}
\, \mathrm d\Omega'
-
\int_{\Sigma}
\sigma'_{ij}(\overrightarrow{\Phi}) {n}_\text{ej} \bar{v}_{0i} \, \mathrm d\Sigma \;.
\]
Taking \(\vec{v}\in \left[ \mathscr{D} (\Omega')\right]^3 \subset V_0\), we have
\[
- \frac{\partial \sigma'_{ij}(\vec{u}_0)}{\partial x_{j}}
=
\frac{\partial \sigma'_{ij}(\overrightarrow{\Phi})}{\partial x_{j}} \quad \text{in}\quad \mathscr{D}
(\Omega') \;.
\]
Taking into account of \(v_{0n|\Sigma}=0\), we have
\[
\int_{\Sigma}
\overrightarrow{T}_{t}(\vec{u}_0)\cdot \vec{v}_{0t|\Sigma}
\, \mathrm d\Sigma
=
- \int_{\Sigma}
\overrightarrow{T}_{t}(\overrightarrow{\Phi})\cdot \vec{v}_{0t|\Sigma}
\, \mathrm d\Sigma \;,
\]
and, since \(\vec{v}_{0t|\Sigma}\) is arbitrary
\[
\overrightarrow{T}_{t}(\vec{u}_{0})_{|\Sigma}
=
- \overrightarrow{T}_{t}(\overrightarrow{\Phi})_{|\Sigma}
\]
and we find the auxiliary problem.
Let us return to its variational formulation (20).
The left-hand side can be considered as a scalar product in \(V_0\):
\[
\int_{\Omega'}
\sigma'_{ij}(\vec{u}_0)\epsilon'_{ij}(\bar{\vec{v}}_0)
\, \mathrm d\Omega'
=\left(\vec{u}_0, \vec{v}_0 \right)_ {V_0}
\;,
\]
The associated norm \(\left\| \vec{u}_{0} \right\|_{V_0}\) being classically equivalent in \(V_0\) to the norm \(\left\| \vec{u}_{0} \right\|_{1}\) of
\( {\Xi}^1(\Omega')\).
Since \( \vec{u}_0 \in V_0 \subset \widehat{\Xi}^1(\Omega')\), we have
\[
\left(\vec{u}_0, \vec{v}_0 \right)_ {V_0}
=
\int_{\Omega'}
\sigma'_{ij}(\vec{u}_0)\epsilon'_{ij}(\bar{\vec{v}}_0)
\, \mathrm d\Omega'
=
\left(\vec{u}_0, \vec{v}_0 \right)_ {\widehat{\Xi}^1(\Omega')}
\;.
\]
Setting \(\vec{v}_0=\vec{u}_0\), we have
\[
\left\| \vec{u}_0\right\|_{V_0}
=
\left\| \vec{u}_0\right\|_{\widehat{\Xi}^1(\Omega')}
\quad
\forall \vec{u}_0 \in V_0
\;.
\]
The variational Equation (20) can be written as
\begin{equation}
\label{eq21}
\left(\vec{u}_0, \vec{v}_0 \right)_ {V_0}
=
- \left(\overrightarrow{\Phi}, \vec{v}_0 \right)_ {\widehat{\Xi}^1(\Omega')}
\quad \forall \vec{v}_0 \in V_0
\;.
\end{equation}
(21)
But, we have
\[
\left|
\left(\overrightarrow{\Phi}, \vec{v}_0 \right)_ {\widehat{\Xi}^1(\Omega')}
\right|
\leq
\left\| \overrightarrow{\Phi} \right\|_{\widehat{\Xi}^1(\Omega')}
\left\| \vec{v}_0\right\|_{V_0}
\;,
\]
so that \(-\left(\overrightarrow{\Phi}, \vec{v}_0 \right)_ {\widehat{\Xi}^1(\Omega')}\) is a continuous antilinear form on \(V_0\).
Then, by the Lax- Milgram theorem, the precedent problem has one and only solution.
Therefore, the problem (20) has one and one solution \(\vec{u}_0 \in V_0\) and the auxiliary problem has one and only one solution \(\vec{u}'\) in \({\widehat{\Xi}^1(\Omega')}\).
The Equation (21) can be written
\[
\left(\vec{u}', \vec{v}_0 \right)_ {\widehat{\Xi}^1(\Omega')}=0
\quad \forall \vec{v}_0 \in V_0
\]
and the solution \(\vec{u}'\) of the auxiliary problem belongs to the orthogonal of \(V_0\) in \(\widehat{\Xi}^1(\Omega')\).
Case 3. The solution \(\vec{u}'\) of the auxiliary problem does not depend on \(\overrightarrow{\Phi}\), since \(\overrightarrow{\Phi}\) is not in the terms of the problem. We are going to use this remark for giving a estimate of
\(\left\| \vec{u}'\right\|_{\widehat{\Xi}^1(\Omega')}\).
We take, for \(\overrightarrow{\Phi}\), a continuous lifting of \(u_{n|\Sigma} \vec{n}\) in
\(\widehat{\Xi}^1(\Omega')\); we have
\[
\left\| \overrightarrow{\Phi} \right\|_{\widehat{\Xi}^1(\Omega')}
\leq
c
\left\| u_{n|\Sigma} \right\|_{H^{1/2}(\Sigma)}
\quad (c>0)
\;.
\]
We have
\[
\left|
\left(\vec{u}_0, \vec{v}_0 \right)_ {V_0}
\right|
\leq
\left\| \overrightarrow{\Phi} \right\|_{\widehat{\Xi}^1(\Omega')}
\left\| \vec{v}_0\right\|_{V_0}
\]
and then
\[
\left\| \vec{u}_0\right\|_{V_0}
\leq
\left\| \overrightarrow{\Phi} \right\|_{\widehat{\Xi}^1(\Omega')}
\]
and finally
\[
\left\| \vec{u}_0\right\|_{V_0}
\leq
c
\left\| u_{n|\Sigma} \right\|_{H^{1/2}(\Sigma)}
\]
For the solution \(\vec{u}'\) of the auxiliary problem, we have
\[
\vec{u}'=\vec{u}_0+\overrightarrow{\Phi}
\]
and then
\begin{equation}
\label{eq22}
\left\| \vec{u}'\right\|_{\widehat{\Xi}^1(\Omega')}
\leq
2c
\left\| u_{n|\Sigma} \right\|_{H^{1/2}(\Sigma)}
\,.
\end{equation}
(22)
Case 4. Finally, we study \(T_n(\vec{u}')
_{|\Sigma}\) that is in the second dynamic condition (17) of the problem. We are going to show that it can be expressed by means of \(u_{n|\Sigma}\).
The solution \(\vec{u}'\) of our problem verifies:
\[
\frac{\partial \sigma'_{ij}(\vec{u}')}{\partial x_{j}}=0
\quad \text{in} \quad \Omega'
\;.
\]
Let \( \vec{\tilde{w}}'\) an element of \(\widehat{\Xi}^1(\Omega')\).
We have, by Green's formula and
\( \vec{\tilde{w}}'_{|S}=0\) :
\[
0=- \int_{\Omega'}
\frac{\partial \sigma'_{ij}(\vec{u}')}{\partial x_{j}} \cdot \bar{\tilde{w}}_{i}
\, \mathrm d\Omega'
=
-\int_{\Sigma}
\sigma'_{ij}(\vec{u}') {n}_\text{ej} \bar{\tilde {w}}_{i} \, \mathrm d\Sigma
+ \int_{\Omega'}
\sigma'_{ij}(\vec{u}')\epsilon'_{ij}(\bar{\vec{\tilde{w}}}')
\, \mathrm d\Omega'
\;.
\]
Since the solution \(\vec{u}'\) of the initial problem
verifies \(\vec{T}_t(\vec{u}')
_{|\Sigma}=0\), the precedent equation gives:
\begin{equation}
\label{eq23}
\int_{\Omega'}
\sigma'_{ij}(\vec{u}')\epsilon'_{ij}(\bar{\vec{\tilde{w}}}')
\, \mathrm d\Omega'
=
- \int_{\Sigma}
{T}_{n}(\vec{u}')_{|\Sigma} \; \bar{\tilde{w}}'_{n|\Sigma}
\, \mathrm d\Sigma
\;, \quad \forall {\vec{\tilde{w}}}' \in \widehat{\Xi}^1(\Omega')
\;.
\end{equation}
(23)
On the other hand, if \(\vec{v}'\in \left[ \mathscr{D} (\Omega')\right]^3\), we have
\[
0=-
\left\langle
\frac{\partial \sigma'_{ij}(\vec{u}')}{\partial x_{j}}
, v'_i
\right\rangle
=
\int_{\Omega'}
\sigma'_{ij}(\vec{u}')
\frac{\partial \bar{v}'_{i}}{\partial x_{j}}
\, \mathrm d\Omega'
\]
by virtue of the definition of the distributional derivatives.
Therefore, we have
\[
\int_{\Omega'}
\sigma'_{ij}(\vec{u}')\epsilon'_{ij}(\bar{\vec{v}}')
\, \mathrm d\Omega'
=0
\quad \forall \vec{v}'\in \left[ \mathscr{D} (\Omega')\right]^3
\]
and by density
\[
\int_{\Omega'}
\sigma'_{ij}(\vec{u}')\epsilon'_{ij}(\bar{\vec{v}}')
\, \mathrm d\Omega'
=0
\quad \forall \vec{v}'\in \Xi ^1(\Omega')
\;.
\]
Now, we are going to particularize
\(\vec{\tilde{w}}'\).
Let call \(w'_{n|\Sigma}\) a function defined on \(\Sigma\) and belonging to \(H^{1/2}(\Sigma)\) and let take for \(\vec{\tilde{w}}'\) a lifting of \(w'_{n|\Sigma}\vec{n}\) in \( \widehat{\Xi} ^1(\Omega')\) (so that we have
\(\tilde{w}'_{n|\Sigma}=w'_{n|\Sigma}\)). We set
\begin{equation}
\label{eq24}
\ell(\vec{\tilde{w}}')=
\int_{\Omega'}
\sigma'_{ij}(\vec{u}')\epsilon'_{ij}(\bar{\vec{\tilde{w}}}')
\, \mathrm d\Omega'
\;.
\end{equation}
(24)
Since the difference between lifting belongs to
\( \Xi ^1(\Omega')\), the right-hand side doesn't depend on the lifting \(\vec{\tilde{w}}'\). Therefore, \(\ell\) depends on \(w'_{n|\Sigma}\).
Let choose for \(\vec{\tilde{w}}'\) a continuous lifting of \(w'_{n|\Sigma}\vec{n}\); for this lifting, we have
\[
\left\| \vec{\tilde{w}}'\right\|_{\widehat{\Xi}^1(\Omega')}
\leq
\alpha
\left\| w'_{n|\Sigma} \vec{n}\right\|_{\left(H^{1/2}(\Sigma)\right)^3}
\;, \quad (\alpha>0)
\]
and, if the components of \(\vec{n}\) are sufficiently smooth:
\[
\left\| \vec{\tilde{w}}'\right\|_{\widehat{\Xi}^1(\Omega')}
\leq
\beta
\left\| w'_{n|\Sigma}\right\|_{H^{1/2}(\Sigma)}
\;, \quad (\beta>0)
\]
But, we have
\[
\left|
\ell(\vec{\tilde{w}}')
\right|
\leq
\left\| \vec{u}'\right\|_{\widehat{\Xi}^1(\Omega')}
\cdot
\left\| \vec{\tilde{w}}'\right\|_{\widehat{\Xi}^1(\Omega')}
\]
and consequently
\begin{equation}
\label{eq25}
\left|
\ell(\vec{\tilde{w}}')
\right|
\leq
\beta
\left\| \vec{u}'\right\|_{\hat{\Xi}^1(\Omega')}
\cdot
\left\| w'_{n|\Sigma}\right\|_{H^{1/2}(\Sigma)}
\end{equation}
(25)
Then, since \(\ell\) depends on \(w'_{n|\Sigma}\), it is a continuous antilinear functional on
\(H^{1/2}(\Sigma)\), i.e an element of \(\left[H^{1/2}(\Sigma)\right]'\). Taking into account of
\(\tilde{w}'_{n|\Sigma}=w'_{n|\Sigma}\), the equation (23) can be written
\[
\int_{\Sigma}
{T}_{n}(\vec{u}')_{|\Sigma} \cdot \bar{w}'_{n|\Sigma}
\, \mathrm d\Sigma
=-\ell(\vec{\tilde{w}}')
\;,
\]
so that the normal stress \( {T}_{n}(\vec{u}')_{|\Sigma} \) can be considered as an element of
\(\left( H^{1/2}(\Sigma) \right)'\).
Therefore, we have
\[
\begin{aligned}
&
\left|
\left\langle
{T}_{n}(\vec{u}')_{|\Sigma},
w'_{n|\Sigma}
\right\rangle_{\left( H^{1/2}(\Sigma) \right)',H^{1/2}(\Sigma) }
\right|
\leq
\beta
\left\| \vec{u}'\right\|_{\hat{\Xi}^1(\Omega')}
\cdot
\left\| w'_{n|\Sigma}\right\|_{H^{1/2}(\Sigma)}
\\
&
\quad \forall w'_{n|\Sigma} \in H^{1/2}(\Sigma)\;,
\end{aligned}
\]
and then
\[
\left\|
T_n(\vec{u}')
\right\|_{\left( H^{1/2}(\Sigma) \right)'}
\leq
\beta
\left\| \vec{u}'\right\|_{\widehat{\Xi}^1(\Omega')}
\;.
\]
Using (22), we obtain finally
\[
\left\|
T_n(\vec{u}')
\right\|_{\left( H^{1/2}(\Sigma) \right)'}
\leq
\delta
\left\| u_{n|\Sigma}\right\|_{H^{1/2}(\Sigma)}
\quad (\delta=2c\beta)
\;.
\]
Consequently, there exists a continuous linear operator \(\widehat{T}\) from \(H^{1/2}(\Sigma)\) into
\(\left( H^{1/2}(\Sigma) \right)'\) such that
\begin{equation}
\label{eq26}
\widehat{T}u_{n|\Sigma}
=-
T_n(\vec{u}')_{|\Sigma}\;.
\end{equation}
(26)
So, we have expressed linearly \(T_n(\vec{u}')_{|\Sigma}\) by means of \(u_{n|\Sigma}\).
The linear operator \(\widehat{T}\) depends on the elasticity of the body.
We are going to prove that it has properties of symmetry and positivity.
We introduce the analogous problem: to find \({\vec{\tilde{u}}}' \in \widehat{\Xi}^1(\Omega')\)
verifying
\begin{equation}
\label{eq27}
-\frac{\partial \sigma'_{ij}(\vec{\tilde{u}}')}{\partial x_{j}}=0
\; \text{in} \; \Omega'
\; ; \; \vec{\tilde{u}}'_{|_{S}}=0
\; ; \; \tilde{u}'_{n|\Sigma}=\tilde{u}_{n|\Sigma}
\in H^{1/2}(\Sigma)
\; ; \; \overrightarrow{T}_t \left( \vec{u}' \right)_{|\Sigma}=0\;.
\end{equation}
(27)
In (23), we replace \(\vec{\tilde{w}}'\) by
\(\vec{\tilde{u}}'\) and we have
\[
\int_{\Omega'}
\sigma'_{ij}(\vec{u}')\epsilon'_{ij}(\bar{\vec{\tilde{u}}}')
\, \mathrm d\Omega'
=
- \int_{\Sigma}
{T}_{n}(\vec{u}')_{|\Sigma} \; \bar{\tilde{u}}'_{n|\Sigma}
\, \mathrm d\Sigma
=
\left\langle
\widehat{T}u_{n|\Sigma},
\tilde{u}'_{n|\Sigma}
\right\rangle
\]
and since \( \tilde{u}'_{n|\Sigma}= \tilde{u}_{n|\Sigma}\):
\[
\int_{\Omega'}
\sigma'_{ij}(\vec{u}')\epsilon'_{ij}(\bar{\vec{\tilde{u}}}')
\, \mathrm d\Omega'
=
\left\langle
\widehat{T}u_{n|\Sigma},
\tilde{u}_{n|\Sigma}
\right\rangle
\,.
\]
Inverting roles of \(\vec{u}'\) and \(\vec{\tilde{u}}'\), we obtain
\[
\int_{\Omega'}
\sigma'_{ij}(\vec{\tilde{u}}')\epsilon'_{ij}(\bar{\vec{u}}')
\, \mathrm d\Omega'
=
\left\langle
\widehat{T}\tilde{u}_{n|\Sigma},
{u}_{n|\Sigma}
\right\rangle
\,.
\]
By virtue of the classical symmetry of the left-hand side, we obtain the property of hermitian symmetry
\[
\left\langle
\widehat{T}u_{n|\Sigma},
\tilde{u}_{n|\Sigma}
\right\rangle
=
\overline{
\left\langle
\widehat{T}\tilde{u}_{n|\Sigma},
{u}_{n|\Sigma}
\right\rangle
}
~.
\]
Now, setting \(\vec{\tilde{u}}'=\vec{u}'\), we have
\[
\left\langle
\widehat{T}u_{n|\Sigma},
{u}_{n|\Sigma}
\right\rangle
=
\int_{\Omega'}
\sigma'_{ij}(\vec{u}')\epsilon'_{ij}(\bar{\vec{u}}')
\, \mathrm d\Omega'
=
\left\|
\vec{u}'
\right\|^{2}_{\widehat{\Xi}^1(\Omega')}
~.
\]
By virtue of a trace theorem, we have
\[
\left\| u_{n|\Sigma}\right\|_{H^{1/2}(\Sigma)}
\leq
C
\left\|
\vec{u}'
\right\|_{\widehat{\Xi}^1(\Omega')}
\quad (C>0)
~.
\]
so that we have
\[
\left\langle
\widehat{T}u_{n|\Sigma},
{u}_{n|\Sigma}
\right\rangle
\geq
C^{-2}\left\| u'_{n|\Sigma}\right\|^{2}_{H^{1/2}(\Sigma)}
\]
and, since \(u'_{n|\Sigma}=u_{n|\Sigma}\), the relation of positivity
\[
\left\langle
\widehat{T}u_{n|\Sigma},
{u}_{n|\Sigma}
\right\rangle
\geq
C^{-2}\left\| u_{n|\Sigma}\right\|^{2}_{H^{1/2}(\Sigma)}
\,.
\]
The second dynamic condition (17) can be written as:
\begin{equation}
\label{eq28}
p_{|\Sigma}=\widehat{T}u_{n|\Sigma}+\rho_{0|_\Sigma} g \, n_{3|\Sigma}\;u_{n|\Sigma}\;.
\end{equation}
(28)
So, we have reduced ou problem to a problem for a gas only:
\begin{equation}
\ddot{\vec{u}}=
\overrightarrow{\text{grad}}
\left(
\frac{c^{2}_{0}(x_3) \text{div}\left[\rho_0(x_3)\vec{u}\right]}{\rho_{0}(x_3)}
\right) \;.
\label{eq15a}
\end{equation}
(29)
\begin{equation}
\label{eq29}
-c^{2}_{0}\text{div}\left(\rho_0 \vec{u}\right)_{|\Sigma}
=\widehat{T}u_{n|\Sigma}+\rho_{0|_\Sigma} g \, n_{3|\Sigma}\;u_{n|\Sigma}\;.
\end{equation}
(30)
Afterwards, the auxiliary problem gives \(\vec{u}'\), i.e. the motion of the elastic body.
s
5. Variational formulation of the problem
We consider a field of a admissible displacements
\(\vec{\tilde{u}}(x_i)\), smooth in \(\Omega\) and such that \(\vec{\tilde{u}}=\overrightarrow{\text{grad}}\, \tilde{\varphi}\). We have
\begin{eqnarray*}
\int_\Omega \rho_{0} \ddot{\vec{u}} \cdot \bar{\vec{\tilde{u}}}
\, \mathrm d\Omega
& = &
\int_\Omega \rho_{0}
\,
\overrightarrow{\text{grad}}
\left(
\frac{c^{2}_{0} \text{div}\left(\rho_0 \vec{u}\right)}{\rho_{0}}
\right)\cdot \bar{\vec{\tilde{u}}}
\, \mathrm d\Omega
\\
& = &
\int_{\Sigma}
c^{2}_{0} \text{div}\left(\rho_0 \vec{u}
\right)
\cdot
\bar{\tilde{u}}_{n|\Sigma}
\, \mathrm d\Sigma
-\int_\Omega
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0 \vec{u}\right)
\text{div}\left(\rho_0 \bar{\vec{\tilde{u}}} \right)
\, \mathrm d\Omega
\\
\end{eqnarray*}
and then
\begin{equation}
\label{eq30}
\left.
\begin{aligned}
&
\int_\Omega \rho_{0} \ddot{\vec{u}} \cdot
\bar{\vec{\tilde{u}}}
\, \mathrm d\Omega
+
\int_\Omega
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0 \vec{u}\right)
\text{div}\left(\rho_0 \bar{\vec{\tilde{u}}} \right)
\, \mathrm d\Omega
\\
&
\quad \quad
+
\int_{\Sigma}
\left(
\widehat{T}u_{n|\Sigma}+\rho_{0|_\Sigma} g \, n_{3|\Sigma}\;u_{n|\Sigma}
\right)
\bar{\tilde{u}}_{n|\Sigma}
\, \mathrm d\Sigma
=0
\,.
\end{aligned}
\right\}
\end{equation}
(31)
Conversely, let \(\vec{u}\) a function of \(t\) with values in the field of the admissible displacements and verifying (31).
We obtain easily from (31)
\begin{equation*}
\left.
\begin{aligned}
& 0=
\int_\Omega
\rho_{0}
\left[
\ddot{\vec{u}} -\overrightarrow{\text{grad}}
\left(
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0\vec{u}\right)
\right)
\right]\cdot
\overrightarrow{\text{grad}}\, \bar{\tilde{\varphi}}
\, \mathrm d\Omega
\\
&
\quad \quad
+
\int_{\Sigma}
\left[
c^{2}_{0} \text{div}\left(\rho_0\vec{u}\right)
+
\widehat{T}u_{n|\Sigma}+\rho_{0|_\Sigma} g \, n_{3|\Sigma}\;u_{n|\Sigma}
\right]
\frac{\partial \bar{\tilde{\varphi}}}{\partial n}_{|\Sigma}
\, \mathrm d\Sigma
\end{aligned}
\right\}
\,\, \forall \vec{\tilde{u}}=\overrightarrow{\text{grad}}\, \tilde{\varphi}
\,.
\end{equation*}
or
\begin{equation}
\label{eq31}
\left.
\begin{aligned}
& 0=
\int_\Sigma
\bar{\tilde{\varphi}}
\cdot
\rho_{0}
\left[
\ddot{\vec{u}} -\overrightarrow{\text{grad}}
\left(
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0\vec{u}\right)
\right)
\right]
\cdot
\vec{n}_{|\Sigma}
\, \mathrm d\Sigma
\\
&
\quad
-
\int_{\Sigma}
\left[
c^{2}_{0} \text{div}\left(\rho_0\vec{u}\right)
+
\widehat{T}u_{n|\Sigma}+\rho_{0|_\Sigma} g \, n_{3|\Sigma}\;u_{n|\Sigma}
\right]
\frac{\partial \bar{\tilde{\varphi}}}{\partial n}_{|\Sigma}
\, \mathrm d\Sigma
\\
&
\quad
-
\int_\Omega
\text{div}
\left[
\rho_{0}
\left(
\ddot{\vec{u}} -\overrightarrow{\text{grad}}
\left(
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0\vec{u}\right)
\right)
\right)
\right]
\cdot
\bar{\tilde{\varphi}}
\, \mathrm d\Omega
\,.
\end{aligned}
\right\}
\end{equation}
(32)
Taking \(\tilde{\varphi} \in \mathscr{D} (\Omega)\) and setting
\[
\overrightarrow{\Phi}_{0}=
\rho_{0} \, \overrightarrow{\text{grad}}
\left[
\ddot{\varphi}-
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0 \, \overrightarrow{\text{grad}}\,
\varphi \right)
\right]
\,,
\]
we have
\begin{equation}
\label{eq32}
\text{div} \overrightarrow{\Phi}_0=0 \quad \text{in} \quad \Omega \,.
\end{equation}
(33)
Taking \(\tilde{\varphi}_{|\Sigma}\) arbitrary and
\(\frac{\partial {\tilde{\varphi}}}{\partial n}_{|\Sigma}=0\), we obtain
\[
\rho_{0}
\left[
\ddot{\vec{u}} -\overrightarrow{\text{grad}}
\left(
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0\vec{u}\right)
\right)
\right]
\cdot
\vec{n}=0
\quad \text{on} \quad \Sigma
\]
or
\begin{equation}
\label{eq33}
\overrightarrow{\Phi}_0
\cdot
\vec{n}=0
\quad \text{on} \quad \Sigma
\;.
\end{equation}
(34)
Finally, taking \(\frac{\partial {\tilde{\varphi}}}{\partial n}_{|\Sigma}\) arbitrary, we have
\[
c^{2}_{0} \text{div}\left(\rho_0\vec{u}\right)_{|\Sigma}
+
\widehat{T}u_{n|\Sigma}+\rho_{0|_\Sigma} g \, n_{3|\Sigma}\;u_{n|\Sigma}=0
\,,
\]
i.e the dynamic condition (30).
Since
\[
\overrightarrow{\Phi}_0=\rho_0 \, \overrightarrow{\text{grad}}\, \Psi\,, \quad \text{with}
\quad
\Psi= \ddot{\varphi}-
\frac{c^{2}_{0}}{\rho_{0}} \,
\text{div}\left(\rho_0\overrightarrow{\text{grad}}\,
\varphi \right)
\,,
\]
the Equations (33) and (34) give
\begin{equation}
\label{eq34}
\text{div}
\left(
\rho_0 \, \overrightarrow{ \text{grad}}\Psi
\right)
=0
\quad \text{in} \quad \Omega \,; \quad \frac{\partial \Psi}{\partial n}_{|\Sigma}=0
\,.
\end{equation}
(35)
This Weumann problem has for solution only \(\Psi=constant\) and consequently
\[
\ddot{\vec{u}} -\overrightarrow{\text{grad}}
\left(
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0\vec{u}\right)
\right) =0
\,.
\]
6. The problem is a classical vibration problem
Case 1. We precise the field of the admissible displacements by introducing the space \(V\):
\[
V=
\left\{
\begin{aligned}
&
\vec{\tilde{u}} \in \mathscr{L}^2(\Omega)
\overset{\text{def}}{=}\left[ L^2(\Omega) \right]^3 \;\; ;\;\;
\vec{\tilde{u}}=\overrightarrow{\text{grad}}\, \tilde{\varphi}
\;\;;\;\;
\tilde{\varphi} \in \widetilde{H}^1(\Omega)
\;\;;\;\;
\text{div}\left(\rho_0\vec{\tilde{u}}\right) \in L^2(\Omega)
;
\\
&
\frac{\partial {\tilde{\varphi}}}{\partial n}_{|\Sigma}= \tilde{u}_{n|\Sigma}
\in H^{1/2}(\Sigma)
\,.
\end{aligned}
\right\}
\,,
\]
equipped with the hilbertian norm defined by
\[
\left\|\vec{u}\right\|_{V} ^2= \int_{\Omega} \rho_0 \, \left|\vec{u}\right|^2 \, \mathrm
d\Omega
+
\int_{\Omega} \left|
\text{div}\left(\rho_0 \vec{u}\right)
\right|^2 \, \mathrm d\Omega
+\left\|{u}_{n|\Sigma} \right\|_{H^{1/2}(\Sigma)}^2
\,,
\]
and the space \(H\) completion of \(V\) for the norm associated to the scalar product
\[
\left(
\vec{u},\vec{\tilde{u}}
\right)_H
=
\int_\Omega \rho_{0} {\vec{u}} \cdot \bar{\vec{\tilde{u}}}
\, \mathrm d\Omega
\,.
\]
Setting
\[
a\left(
\vec{u},\vec{\tilde{u}}
\right)
=
\int_\Omega
\frac{c^{2}_{0}}{\rho_{0}}
\text{div}\left(\rho_0 \vec{u}\right)
\text{div}\left(\rho_0 \bar{\vec{\tilde{u}}} \right)
\, \mathrm d\Omega
+
\int_{\Sigma}
\left(
\widehat{T}u_{n|\Sigma}+\rho_{0|_\Sigma} g \, n_{3|\Sigma}\;u_{n|\Sigma}
\right)
\bar{\tilde{u}}_{n|\Sigma}
\, \mathrm d\Sigma
\,,
\]
we obtain the precise variational formulation of the problem. To find \(\vec{u} (\cdot) \in V \) such that
\[
\left(
\ddot{\vec{u}},\vec{\tilde{u}}
\right)_H
+
a\left(
\vec{u},\vec{\tilde{u}}
\right)
=0
\quad \forall \vec{\tilde{u}} \in V \,.
\]
Case 2. Let us study the hermitian sesquilinear form
\[
\mathscr{C}
\left(
u_{n|\Sigma}
,
{\tilde{u}}_{n|\Sigma}
\right)
\overset{\text{def}}{=}
\int_{\Sigma}
\left(
\widehat{T}u_{n|\Sigma}+\rho_{0|_\Sigma} g \, n_{3|\Sigma}\;u_{n|\Sigma}
\right)
\bar{\tilde{u}}_{n|\Sigma}
\, \mathrm d\Sigma
\]
\(\mathscr{C}\) is continuous on \(H^{1/2}(\Sigma)\times H^{1/2}(\Sigma)\) and we have:
\[
\mathscr{C}
\left(
u_{n|\Sigma}
,
{u}_{n|\Sigma}
\right)
\geq
\left(
C^{-2}-\text{max}\rho_{0|\Sigma}\,g
\right)
\left\|{u}_{n|\Sigma} \right\|_{H^{1/2}(\Sigma)}^2
\,.
\]
In the following, we suppose that \(\mathscr{C}\) is coercive, i.e
\[
C^{-2}-\text{max}\rho_{0|\Sigma}\,g>0
\]
(for example, if \(\text{max}\rho_{0|\Sigma}\) is sufficiently
small).
Then, \(\left[ \mathscr{C}
\left(
u_{n|\Sigma}
,
{u}_{n|\Sigma}
\right)
\right]^{1/2}\)
defines on \(H^{1/2}(\Sigma)\) a norm that is equivalent to the classical norm of \(H^{1/2}(\Sigma)\).
Case 3.
In order to prove that the problem is a classical vibration problem, we use the method that is introduced in [
7].
We must prove that
- a)
\(
\left[ a\left(
\vec{u},\vec{u}
\right)
\right]^{1/2}\)
defines on \(V\) a norm equivalent to
\(\left\|
\vec{u}
\right\|_{V}\).
- b)
The imbedding \(V\subset H\), obviously dense and continuous, hence compact.
We omit the proof that is strictly identical to the proof in [7], p66-68.
Therefore there exists a denumerable infinity of positive real eigenvalues \(\omega^2_p\):
\[
0< \omega^2_1 \leq \omega^2_2 \leq \cdots \leq \omega^2_p\leq \cdots \,;\,\, \omega^2_p
\rightarrow + \infty \,\, \text{when}\,\, p \rightarrow +\infty
\,.
\]
The eigenelements
\(\left\{ \vec{u}_p\right\}\) form an orthonormal basis in \(H\) and an orthogonal basis in \(V\) equipped with the scalar product
\(\left(
\vec{u},\vec{\tilde{u}}
\right)_V\).
To each eigenmotion \(\left\{ \vec{u}_p\right\}\) of the gas corresponds an eigenmotion \(\left\{ \vec{u}'_p\right\}\) of the elastic body verifying
\[
\left\| \vec{u}'_p\right\|_{\widehat{\Xi}^1(\Omega')}
\leq
2c
\left\| u_{np|\Sigma} \right\|_{H^{1/2}(\Sigma)}.
\]
Author Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Competing Interests
The author(s) do not have any competing interests in the manuscript.