Open Journal of Mathematical Sciences
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2021.0144
Generalized orthopair fuzzy sets based on Hamacher T-norm and T-conorm
I. Silambarasan
Department of Mathematics, Annamalai University, Annamalainagar-608002, Tamilnadu, India.; sksimbuking@gmail.com
Abstract
Keywords:
1. Introduction
Zadeh fuzzy set (FS) has acquired greater attention by researchers in a wide range of scientific areas, including management sciences, robotics, decision theory and many other disciplines [1]. FSs were further generalized to intuitionistic fuzzy sets (IFSs) by Atanassov [2] in 1983. An IFS is distinguished by a truth-membership (T) and falsity-membership (F) satisfying the condition that the sum of both membership degrees should not exceed one. IF values play an important role in both theoretical and practical progress of IFSs. Applications of IFSs appear in various fields, including medical diagnosis, optimization problems, and decision-making. Recently, Liu et al., [3] introduced and explored various types of centroid transformations of IF values. However, in many practical decision-making problems, the sum of truth-membership and falsity-membership may not be less than one, but the sum of their squares may be less than one. To handle such types of difficulties, Yager [4,5] introduced the novel concept of Pythagorean fuzzy sets (PFSs), which is the generalization of IFSs.
Compensating the constraint that the summation of both membership degrees does not exceed one and that the sum of squares of the membership degrees should not be greater than one makes PFSs more powerful, generalizable, and effective. Zhang and Xu [6] studied various binary operations over PFS and also proposed a decision making algorithm based on PFS. Zeng et al., [7] developed a hybrid method for Pythagorean fuzzy multiple-criteria decision making. Garg [8] defined the new generalized Pythagorean fuzzy information aggregation by using Einstein Operations. A generalized union and a generalized intersection on PFSs can be constructed from a general t-norm and t-conorm. Hamacher operations [9], including Hamacher product and Hamacher sum, are good alternatives to the algebraic product and algebraic sum, respectively. Gao [10] proposed some Pythagorean fuzzy Hamacher prioritized aggregation operators in MADM. In recent years, many researchers studied the Hamacher aggregation operators and their applications [11,12,13,14].
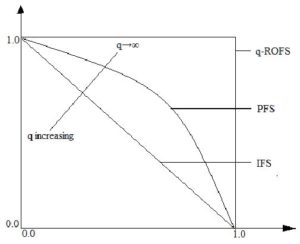
PFSs can deal with various real-life problems more effectively, still there are cases that cannot be handled using PFSs. Take an example: The truth-membership and falsity-membership values suggested by a decision-maker are 0.8 and 0.9, respectively. Then, the problem can never be handled by means of PFSs, as \(\left(0.8\right)^2+\left(0.9\right)^2=1.45> 1\). In order to deal with such types of cases, Yager [15] submitted the idea of q-rung orthopair fuzzy sets (q-ROFSs). A q-ROFS is represented by means of two membership degrees; one is the truth and the other is falsity, with the characteristic that the summation of the \(q^{th}\) power of truth-membership and the \(q^{th}\) power of falsity-membership should not be greater than one. Thus, q-ROFSs extend the concepts of IFSs and PFSs, so that the uncertain information can be dealt with in a widened range. We can see that the IFS and PFS are special cases of q-ROFS. As q-rung increases, the range of processing fuzzy information increases. The acceptable space for different types of fuzzy numbers is shown in the Figure 1. IFS, PFS, and q-ROFS are abbreviations of intuitionistic fuzzy number, Pythagorean fuzzy number, and q-rung orthopair fuzzy number, respectively. Therefore, it can be seen that q-ROFS has stronger capability in dealing with uncertain information than the IFS and PFS.
Figure 1. Comparison of grades space of IFS, PFS, and q-ROFS
After that, Liu and Wang [16] developed and applied certain simple weighted operators to aggregate q-ROFSs in decision-making. This set can adjust the range of indication of decision data by changing the parameter \(q, ~q\geq1\). Wei et al., [17] defined q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision-making.
In this paper, we propose the concepts of q-rung orthopair fuzzy Hamacher operations and investigates their desirable properties. This paper is arranged as follows; In Section 2, some basic concepts of q-rung orthopair fuzzy sets and Hamacher operations. In Section 3, we define the Hamacher operations of q-rung orthopair fuzzy sets and studied some desirable properties. In Section 4, on complement of q-rung orthopair fuzzy sets are studied. In Section 5, we constructed Hamacher scalar multiplication \(({n._{h}}A)\) and Hamacher exponentiation \((A^{\wedge_{h}n})\) operations of q-rung orthopair fuzzy set \(A\) and investigated their algebraic properties. In Section 6, some properties of necessity and possibility operators on q-rung orthopair fuzzy sets are proved. In Section 7, comparison analysis of the proposed model with IF and PF models. Section 8 concludes the paper and some future directions are presented in Section 9.
2. Preliminaries
In this section, some basic concepts of q-rung orthopair fuzzy sets and Hamacher operations.Definition 1. [15] A q-rung orthopair fuzzy set \(A\) on a universe \(X\) is an object of the form \(A=\left\{\left(x, \mu_A(x),\nu_A(x)\right)|x\in X\right\}\), where \(\mu_A(x)\in[0,1]\) is called the degree of membership of \(x\) in \(A\), \(\nu_A(x)\in[0,1]\) is called the degree of non-membership of \(x\) in \(A\), and where \(\mu_A(x)\) and \(\nu_A(x)\) satisfy the following condition; \[0\leq \mu^q_A(x)+\nu^q_A(x)\leq 1 (q\geq 1)\ \ \ \text{for all}\ \ \ x\in X.\]
2.1. Hamacher operations
T-norm and T-conorm are an important notion in the intuitionistic fuzzy set theory, which is used to define a generalized union and intersection of intuitionistic fuzzy sets [18]. Roychowdhury and Wang [19] gave the definition and conditions of \(t-norm\) and \(t-conorm\). Deschrijver and Kerre [20] introduced and analyzed the properties of a generalized union and a generalized intersection of intuitionistic fuzzy sets using the general triangular norm \((t-norm)\) and triangular conorm \((t-conorm)\). Hamacher [9] proposed a more generalized \(t-norm\) and \(t-conorm\). Hamacher operation includes the Hamacher product and Hamacher sum, which are examples of \(t-norms\) and \(t-conorms\), respectively. Hamacher product \(\odot\) is a \(t-norm\) and Hamacher sum \(\oplus\) is a \(t-conorm\) and are defined as; \begin{align*} T(a,b)&=a\odot b=\dfrac{ab}{\gamma+(1-\gamma)(a+b-ab)},\gamma=0,\\ T^*(a,b)&=a\oplus b=\dfrac{a+b-ab-(1-\gamma)ab}{1-(1-\gamma)ab},\gamma=0, \end{align*} respectively. Especially, when \(\gamma=1,\) then Hamacher t-norm and t-conorm will reduce to \begin{align*} T(a,b)&=a\odot b=ab, \\ T^*(a,b)&=a\oplus b=a+b-ab, \end{align*} which are the algebraic t-norm and t-conorm respectively. When \(\gamma=2,\) then Hamacher t-norm and t-conorm will reduce to \begin{align*} T(a,b)&=a\odot b=\dfrac{ab}{1+(1-a)(1-b)}, \\ T^*(a,b)&=a\oplus b=\dfrac{a+b}{1+ab}, \end{align*} which are called the Einstin t-norm and t-conorm respectively.3. Hamacher operations of q-rung orthopair fuzzy sets
In this section, we define the Hamacher operations of q-rung orthopair fuzzy sets and analyze some desirable properties.Definition 2. Let \(A=\left\{\left( x, \mu_A(x),\nu_A(x)\right) | x\in X \right\}\) and \(B=\left\{\left( x, \mu_B(x),\nu_B(x)\right) | x\in X \right\}\) be any two q-rung orthopair fuzzy sets, then we have
- (i) The Hamacher sum of \(A\) and \(B\) is defined by \[A\boxplus_{h} B= \begin{cases}\left( 1,0\right),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ \text{if}~ \left( \mu_A(x),\nu_A(x)\right)=\left( 1,0\right) ,\left( \mu_B(x),\nu_B(x)\right)=\left( 1,0\right)\\[4mm] \left( x, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\right),~ \text{otherwise}, \end{cases}\] for all \(x\in X~ (q\geq 1)\), and
- (ii) The Hamacher product of \(A\) and \(B\) is defined by \[A\boxtimes_{h} B= \begin{cases}\left( 0,1\right),~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\text{if}~ \left( \mu_A(x),\nu_A(x)\right)=\left( 0,1\right),\left( \mu_B(x),\nu_B(x)\right)=\left( 0,1\right) \\[4mm] \left( x, \left(\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}~~\right), ~ \text{otherwise}, \end{cases}\] for all \(x\in X~ (q\geq 1)\).
Lemma 1. For any two real numbers \(a,b\in [0,1]\), the following inequality holds; \[\left(\dfrac{a^qb^q}{a^q+b^q-a^qb^q}\right)^{1/q}\leq \left(\dfrac{a^q+b^q-2a^qb^q}{1-a^qb^q}\right)^{1/q}.\]
Lemma 2. If \(A\subseteq B\), then for any three real numbers \(a,b,c\in[0,1]\), the following inequalities hold;
- (i) \(\left(\dfrac{a^qc^q}{a^q+c^q-a^qc^q}\right)^{1/q}\leq \left(\dfrac{b^qc^q}{b^q+c^q-b^qc^q}\right)^{1/q},\)
- (ii) \(\left(\dfrac{a^q+c^q-2a^qc^q}{1-a^qc^q}\right)^{1/q}\leq \left(\dfrac{b^q+c^q-2b^qc^q}{1-b^qc^q}\right)^{1/q}.\)
Theorem 1. If \( A, B \in q-ROFS(X)\), then \(A\boxtimes_{h} B\subseteq A\boxplus_{h} B\).
Proof. By using Lemma (1), we have \begin{align*} \left(\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}&\leq \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q},\end{align*} and \begin{align*} \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q} \geq \left(\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\end{align*} for all \(x\in X\).
By Definition (2), it follows that \(A\boxtimes_{h} B\subseteq A\boxplus_{h} B\).
Theorem 2. If \(A\in q-ROFS(X)\), then
- (i) \( A\boxplus_{h}A\supseteq A,\)
- (ii) \( A\boxtimes_{h}A\subseteq A\).
Proof.
- (i) \begin{align*} A\boxplus_{h} A &=\left\{\left.\left( x, \left(\dfrac{2\mu^q_A(x)-2\mu^q_A(x)}{1-\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{2\nu^q_A(x)-\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{2\mu^q_A(x)}{1+\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{2-\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &\geq \left\{\left.x,\mu^q_A(x),\nu^q_A(x)\right| x\in X \right\}\ \ \ \left(\text{since}\ \ \mu^q_A(x)\leq \dfrac{2\mu^q_A(x)}{1+\mu^q_A(x)}\ \ \text{and} \ \ \nu^q_A(x)\geq \dfrac{\nu^q_A(x)}{2-\nu^q_A(x)}\right)\\ &\geq \left\{\left.x,\mu_A(x),\nu_A(x)\right| x\in X \right\}\ \ \ \left(\text{for all}\ \ x \in X\right)\\ &\geq A.\end{align*} Hence, \(A\boxplus_{h}A\supseteq A\).
- (ii) It can be proved similarly.
Theorem 3. If \( A, B, C \in q-ROFS(X)\), then
- (i) \( A\boxplus_{h} B=B\boxplus_{h} A,\)
- (ii) \( (A\boxplus_{h} B)\boxplus_{h} C=A\boxplus_{h}(B\boxplus_{h} C),\)
- (iii) \(A\boxtimes_{h} B=B\boxtimes_{h} A,\)
- (iv) \((A\boxtimes_{h} B)\boxtimes_{h} C=A\boxtimes_{h}(B\boxtimes_{h} C)\).
Theorem 4. If \(A\in q-ROFS(X)\), then
- (i) \(A\boxplus_{h}\emptyset = \emptyset \boxplus_{h} A=A,\)
- (ii) \(A\boxtimes_{h} X=X\boxtimes_{h} A=A,\)
- (iii) \(A\boxplus_{h} X=X,\)
- (iv) \(A\boxtimes_{h} \emptyset=\emptyset\).
Theorem 5. For \( A, B \in q-ROFS(X)\), if \(A\subseteq B\), then \(A\boxtimes_{h} C\subseteq B\boxtimes_{h} C\).
Proof. Let \(\mu_A(x)\leq \mu_B(x)\) and \(\nu_A(x)\geq \nu_B(x)\) for all \(x \in X\). By using Lemma (2), we have \[\left(\dfrac{\mu^q_A(x)\mu^q_C(x)}{\mu^q_A(x)+\mu^q_C(x)-\mu^q_A(x)\mu^q_C(x)}\right)^{1/q}\leq \left(\dfrac{\mu^q_B(x)\mu^q_C(x)}{\mu^q_B(x)+\mu^q_C(x)-\mu^q_B(x)\mu^q_C(x)}\right)^{1/q}\] and \[\left(\dfrac{\nu^q_B(x)\nu^q_C(x)}{\nu^q_B(x)+\nu^q_C(x)-\nu^q_B(x)\nu^q_C(x)}\right)^{1/q}\geq \left(\dfrac{\nu^q_A(x)\nu^q_C(x)}{\nu^q_A(x)+\nu^q_C(x)-\nu^q_A(x)\nu^q_C(x)}\right)^{1/q}\] for all \(x \in X\). Therefore, \(A\boxtimes_{h} C\subseteq B\boxtimes_{h} C.\)
Theorem 6. For \( A, B \in q-ROFS(X)\), if \(A\subseteq B\), then \(A\boxplus_{h} C\subseteq B\boxplus_{h} C\).
Proof. Let \(\mu_A(x)\leq \mu_B(x)\) and \(\nu_A(x)\geq \nu_B(x)\) for all \(x \in X\). By using Lemma (2), we have \[\left(\dfrac{\mu^q_A(x)+\mu^q_C(x)-2\mu^q_A(x)\mu^q_C(x)}{1-\mu^q_A(x)\mu^q_C(x)}\right)^{1/q}\leq \left(\dfrac{\mu^q_B(x)+\mu^q_C(x)-2\mu^q_B(x)\mu^q_C(x)}{1-\mu^q_B(x)\mu^q_C(x)}\right)^{1/q}\] and \[\left(\dfrac{\nu^q_B(x)+\nu^q_C(x)-2\nu^q_B(x)\nu^q_C(x)}{1-\nu^q_B(x)\nu^q_C(x)}\right)^{1/q}\geq \left(\dfrac{\nu^q_A(x)+\nu^q_C(x)-2\nu^q_A(x)\nu^q_C(x)}{1-\nu^q_A(x)\nu^q_C(x)}\right)^{1/q}.\] Therefore, \(A\boxplus_{h} C\subseteq B\boxplus_{h} C.\)
Theorem 7. If \( A, B \in q-ROFS(X)\), then
- (i) \((A\cap B) \boxplus_{h} (A\cup B)=A\boxplus_{h} B,\)
- (ii) \((A\cap B)\boxtimes_{h} (A\cup B)=A\boxtimes_{h} B \).
Proof. (i) \begin{align*}(A&\cap B)\boxplus_{h}(A\cup B)\\ &=\left( \min\left\{\mu_A(x),\mu_B(x)\right\},\max\left\{\nu_A(x),\nu_B(x)\right\}\right) \boxplus_{h}\left( \max\left\{\mu_A(x),\mu_B(x)\right\},\min\left\{\nu_A(x),\nu_B(x)\right\}\right)\\ &=\left[ \left(\dfrac{\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}+\max\left\{\mu^q_A(x),\mu^q_B(x)\right\}-2\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\max\left\{\mu^q_A(x),\mu^q_B(x)\right\}}{1-\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\max\left\{\mu^q_A(x),\mu^q_B(x)\right\}}\right)^{1/q} , \right.\\ &\;\;\;\;\left.\left(\dfrac{\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\min\left\{\nu^q_A(x),\nu^q_B(x)\right\}}{\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}+\min\left\{\nu^q_A(x),\nu^q_B(x)\right\}-\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\min\left\{\nu^q_A(x),\nu^q_B(x)\right\}}\right)^{1/q}\right]\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x) \mu^q_B(x)}{1-\mu^q_A(x) \mu^q_B(x)}\right)^{1/q},\left(\dfrac{\nu^q_A(x) \nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x) \nu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}=A\boxplus_{h} B.\end{align*} (ii) It can be proved similarly.
4. On complement of q-rung orthopair fuzzy sets
In this section, the complement of a q-rung orthopair fuzzy set is used to analyze the complementing nature of any system. Using the following results, we can study the complementing nature of a system with the help of the original q-rung orthopair fuzzy set. The operator complement obey De Morgan's law for the operations \(\boxplus_{h}\) and \(\boxtimes_{h}\). This is established in the following theorem.Theorem 8. If \( A, B \in q-ROFS(X)\), then
- (i) \((A\boxplus_{h} B)^C=A^C\boxtimes_{h} B^C,\)
- (ii) \((A\boxtimes_{h} B)^C=A^C\boxplus_{h} B^C,\)
- (iii) \((A\boxplus_{h} B)^C\subseteq A^C\boxplus_{h} B^C,\)
- (iv) \((A\boxtimes_{h} B)^C\supseteq A^C\boxtimes_{h} B^C,\)
- (v) \((A^C\boxtimes_{h} B^C)^C=A\boxplus_{h} B,\)
- (vi) \((A^C\boxplus_{h} B^C)^C=A\boxtimes_{h} B\).
Proof. \begin{align*} \text{(i).}\;\;\;A^C\boxtimes_{h} B^C &=\left\{\left.\left( x, \left(\dfrac{\nu^q_A(x) \nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x) \nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x) \mu^q_B(x)}{1-\mu^q_A(x) \mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=(A\boxplus_{h} B)^C. \end{align*} \begin{align*} \text{(ii).}\;\;\;A^C\boxplus_{h} B^C&=\left\{\left.\left( x, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x) \nu^q_B(x)}{1-\nu^q_A(x) \nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\mu^q_A(x) \mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x) \mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=(A\boxtimes_{h} B)^C.\end{align*} \begin{align*} \text{(iii).}\;\;\;(A\boxplus_{h} B)^C&= \left\{\left.\left( x, \left(\dfrac{\nu^q_A(x) \nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x) \nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x) \mu^q_B(x)}{1-\mu^q_A(x) \mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ A^C\boxplus_{h} B^C&=\left\{\left.\left( x, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x) \nu^q_B(x)}{1-\nu^q_A(x) \nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\mu^q_A(x) \mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x) \mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}.\end{align*} By Lemma (1), we have \[\left(\dfrac{\nu^q_A(x) \nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x) \nu^q_B(x)}\right)^{1/q}\leq \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x) \nu^q_B(x)}{1-\nu^q_A(x) \nu^q_B(x)}\right)^{1/q}\] and \[\left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x) \mu^q_B(x)}{1-\mu^q_A(x) \mu^q_B(x)}\right)^{1/q} \geq \left(\dfrac{\mu^q_A(x) \mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x) \mu^q_B(x)}\right)^{1/q}\] for all \(x\in X\). Hence \((A\boxplus_{h} B)^C\subseteq A^C\boxplus_{h} B^C\). Similarly, we can prove (iv), (v) and (vi).
5. Scalar multiplication and Exponentiation operations on q-rung orthopair fuzzy sets
We defined the following operations over Hamacher operations on q-ROFSs. In this section, we construct Hamacher scalar multiplication \(({n._{h}}A)\) and Hamacher exponentiation \((A^{\cap_{h}n})\) operations on q-rung orthopair fuzzy set \(A\) and investigate their algebraic properties.Based on the Definition (2), Hamacher sum and Hamacher product over two q-ROFSs \(A\) and \(B\) are further indicated as the following operations.
Theorem 9. If \(n\) is any positive number and \(A\) is a q-ROFS of \(X\), then the Hamacher scalar multiplication operation \((._{h})\) is a mapping from \(R^+ \times X\) to \(X\):
Proof. Mathematical induction can be used to prove that the Equation (1) holds for all positive integer \(n\). The Equation (1) is called P(n). Using Definition 2(i) of Hamacher sum (\(A\boxplus_{h} B\)), we have \begin{align*} A._{h} A&= \left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)+\mu^q_A(x)-2\mu^q_A(x)\mu^q_A(x)}{1-\mu^q_A(x)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{\nu^q_A(x)\nu^q_A(x)}{\nu^q_A(x)+\nu^q_A(x)-\nu^q_A(x)\nu^q_A(x)}\right)^{1/q} \hspace{0.2cm}\right) \right| x\in X \right\},\\ &=\left\{\left.\left( x, \left(\dfrac{2\mu^q_A(x)-2a^q_{ij}}{1-a^q_{ij}}\right)^{1/q}, \left(\dfrac{\nu^q_{\mu^q_A(x)}}{2\nu^q_A(x)-\nu^q_{\mu^q_A(x)}}\right)^{1/q} \hspace{0.2cm}\right) \right| x\in X \right\} ,\\ &=\left\{\left.\left( x, \left(\dfrac{2\mu^q_A(x)(1-\mu^q_A(x))}{1-a^6_{ij}}\right)^{1/q}, \left(\dfrac{\nu^q_{\mu^q_A(x)}}{\nu^q_A(x)(2-\nu^q_A(x))}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}, \\ &=\left\{\left.\left( x, \left(\dfrac{2\mu^q_A(x)(1-\mu^q_A(x))}{(1-\mu^q_A(x))(1+\mu^q_A(x))}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{(2-\nu^q_A(x))}\right)^{1/q} \hspace{0.2cm}\right) \right| x\in X \right\}, \\ &=\left\{\left.\left( x, \left(\dfrac{2\mu^q_A(x)}{1+\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{(2-\nu^q_A(x))}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\},\\ 2._{h} A&=\left\{\left.\left( x, \left(\dfrac{2\mu^q_A(x)}{1+(2-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{2-(2-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}.\end{align*} Since \(\mu^q_A(x)=(2-1)\mu^q_A(x),\) we have \begin{align*} n._{h} A&=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q} \hspace{0.2cm}\right) \right| x\in X \right\}.\end{align*} Hence P(n) holds.
Suppose that Equation (1) holds for \(n=m\), i.e.,
\[ m._{h} A=\underbrace{A\boxplus_{h}...\boxplus_{h} A}_{m}=\left\{\left.\left( x, \left(\dfrac{m\mu^q_A(x)}{1+(m-1)\mu^q_A(x)}\right)^{1/q} , \left(\dfrac{\nu^q_A(x)}{m-(m-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}.\] Then, \((m+1)._{h}A=((m._{h}A)\boxplus_{h} A)\) \begin{align*}&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;=\left[ \left(\dfrac{\dfrac{m\mu^q_A(x)}{1+(m-1)\mu^q_A(x)}+\mu^q_A(x)-2\dfrac{m\mu^q_A(x)}{1+(m-1)\mu^q_A(x)}.\mu^q_A(x)}{1-\dfrac{m\mu^q_A(x)}{1+(m-1)\mu^q_A(x)}.\mu^q_A(x)}\right)^{1/q},\right.\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\;\;\;\; \left.\left(\dfrac{\dfrac{\nu^q_A(x)}{m-(m-1)\nu^q_A(x)}.\nu^q_A(x)}{\dfrac{\nu^q_A(x)}{m-(m-1)\nu^q_A(x)}+\nu^q_A(x)-\dfrac{\nu^q_A(x)}{m-(m-1)\nu^q_A(x)}.\nu^q_A(x)}\right)^{1/q}\right]\end{align*} \begin{align*} &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)(m+1)(1-\mu^q_A(x))}{(1+m\mu^q_A(x))(1-\mu^q_A(x))}\right)^{1/q}, \left(\dfrac{(\nu^q_A(x))^2}{\nu^q_A(x)(m+1-m\nu^q_A(x))}\right)^{1/q} \hspace{0.2cm}\right) \right| x\in X \right\} \\ &=\left\{\left.\left( x, \left(\dfrac{(m+1)\mu^q_A(x)}{1+m\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{m+1-m\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\} \\ &=\left\{\left.\left( x, \left(\dfrac{(m+1)\mu^q_A(x)}{1+[(m+1)-1]\mu^q_A(x)}\right)^{1/q} , \left(\dfrac{\nu^q_A(x)}{m+1-[(m+1)-1]\nu^q_A(x)}\right)^{1/q} \hspace{0.2cm}\right) \right| x\in X \right\}.\end{align*} So, when \(n=m+1\), \[n._{h} A=\underbrace{A\boxplus_{h}...\boxplus_{h} A}_{n}=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q} \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}, \] also holds. Hence, using the induction hypothesis, P(n) holds for any positive integer \(n\).Theorem 10. If \(n\) is any positive integer and \(A\) is a q-ROFS of \(X\), then the Hamacher exponentiation operation \((\wedge_{h})\) is a mapping from \(Z^+ \times X\) to \(X\):
Proof. Mathematical induction can be used to prove that the Equation (2) holds for all positive integer \(n\). The Equation (2) is called P(n). Using Definition 2(ii) of Hamacher product (\(A\boxtimes_{h} B\)), we have \begin{align*} {A^{\wedge_{h}}}^A &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)\mu^q_A(x)}{\mu^q_A(x)+\mu^q_A(x)-\mu^q_A(x)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)+\nu^q_A(x)-2\nu^q_A(x)\nu^q_A(x)}{1-\nu^q_A(x)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_{\mu^q_A(x)}}{2\mu^q_A(x)-\mu^q_{\mu^q_A(x)}}\right)^{1/q},\left(\dfrac{2\nu^q_A(x)-2\nu^q_{\mu^q_A(x)}}{1-\nu^q_{\mu^q_A(x)}}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_{\mu^q_A(x)}}{\mu^q_A(x)(2-\mu^q_A(x))}\right)^{1/q},\left(\dfrac{2\nu^q_A(x)(1-\nu^q_A(x))}{1-\nu^6_{\mu^q_A(x)}}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{(2-\mu^q_A(x))}\right)^{1/q},\left(\dfrac{2\nu^q_A(x)(1-\nu^q_A(x))}{(1-\nu^q_A(x))(1+\nu^q_A(x))}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{(2-\mu^q_A(x))}\right)^{1/q},\left(\dfrac{2\nu^q_A(x)}{1+\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\},\\ {A^{\wedge_{h}}}^q&=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{2-(2-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{2\nu^q_A(x)}{1+(2-1)\nu^q_A(x)}\right)^{1/q} \hspace{0.2cm}\right) \right| x\in X \right\}. \end{align*} Since \(\mu^q_A(x)=(2-1)\mu^q_A(x)\), we have \begin{align*}{A^{\wedge_{h}}}^n=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \hspace{0.2cm}\right) \right| x\in X \right\}.\end{align*} Hence P(n) holds.
Suppose that the Equation (2) holds for \(n=m\), i. e.,
\begin{align*}{A^{\wedge_{h}}}^m=\overbrace{A\boxtimes_{h}...\boxtimes_{h} A}^{m}=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{m-(m-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{m\nu^q_A(x)}{1+(m-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\},\end{align*} so, when \(n=m+1\), \begin{align*}{A^{\wedge_{h}}}^{m+1}&=\left\{\left.\left( x, \left(\dfrac{{\mu_A(x)}^2}{m+1-[(m+1)-1]{\mu_A(x)}^2}\right)^{1/q},\left(\dfrac{(m+1)\nu^q_A(x)}{1+[(m+1)-1]\nu^q_A(x)}\right)^{1/q} \hspace{0.2cm} \right) \right| x\in X \right\},\\ {A^{\wedge_{h}}}^n&=\overbrace{A\boxtimes_{h}...\boxtimes_{h} A}^{n}=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm} \right) \right| x\in X \right\}\end{align*} also holds. Hence, using the induction hypothesis, P(n) holds for any positive integer \(n\).Next, we prove the result of \(({n._{h}}A)\) and \((A^{\wedge_{h}n})\) are also FFMs.
Theorem 11. For any q-ROFS \(A\) and for any positive integer \(n\), \(({n._{h}}A)\) and \((A^{\wedge_{h}n})\) are q-ROFSs.
Proof. Since \( 0\leq \mu^q_A(x) \leq 1,\) \(0\leq \nu^q_A(x) \leq 1,\) \( 0\leq \mu^q_A(x)+\nu^q_A(x) \leq 1,\) and \(n>1\), we have \( (n-1)\mu^q_A(x)>-1,\) \(1+(n-1)\mu^q_A(x)> 0,\) and \(n-(n-1)\nu^q_A(x)=(1-\nu^q_A(x))n+\nu^q_A(x)> \nu^q_A(x)\geq 0.\) Then, it is easy to get \[ \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\geq 0,\ \ \ \text{and}\ \ \ \left (\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\geq 0.\] Considering \(1+(n-1)\mu^q_A(x)=n\mu^q_A(x)+1-\mu^q_A(x)\geq n\mu^q_A(x),\) and \(n-(n-1)\nu^q_A(x)=\nu^q_A(x)+n(1-\nu^q_A(x))\geq \nu^q_A(x),\) we get \[\left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\leq 1,\ \ \ \text{and}\ \ \ \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\leq 1.\] For \(\mu^q_A(x)+\nu^q_A(x)\leq 1,\) and \(0\leq \nu^q_A(x)\leq 1-\mu^q_A(x)\), we get \begin{align*} \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q} &+\left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}=\left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q} +\left(\dfrac{1}{\dfrac{n}{\nu^q_A(x)}-(n-1)}\right)^{1/q}\\ &\leq \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q} +\left(\dfrac{1}{\dfrac{n}{1-\mu^q_A(x)}-(n-1)}\right)^{1/q}=1.\end{align*} Thus, we have \[0\leq \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\leq 1,\ \ \ \text{and}\ \ \ 0\leq \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\leq 1,\] which implies that \[\left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q} +\left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\leq 1.\] Similarly, we have \[0\leq \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}\leq 1,\ \ \ \text{and} \ \ \ 0\leq \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q}\leq 1,\] which implies that \[ \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}+\left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q}\leq 1.\] Hence, \(({n._{h}})A\) and \((A^{\wedge_{h}n})\) are q-ROFSs.
Theorem 12. If \(A, B \in q-ROFS(X)\), then for any positive integers \(n,n_{1},n_{2}\), we have
- (i) \({n_{1}._{h}}A\boxplus_{h} {n_{2}._{h}}A=(n_{1}+n_{2})._{h} A,\)
- (ii) \(({n._{h}}A)\boxplus_{h} ({n._{h}}B)={n._{h}}(A\boxplus_{h} B),\)
- (iii) \(A^{\wedge_{h}n_{1}}\boxtimes_{h}A^{\wedge_{h}n_{2}}=A^{\wedge_{h}(n_{1}+n_{2})},\)
- (iv) \(A^{\wedge_{h}n} \boxtimes_{h} B^{\wedge_{h}n}=(A\boxtimes_{h} B)^{\wedge_{h}n},\)
- (v) \({n_{2}._{h}}({n_{1}._{h}}A)=(n_{1}n_{2})._{h} A,\)
- (vi) \( {({A^{\wedge_{h}}}^{n_{1}})^{\wedge_{h}}}^{n_{2}}={A^{\wedge_{h}}}^{(n_{1}n_{2})}.\)
Proof. We shall prove (i), (ii), (v) and (iii), (iv), (vi) can be proved analogously.
(i) By Equations (1) and (2), we have \begin{align*}n_{1}._{h} A&=\left\{\left.\left( x, \left(\dfrac{n_{1}\mu^q_A(x)}{1+(n_{1}-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n_{1}-(n_{1}-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}=\left( \mu_B(x),\nu_B(x)\right),\end{align*} and \begin{align*} n_{2}._{h} A&=\left\{\left.\left( x, \left(\dfrac{n_{2}\mu^q_A(x)}{1+(n_{2}-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n_{2}-(n_{2}-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}=\left( \mu_C(x),\nu_C(x)\right).\end{align*} Since \(B\boxplus_{h} C=(n_{1}._{h} A)\boxplus_{h} (n_{2}._{h} A),\) so we get \[B\boxplus_{h} C=\left\{\left. x, \left(\dfrac{\mu^q_B(x)+\mu^q_C(x)-2\mu^q_B(x)\mu^q_C(x)}{1-\mu^q_B(x)\mu^q_C(x)}\right)^{1/q}, \left(\dfrac{\nu^q_B(x)\nu^q_C(x)}{\nu^q_B(x)+\nu^q_C(x)-\nu^q_B(x)\nu^q_C(x)}\right)^{1/q} \right| x\in X \right\}.\] Further, we can get \begin{align*} &\left(\dfrac{\mu^q_B(x)+\mu^q_C(x)-2\mu^q_B(x)\mu^q_C(x)}{1-\mu^q_B(x)\mu^q_C(x)}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{\dfrac{n_{1}\mu^q_A(x)}{1+(n_{1}-1)\mu^q_A(x)}+\dfrac{n_{2}\mu^q_A(x)}{1+(n_{2}-1)\mu^q_A(x)}-2\dfrac{n_{1}\mu^q_A(x)}{1+(n_{1}-1)\mu^q_A(x)}\dfrac{n_{2}\mu^q_A(x)}{1+(n_{2}-1)\mu^q_A(x)}}{1-\dfrac{n_{1}\mu^q_A(x)}{1+(n_{1}-1)\mu^q_A(x)}\dfrac{n_{2}\mu^q_A(x)}{1+(n_{2}-1)\mu^q_A(x)}}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{n_{1}\mu^q_A(x)(1+n_{2}\mu^q_A(x)-\mu^q_A(x))+n_{2}\mu^q_A(x)(1+n_{1}\mu^q_A(x)-\mu^q_A(x))-2n_{1}\mu^q_A(x)n_{2}\mu^q_A(x)}{(1+n_{1}\mu^q_A(x)-\mu^q_A(x))(1+n_{2}\mu^q_A(x)-\mu^q_A(x))-n_{1}\mu^q_A(x)n_{2}\mu^q_A(x)}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{(n_{1}+n_{2})\mu^q_A(x)-(n_{1}+n_{2})\mu^q_A(x)}{1+(n_{1}+n_{2}-2)\mu^q_A(x)-(n_{1}+n_{2}-1)\mu^q_A(x)}\right)^{1/q}\end{align*} \begin{align*} &=\left(\dfrac{(n_{1}+n_{2})\mu^q_A(x)(1-\mu^q_A(x))}{(1+(n_{1}+n_{2}-1)\mu^q_A(x))(1-\mu^q_A(x))}\right)^{1/q}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\\ n_{1}._{h} A&=\left(\dfrac{(n_{1}+n_{2})\mu^q_A(x)}{1+(n_{1}+n_{2}-1)\mu^q_A(x)}\right)^{1/q},\end{align*} and \begin{align*} &\left(\dfrac{\nu^q_B(x)\nu^q_C(x)}{\nu^q_B(x)+\nu^q_C(x)-\nu^q_B(x)\nu^q_C(x)}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{\dfrac{\nu^q_A(x)}{n_{1}-(n_{1}-1)\nu^q_A(x)} \dfrac{\nu^q_A(x)}{n_{2}-(n_{2}-1)\nu^q_A(x)}}{\dfrac{\nu^q_A(x)}{n_{1}-(n_{1}-1)\nu^q_A(x)}+ \dfrac{\nu^q_A(x)}{n_{2}-(n_{2}-1)\nu^q_A(x)}-\dfrac{\nu^q_A(x)}{n_{1}-(n_{1}-1)\nu^q_A(x)} \dfrac{\nu^q_A(x)}{n_{2}-(n_{2}-1)\nu^q_A(x)}}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{\nu^q_A(x)\nu^q_A(x)}{\nu^q_A(x)(n_{2}+\nu^q_A(x)-n_{2}\nu^q_A(x))+\nu^q_A(x)(n_{1}+\nu^q_A(x)-n_{1}\nu^q_A(x))-\nu^q_A(x)\nu^q_A(x)}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{\nu^q_A(x)}{(n_{2}+\nu^q_A(x)-n_{2}\nu^q_A(x))+(n_{1}+\nu^q_A(x)-n_{1}\nu^q_A(x))-\nu^q_A(x)}\right)^{1/q}\\ &\;\;\; n_{2}._{h} A=\left(\dfrac{\nu^q_A(x)}{(n_{1}+n_{2})-(n_{1}+n_{2}-1)\nu^q_A(x)}\right)^{1/q}.\end{align*} Since \[(n_{1}+n_{2})._{h} A =\left\{\left.\left( x, \left(\dfrac{(n_{1}+n_{2})\mu^q_A(x)}{1+(n_{1}+n_{2}-1)\mu^q_A(x)}\right)^{1/q} ,\left(\dfrac{\nu^q_A(x)}{(n_{1}+n_{2})-(n_{1}+n_{2}-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm}\right) \right.| x\in X \right\},\] so we finally get \((n_{1}._{h} A)\boxplus_{h} (n_{2}._{h} A)=(n_{1}+n_{2})._{h} A\).(ii) By Equations (1) and (2), we have
\[n._{h} A= \left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}=\left( \mu_B(x),\nu_B(x)\right),\] and \[n._{h} B= \left\{\left.\left( x, \left(\dfrac{n\mu^q_B(x)}{1+(n-1)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_B(x)}{n-(n-1)\nu^q_B(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\} \left( \mu_C(x),\nu_C(x)\right).\] Since \(B\boxplus_{h} C=(n._{h} A)\boxplus_{h}(n._{h} B)\), so we get \[B\boxplus_{h} C=\left\{\left.\left( x, \left(\dfrac{\mu^q_B(x)+\mu^q_C(x)-2\mu^q_B(x)\mu^q_C(x)}{1-\mu^q_B(x)\mu^q_C(x)}\right)^{1/q},\left(\dfrac{\nu^q_B(x)\nu^q_C(x)}{\nu^q_B(x)+\nu^q_C(x)-\nu^q_B(x)\nu^q_C(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}.\] Further, we can get \begin{align*} &\left(\dfrac{\mu^q_B(x)+\mu^q_C(x)-2\mu^q_B(x)\mu^q_C(x)}{1-\mu^q_B(x)\mu^q_C(x)}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}+\dfrac{n\mu^q_B(x)}{1+(n-1)\mu^q_B(x)}-2\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)} \dfrac{n\mu^q_B(x)}{1+(n-1)\mu^q_B(x)}}{1-\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)} \dfrac{n\mu^q_B(x)}{1+(n-1)\mu^q_B(x)}}\right)^{1/q}\end{align*} \begin{align*} &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{n\mu^q_A(x)(1+n\mu^q_B(x)-\mu^q_B(x))+n\mu^q_B(x)(1+n\mu^q_A(x)-\mu^q_A(x))-2n\mu^q_A(x)n\mu^q_B(x)}{(1+n\mu^q_B(x)-\mu^q_B(x)) (1+n\mu^q_A(x)-\mu^q_A(x))-n\mu^q_A(x)n\mu^q_B(x)}\right)^{1/q}\\ &\;\;\;(n._{h} A)=\left(\dfrac{n\mu^q_A(x)+n\mu^q_B(x)-2n\mu^q_A(x)\mu^q_B(x)}{1+(n-1)(\mu^q_A(x)+\mu^q_B(x))-(2n-1)\mu^q_A(x)\mu^q_B(x)}\right)^{1/q},\end{align*} and \begin{align*} &\left(\dfrac{\nu^q_B(x)\nu^q_C(x)}{\nu^q_B(x)+\nu^q_C(x)-\nu^q_B(x)\nu^q_C(x)}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)} \dfrac{\nu^q_B(x)}{n-(n-1)\nu^q_B(x)}}{\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}+\dfrac{\nu^q_B(x)}{n-(n-1)\nu^q_B(x)}-\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)} \dfrac{\nu^q_B(x)}{n-(n-1)\nu^q_B(x)}}\right)^{1/q}\\ &\;\;\;\;\;\;\;\;\;\;\;\;=\left(\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)(n+\nu^q_B(x)-n\nu^q_B(x))+\nu^q_B(x)(n+\nu^q_A(x)-n\nu^q_A(x))-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\\ &\;\;\;(n._{h} B)=\left(\dfrac{\nu^q_A(x) \nu^q_B(x)}{n(\nu^q_A(x)+\nu^q_B(x))-(2n-1)\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}.\end{align*} Thus, \begin{align*} n._{h}&(A\boxplus_{h} B)\\ &=\left[ \left(\dfrac{n \dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}}{1+(n-1)\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}}\right)^{1/q}, \left(\dfrac{\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}}{n-(n-1)\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}}\right)^{1/q}\right],\\ &=\left[ \left(\dfrac{n\mu^q_A(x)+n\mu^q_B(x)-2n\mu^q_A(x)\mu^q_B(x)}{1+(n-1)(\mu^q_A(x)+\mu^q_B(x))-(2n-1)\mu^q_A(x)\mu^q_B(x)}\right)^{1/q},\left(\dfrac{\nu^q_A(x) \nu^q_B(x)}{n(\nu^q_A(x)+\nu^q_B(x))-(2n-1)\nu^q_A(x)\nu^q_B(x)}\right)^{1/q} \right]. \end{align*} Comparing above results, we finally get \((n._{h} A)\boxplus_{h} (n._{h} B)=n._{h}(A\boxplus_{h} B)\).(v) By Equations (1) and (2), we have
\[n_{1}._{h} A=\left\{\left.\left( x, \left(\dfrac{n_{1}\mu^q_A(x)}{1+(n_{1}-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{\nu^q_A(x)}{n_{1}-(n_{1}-1)\nu^q_A(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}=\left( \mu_B(x),\nu_B(x)\right),\] and \[n_{2}._{h}(n_{1}._{h} A)=\left\{\left.\left( x, \left(\dfrac{n_{2}\mu_B(x)}{1+(n_{2}-1)\mu_B(x)}\right)^{1/q},\left(\dfrac{\nu_B(x)}{n_{2}-(n_{2}-1)\nu_B(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}.\] Further we can get \[\left(\dfrac{n_{2}\mu_B(x)}{1+(n_{2}-1)\mu_B(x)}\right)^{1/q}=\left(\dfrac{n_{2} \dfrac{n_{1}\mu^q_A(x)}{1+(n_{1}-1)\mu^q_A(x)}}{1+(n_{2}-1) \dfrac{n_{1}\mu^q_A(x)}{1+(n_{1}-1)\mu^q_A(x)}}\right)^{1/q} =\left(\dfrac{n_{1}n_{2}\mu^q_A(x)}{1+(n_{1}n_{2}-1)\mu^q_A(x)}\right)^{1/q},\] and \[\left(\dfrac{\nu_B(x)}{n_{2}-(n_{2}-1)\nu_B(x)}\right)^{1/q} =\left(\dfrac{\dfrac{\nu^q_A(x)}{n_{1}-(n_{1}-1)\nu^q_A(x)}}{n_{2}-(n_{2}-1) \dfrac{\nu^q_A(x)}{n_{1}-(n_{1}-1)\nu^q_A(x)}}\right)^{1/q}=\left(\dfrac{\nu^q_A(x)}{n_{1}n_{2}-(n_{1}n_{2}-1)\nu^q_A(x)}\right)^{1/q}.\] Since \[n_{1}(n_{2}._{h}) A=\left\{\left.\left( x, \left(\dfrac{n_{1}n_{2}\mu^q_A(x)}{1+(n_{1}n_{2}-1)\mu^q_A(x)}\right)^{1/q} ,\left(\dfrac{\nu^q_A(x)}{n_{1}n_{2}-(n_{1}n_{2}-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\},\] so we finally get \(n_{2}._{h}(n_{1}._{h} A)=(n_{1}n_{2})._{h} A\).Theorem 13. If \( A, B \in q-ROFS(X)\), then for any positive integer \(n\), we have
- (i) \(n._{h}(A\cap B)=({n._{h}}A) \cap ({n._{h}}B),\)
- (ii) \(n._{h}(A\cup B)=({n._{h}}A) \cup ({n._{h}}B),\)
- (iii) \({(A\cap B)^{\wedge_{h}}}^n={A^{\wedge_{h}}}^n \cap {B^{\wedge_{h}}}^n,\)
- (iv) \({(A\cup B)^{\wedge_{h}}}^n={A^{\wedge_{h}}}^n \cup {B^{\wedge_{h}}}^n.\)
Proof. We shall prove (ii), (iv) and (i), (iii) can be proved analogously.
- (i) Since
\begin{align*}(A\cap B)&=\left\{\left( x, \min\left\{\mu_A(x),\mu_B(x)\right\},\max\left\{\nu_A(x),\nu_B(x)\right\} \right) | x\in X \right\},\\
n._{h}(A\cap B)&=\left\{\left( x, \mu_C(x),\nu_C(x) \right) | x\in X \right\},\\
n._{h}A&=\left\{\left( x, \mu_D(x),\nu_D(x) \right) | x\in X \right\},\end{align*}
and\begin{align*} n._{h}B=\left\{\left( x, \mu_E(x),\nu_E(x) \right) | x\in X \right\},\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\end{align*}
where
\[\mu_C(x)=\left(\dfrac{n\left(\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\right)}{1+(n-1)\left(\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\right)}\right)^{1/q},\]
and
\[\nu_C(x)=\left(\dfrac{\left(\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\right)}{n-(n-1)\left(\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\right)}\right)^{1/q}.\]
So, we have
and\begin{align} \label{eq3} \mu_C(x)&=\left(\dfrac{n\left(\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\right)}{1+(n-1)\left(\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\right)}\right)^{1/q}\notag\\ &=\min\left\{\left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{n\mu^q_B(x)}{1+(n-1)\mu^q_B(x)}\right)^{1/q}\hspace{0.2cm}\right\}\notag\\ &=\min\left\{\mu_D(x),\mu_E(x) \right\}, \end{align}(3)Comparing Equations (3) and (4), we get \begin{align*}({n._{h}}A) \cap ({n._{h}}B)&=\left\{\left( x, \min\left\{\mu_D(x),\nu_D(x)\right\},\max\left\{\mu_E(x),\nu_E(x)\right\} \right) | x\in X \right\}\\ &=\left[\min\left\{\left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q} \hspace{0.2cm}\right\},\right. \\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left. \max\left\{\left(\dfrac{n\mu^q_B(x)}{1+(n-1)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_B(x)}{n-(n-1)\nu^q_B(x)}\right)^{1/q} \right\}\right].\end{align*} Thus, we have \(n._{h}(A\cap B)=(n._{h} A) \cap (n._{h} B)\).\begin{align} \nu_C(x)&=\left(\dfrac{\left(\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\right)}{n-(n-1)\left(\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\right)}\right)^{1/q}\notag\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\end{align} \begin{align} \label{eq4}&=\max\left\{\left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q},\left(\dfrac{\nu^q_B(x)}{n-(n-1)\nu^q_B(x)}\right)^{1/q}\right\}\notag\\ &=\max\left\{\nu_D(x),\nu_E(x) \right\}.\end{align}(4)
- (iii) Since
\[(A\cap B)=\left\{\left( x, \min\left\{\mu_A(x),\mu_B(x)\right\},\max\left\{\nu_A(x),\nu_B(x)\right\} \right) | x\in X \right\},\]
so
\begin{align*}
{(A\cap B)^{\wedge_{h}}}^n&=\left\{\left( x, \mu_C(x),\nu_C(x) \right) | x\in X \right\},\\
{A^{\wedge_{h}}}^n&=\left\{\left( x, \mu_D(x),\nu_D(x) \right) | x\in X \right\},\end{align*}
and
\begin{align*}
{B^{\wedge_{h}}}^n&=\left\{\left( x, \mu_E(x),\nu_E(x) \right) | x\in X \right\},\end{align*}
where
\[\mu_C(x)=\left(\dfrac{\left(\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\right)}{n-(n-1)\left(\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\right)}\right)^{1/q},\]
and
\[\nu_C(x)=\left(\dfrac{n\left(\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\right)}{1+(n-1)\left(\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\right)}\right)^{1/q}.\]
So, we have
and\begin{align} \label{eq5} \mu_C(x)&=\left(\dfrac{\left(\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\right)}{n-(n-1)\left(\min\left\{\mu^q_A(x),\mu^q_B(x)\right\}\right)}\right)^{1/q}\notag\\ &=\min\left\{\left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{\mu^q_B(x)}{n-(n-1)\mu^q_B(x)}\right)^{1/q}\hspace{0.2cm}\right\}\notag\\ &=\min\left\{\mu_D(x),\mu_E(x) \right\},\end{align}(5)Comparing Equations (5) and (6), we get \begin{align*} {A^{\wedge_{h}}}^n \cap {B^{\wedge_{h}}}^n&=\left\{\left( x, \min\left\{\mu_D(x),\nu_D(x)\right\},\max\left\{\mu_E(x),\nu_E(x)\right\} \right) | x\in X \right\}\\ &=\left[\min\left\{\left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \right\}\right.,\\ &\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left.\max\left\{\left(\dfrac{\mu^q_B(x)}{n-(n-1)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{n\nu^q_B(x)}{1+(n-1)\nu^q_B(x)}\right)^{1/q} \hspace{0.2cm}\right\} \right].\end{align*} Hence, \({(A\cap B)^{\wedge_{h}}}^n={A^{\wedge_{h}}}^n \cap {B^{\wedge_{h}}}^n\).\begin{align} \label{eq6} \nu_C(x)&=\left(\dfrac{n\left(\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\right)}{1+(n-1)\left(\max\left\{\nu^q_A(x),\nu^q_B(x)\right\}\right)}\right)^{1/q}\notag\\ &=\max\left\{\left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q},\left(\dfrac{n\nu^q_B(x)}{1+(n-1)\nu^q_B(x)}\right)^{1/q}\hspace{0.2cm}\right\}\notag\\ &=\max\left\{\nu_D(x),\nu_E(x)\right\}.\end{align}(6)
6. Necessity and possibility operators on q-rung orthopair fuzzy sets
In this section, we defined the necessity and possibility operators on q-rung orthopair fuzzy sets and investigated several properties of Hamacher operations.Definition 3. For any q-rung orthopair fuzzy set \(A\), the necessity \((\Box)\) and the possibility \((\Diamond)\) operators are defined as follows; \begin{align*}\Box A&=\left\{\left.\left( x, \mu_A(x),\left(1-\mu^q_A(x)\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\},\\ \Diamond A&=\left\{\left.\left( x, \left(1-\nu^q_A(x)\right)^{1/q},\nu_A(x)\hspace{0.2cm}\right) \right| x\in X \right\}.\end{align*}
Theorem 14. If \(A, B\in q-ROFS(X)\), then
- (i) \(\Box(A\boxplus_{h} B)=\Box A\boxplus_{h} \Box B,\)
- (ii) \(\Diamond (A\boxplus_{h} B)=\Diamond A\boxplus_{h} \Diamond B\).
Proof. (i) \begin{align*}\Box\left(A\right.&\left.\boxplus_{h} B\right)\\&= \left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}, \left(1-\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{(1-\mu^q_A(x))(1-\mu^q_B(x))}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}\\ &=\Box A\boxplus_{h} \Box B.\end{align*} (ii) \begin{align*} \Diamond (A\boxplus_{h} B)&= \left\{\left.\left( x, \left(1-\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q},\left(\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\hspace{0.2cm}\right) \right| x\in X \right\}\\ &=\Diamond A\boxplus_{h} \Diamond B.\end{align*} Hence the theorem is proved.
Theorem 15. If \(A, B\in q-ROFS(X)\), then
- (i) \(\Box(A\boxtimes_{h} B)=\Box A\boxtimes_{h} \Box B,\)
- (ii) \(\Diamond(A\boxtimes_{h} B)=\Diamond A\boxtimes_{h} \Diamond B\).
Proof. (i) \begin{align*}\Box(A&\boxtimes_{h} B)\\ &= \left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}, \left(1-\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\Box A\boxtimes_{h} \Box B.\end{align*} (ii) \begin{align*}\Diamond(A&\boxtimes_{h} B)\\ &=\left\{\left.\left( x, \left(1-\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{(1-\nu^q_A(x))(1-\nu^q_B(x))}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\Diamond A\boxtimes_{h} \Diamond B.\end{align*} Hence the theorem is proved.
Theorem 16. If \(A, B\in q-ROFS(X)\), then
- (i) \(\left(\Box(A^C\boxplus_{h} B^C)\right)^{C}=\Diamond A\boxtimes_{h} \Diamond B,\)
- (ii) \(\left(\Box(A^C\boxtimes_{h} B^C)\right)^{C}=\Diamond A\boxplus_{h} \Diamond B\).
Proof. (i) \begin{align*}\Box(A&^C\boxplus_{h} B^C)\\ &= \left\{\left.\left( x, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}, \left(1-\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}, \left(\dfrac{(1-\nu^q_A(x))(1-\nu^q_B(x))}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\},\\ \left(\Box\left(A^C\right.\right.&\boxplus_{h}\left.\left. B^C\right)\right)^{C}\\ &=\left\{\left.\left( x, \left(\dfrac{(1-\nu^q_A(x))(1-\nu^q_B(x))}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q},\left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{1-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q} \right) \right| x\in X \right\}\\ &=\Diamond A\boxtimes_{h} \Diamond B.\end{align*} (ii) \begin{align*}\Box(A^C&\boxtimes_{h} B^C)\\ &= \left\{\left.\left( x, \left(\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}, \left(1-\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\},\end{align*} \begin{align*} \left(\Box\left(A^C\right.\right.&\left.\left.\boxtimes_{h} B^C\right)\right)^{C}\\ &= \left\{\left.\left( x, \left(\dfrac{\nu^q_A(x)+\nu^q_B(x)-2\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)\nu^q_B(x)}{\nu^q_A(x)+\nu^q_B(x)-\nu^q_A(x)\nu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\Diamond A\boxplus_{h} \Diamond B.\end{align*} Hence the theorem is proved.
Theorem 17. If \(A, B\in q-ROFS(X)\), then
- (i) \(\left(\Diamond(A^C\boxplus_{h} B^C)\right)^{C}=\Box A\boxtimes_{h} \Box B,\)
- (ii) \(\left(\Diamond(A^C\boxtimes_{h} B^C)\right)^{C}=\Box A\boxplus_{h} \Box B\).
Proof. (i) \begin{align*} \Diamond(A^C&\boxplus_{h} B^C)\\ &=\left\{\left.\left( x, \left(1-\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q},\left(\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q},\left(\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &= \left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q},\left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{\mu^q_A(x)+\mu^q_B(x)-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\Box A\boxtimes_{h} \Box B. \end{align*} (ii) \begin{align*} \Diamond\left(A^C\right.&\left.\boxtimes_{h} B^C\right)\\ &= \left\{\left.\left( x, \left(1-\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{(1-\mu^q_A(x))(1-\mu^q_B(x))}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q},\left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q} \right) \right| x\in X \right\},\end{align*}\begin{align*} \Diamond(A^C\boxtimes_{h} B^C)^{C} &= \left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)+\mu^q_B(x)-2\mu^q_A(x)\mu^q_B(x)}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}, \left(\dfrac{(1-\mu^q_A(x))(1-\mu^q_B(x))}{1-\mu^q_A(x)\mu^q_B(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\Box A\boxplus_{h} \Box B.\end{align*} Hence the theorem is proved.
Theorem 18. If \(A\in q-ROFS(X)\), then for any positive integer \(n\), we have
- (i) \(\Box(n._{h}A)=n._{h}(\Box A)\),
- (ii) \(\Diamond(n._{h}A)=n._{h}(\Diamond A)\),
- (iii) \(\Box {A^{\wedge_{h}}}^n={(\Box A)^{\wedge_{h}}}^n\),
- (iv) \(\Diamond {A^{\wedge_{h}}}^n={(\Diamond A)^{\wedge_{h}}}^n\).
Proof. (i) \begin{align*} \Box(n._{h}A)&=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q},\left(1-\left(\left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\hspace{0.2cm}\right)^q\right)^{1/q}\right) \right| x\in X \right\}\end{align*} \begin{align*} &=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}, \left(1-\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{1+(n-1)\mu^q_A(x)-n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}, \left(\dfrac{1+n\mu^q_A(x)-\mu^q_A(x)-n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{1-\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\},\\ n._{h}(\Box A)&=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{\left(\left(1-\mu^q_A(x)\right)^{1/q}\right)^q}{n-(n-1)\left(\left(1-\mu^q_A(x)\right)^{1/q}\right)^q}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{1-\mu^q_A(x)}{n-(n-1)\left(1-\mu^q_A(x)\right)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{1-\mu^q_A(x)}{1+(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}.\end{align*} Hence, \(\Box(n._{h}A)=n._{h}(\Box A)\).
(ii)
\begin{align*} \Diamond(n._{h}A)&=\left\{\left.\left( x, \left(1-\left(\left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right)^q\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(1-\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n-(n-1)\nu^q_A(x)-\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n-n\nu^q_A(x)+\nu^q_A(x)-\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n(1-\nu^q_A(x))}{n-(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\},\\ n._{h}(\Diamond A)&=\left\{\left.\left( x, \left(\dfrac{n(\left(1-\nu^q_A(x)\right)^{1/q})^q}{1+(n-1)(\left(1-\nu^q_A(x)\right)^{1/q})^q}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n(1-\nu^q_A(x))}{1+(n-1)(1-\nu^q_A(x))}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{n(1-\nu^q_A(x))}{n-(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{\nu^q_A(x)}{n-(n-1)\nu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}.\end{align*} Hence, \(\Diamond(n._{h}A)=n._{h}(\Diamond A)\).(iii)
\begin{align*} \Box {A^{\wedge_{h}}}^n&=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(1-\left(\left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}\right)^q\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(1-\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{n-(n-1)\mu^q_A(x)-\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{n-n\mu^q_A(x)+\mu^q_A(x)-\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{n(1-\mu^q_A(x))}{n-(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\},\\ {(\Box A)^{\wedge_{h}}}^n&=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{n(\left(1-\mu^q_A(x)\right)^{1/q})^q}{n-(n-1)(\left(1-\mu^q_A(x)\right)^{1/q})^q}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{n(1-\mu^q_A(x))}{n-(n-1)(1-\mu^q_A(x))}\right)^{1/q}\right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\mu^q_A(x)}{n-(n-1)\mu^q_A(x)}\right)^{1/q},\left(\dfrac{n(1-\mu^q_A(x))}{n-(n-1)\mu^q_A(x)}\right)^{1/q}\right) \right| x\in X \right\}.\end{align*} Hence, \(\Box {A^{\wedge_{h}}}^n={(\Box A)^{\wedge_{h}}}^n\).(iv)
\begin{align*} \Diamond {A^{\wedge_{h}}}^n&=\left\{\left.\left( x, \left(1-\left(\left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q}\right)^q\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(1-\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{1+(n-1)\nu^q_A(x)-n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{1-\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \right) \right| x\in X \right\},\\ {(\Diamond A)^{\wedge_{h}}}^n&=\left\{\left.\left( x, \left(\dfrac{\left(\left(1-\nu^q_A(x)\right)^{1/q}\right)^q}{1+(n-1)\left(\left(1-\nu^q_A(x)\right)^{1/q}\right)^q}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \right) \right| x\in X \right\}\\ &=\left\{\left.\left( x, \left(\dfrac{\left(1-\nu^q_A(x)\right)}{1+(n-1)\left(1-\nu^q_A(x)\right)}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \right) \right| x\in X \right\}\\ &=\left\{\left( x, \left(\dfrac{1-\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q}, \left(\dfrac{n\nu^q_A(x)}{1+(n-1)\nu^q_A(x)}\right)^{1/q} \hspace{0.2cm} \right) | x\in X \right\}.\end{align*} Hence, \(\Diamond {A^{\wedge_{h}}}^n={(\Diamond A)^{\wedge_{h}}}^n\).7. Comparison analysis of the proposed model with IF and PF models
An IFSs and PFSs are particular cases of q-ROFSs. The flexibility and the effectiveness of a q-ROF model can be proven as follows. Suppose that \((\mu_A(x),\nu_A(x))\) is an IF grade, where \(\mu_A(x)\in[0,1],\nu_A(x)\in[0,1]\) and \(\mu_A(x)+\nu_A(x)\leq 1\), since \(\mu^q_A(x)\leq \mu_A(x), \nu^q_A(x)\leq \nu_A(x) ~q\geq 1\), so we have \(\mu^q_A(x)+\nu^q_A(x)\leq 1\). Thus, every IF grade is also a PF grade, as well as a q-ROF grade. However, there are q-ROF grades that are not IF nor PF grades. For example, \((0.9,0.8)\) , here \((0.9)^5+(0.8)^5=1\) , but \(0.9+0.8=1.7>1\) and \((0.9)^2+(0.8)^2=1.45>1\). This implies that the class of q-ROFSs extends the classes of IFSs and PFSs.8. Conclusion
A q-ROFS model is an extension of the IF and PF models. However, the IFSs and PFSs are all good ways to deal with fuzzy information, but q-ROFSs are more general as compared to these classical models, because when \(q=1\), the model reduces to the IF model, and when \(q=2\), it reduces to the PF model. In this research article, we have applied the more generalized and powerful concept of q-ROFSs to the most productive theory of Hamacher operations. The work has extended the Hamacher operation results under q-rung orthopair fuzzy environment. In this paper, we have developed the Hamacher operations on q-rung orthopair fuzzy sets and investigated their algebraic properties. We also proved that the set of all q-ROFSs with respect to Hamacher sum and Hamacher product forms a commutative monoid. A study of the algebraic structure of q-ROFSs with respect to Hamacher operations gives us a deep insight into the applications. Further, we constructed Hamacher scalar multiplication \(({n._{h}}A)\) and Hamacher exponentiation \((A^{\wedge_{h}n})\) operations on q-rung orthopair fuzzy set \(A\) and investigated their algebraic properties. Finally, we defined the necessity and possibility operators based on Hamacher q-rung orthopair fuzzy sets and several properties are verified.9. Future scope
Thus there remains scope for studying more properties of these sets arising from those other defining set operations that may be thought of using other ways of combining the functions \(\mu; \nu\). In further research, we may apply these operators in the field of different areas, for example, dynamic decision and consensus , business and marketing management, design, engineering and manufacturing, information technology and networking applications, human resources management, military applications, energy management, geographic information system applications etc.Conflicts of Interest
The author declares no conflict of interest.References
- Zadeh, L. A. (1965). Fuzzy sets. Information Control, 8 (3), 338-356. [Google Scholor]
- Atanassov, K. T. (1986). Intuitionistic fuzzy sets. Fuzzy Sets and Systems, 20(1), 87-96, 1986. [Google Scholor]
- Liu, X., Kim, H., Feng, F., & Alcantud, J. (2018). Centroid transformations of intuitionistic fuzzy values based on aggregation operators. Mathematics, 6, 215.[Google Scholor]
- Yager, R. R. (2013). Pythagorean fuzzy subsets.In: 2013 Proc Joint IFSA World Congress and NAFIPS Annual Meeting, Edmonton, Canada, 24-28, 57-61. [Google Scholor]
- Yager, R. R., & Abbasov, A. M. (2014). Pythagorean membership grades, complex numbers, and decision making. International Journal of Intelligent Systems, 28(5), 436-452.[Google Scholor]
- Zhang, X. L., & Xu, Z. S. (2014). Extension of TOPSIS to multiple criteria decision making with pythagorean fuzzy sets. International Journal of Intelligent Systems, 29(12), 1061-1078. [Google Scholor]
- Zeng,S., Chen,J., & Li,X. (2016). A hybrid method for pythagorean fuzzy multiple-criteria decision making. International Journal of Information Technology & Decision Making, 15(02), 403-422. [Google Scholor]
- Garg, H. (2016). A new generalized pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. International Journal of Intelligent Systems, 31(9), 886-920. [Google Scholor]
- Hamachar, H. (1978). Uber logische verknunpfungenn unssharfer Aussagen und deren Zugenhorige Bewertungsfunktione Trappl, Klir, Riccardi (Eds.). Progress in Cybernatics and Systems Research, 3, 276-288. [Google Scholor]
- Gao, H. (2018). Pythagorean fuzzy Hamacher prioritized aggregation operators in multiple attribute decision making. Journal of Intelligent and Fuzzy Systems, 35(2), 2229-2245. [Google Scholor]
- Wei, G. W., Lu, M., Tang, X., & Wei, Y. (2018). Pythagorean Hesitant fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. International Journal of Intelligent Systems, 33(6), 1197-1233. [Google Scholor]
- Wu, S. J., Wei, G. W. (2017). Pythagorean fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. International Journal of Knowledge-based and Intelligent Engineering Systems, 21(3), 189-201. [Google Scholor]
- Zhou, L. Y., GW., & Zhao, X. F. (2014). Hesitant fuzzy Hamacher aggregation operators and their application to multiple attribute decision making. International Journal of Intelligent Systems, 26(6), 2689-2699. [Google Scholor]
- Silambarasan, I., & Sriram, S. (2019). International Journal of Scientific & Technology Research, 8 (8), 1505-1509. [Google Scholor]
- Yager, R. R. (2017). Generalized orthopair fuzzy sets. IEEE Transactions on Fuzzy Systems, 25(5), 1222-1230. [Google Scholor]
- Liu, P., & Wang, P. (2018). Some q-rung orthopair fuzzy aggregation operators and their applications to multiple-attribute decision making. International Journal of Intelligent Systems, 33(2), 259-280. [Google Scholor]
- Wei, G., Gao, H., & Wei, Y. (2018). Some q-rung orthopair fuzzy Heronian mean operators in multiple attribute decision-making. International Journal of Intelligent Systems, 33, 1426-1458. [Google Scholor]
- Deschrijver, G., Cornelis, C., & Kerre, E. E. (2004). On the representation of intuitionistic fuzzy t-norms and t-conorms. IEEE Transactions on Fuzzy Systems, 12(1), 45-61. [Google Scholor]
- Roychowdhury, S., Wang, B. H. (1998). On generalized Hamacher families of triangular operators. International Journal of Approximate Reasoning, 19(3-4), 419-439. [Google Scholor]
- Deschrijver, G., Kerre, E. E. (2002). A generalization of operators on intuitionistic fuzzy sets using triangular norms and conorms. Notes Intuitionistic Fuzzy Sets, 8(1), 19-27. [Google Scholor]