Open Journal of Mathematical Sciences
Vol. 6 (2022), Issue 1, pp. 192 – 204
ISSN: 2523-0212 (Online) 2616-4906 (Print)
DOI: 10.30538/oms2022.0188
Long-time solutions for some mixed boundary value problems depicting motions of a class of Maxwell fluids with pressure dependent viscosity
Constantin Fetecau\(^{1,*}\), Dumitru Vieru\(^{2}\), Waqas Nazeer\(^{3}\) and Shehraz Akhtar\(^{4}\)
\(^1\) Section of Mathematics, Academy of Romanian Scientists, Bucharest 050094, Romania.
\(^{2}\) Department of Theoretical Mechanics, Technical University of Iasi, Iasi 700050, Romania.
\(^{3}\) Department of Mathematics, Government College University, Lahore 54000, Pakistan.
\(^{4}\) Department of Mathematics, The Islamia University of Bahawalpur, Rahim Yar Khan Campus, Pakistan.
Correspondence should be addressed to Constantin Fetecau at c_fetecau@yahoo.com
Abstract
Keywords:
1. Introduction
The study of the motion of a fluid between parallel walls is both of theoretical and practical interest. It was extensively developed due to the various applications in engineering problems. However, very few studies from the existing literature took into consideration the fact that the fluid viscosity does not remain constant at high values of the pressure. The first who remarked this variation of viscosity with the pressure was Stokes in 1845 [1]. During the time experimental investigations (see for instance the book of Bridgman [2] for the pertinent literature prior to 1931, Cutler et al., [3], Johnson and Tewaarwerk [4], Bair and Winer [5] or more recently Bair and Kottke [6] and Prusa et al., [7] have certified this supposition. In elastohydrodynamic lubrication, for instance, the effect of the pressure on viscosity cannot be neglected. In addition, relatively recent Kannan and Rajagopal [8] have remarked that in many motions with practical applications the gravity has a significant influence. Its effects are stronger if the pressure varies along the direction in which the gravity acts.
The first exact steady solutions for isothermal unsteady motions of the incompressible Newtonian fluids (INF) with pressure-dependent viscosity in which the effects of gravity are taken into consideration have been established by Rajagopal [9,10] and Prusa [11]. Analytical expressions of the long-time (permanent or Long) solutions corresponding to the modified Stokes' problems for such fluids with power-law dependence of viscosity on the pressure have been recently determined by Fetecau and Agop [12] and Fetecau and Vieru [13]. Some of them have been already extended to incompressible Maxwell fluids (IMF) of the same type by Fetecau and Rauf [14] and Fetecau et al., [15].
However, all the above mentioned results correspond to boundary value problems in which the velocity is given on the boundary. In practice, there are many situations in which the shear stress is given on a part of the boundary. They lead to mixed boundary value problems. Long-time solutions for such problems describing motions of IFM with power-law dependence of viscosity on the pressure have been determined by Fetecau et al., [16,17]. The purpose of this note is to provide closed-form expressions for the dimensionless velocity, shear stress and normal stress fields corresponding to such motions of a new class of IMF with power-law dependence of viscosity on the pressure. The obtained results have been easy particularized to recover similar solutions for the classical Incompressible Maxwell fluids (CIMF) performing the same motions. The influence of the pressure-viscosity coefficient on the fluid motion were graphically underlined and discussed.
2. Constitutive and governing equations
The constitutive equations of IMF with pressure-dependent viscosity are given by the following relations (see Karra et al., [18]Let us now consider an IMF with power-law dependence of viscosity on the pressure of the form (3) at rest between two infinite horizontal parallel plates at the distance d one of the other. At the moment \(t = 0^{+}\) the lower plate begins to apply a time dependent shear stress
Due to the shear the fluid begins to move and, as well as Karra et al., [18], we are looking for a velocity field and pressure of the form
To do that we introduce the next non-dimensional variables, functions and parameters,
3. Long-time solutions
For distinction, we denote by \(u_{c}(y,t)\), \(\tau_{c}(y,t)\), \(\sigma_{c}(y,t)\) and \(u_{s}(y,t)\), \(\tau_{s}(y,t)\), \(\sigma_{s}(y,t)\) the dimensionless starting solutions corresponding to the two motions of IMF with power-law dependence of viscosity on the pressure induced by the lower plate that applies shear stresses of the form (4), respectively (5) to the fluid. These solutions can be presented as sums of the long-time components \(u_{\text{cp}}(y,t)\), \(\tau_{\text{cp}}(y,t)\), respectively \(u_{\text{sp}}(y,t)\), \(\tau_{\text{sp}}(y,t)\), \(\sigma_{\text{sp}}(y,t)\) and the corresponding transient components. Some time after the motion initiation, the fluid moves according to the starting solutions. After this time, when the transients disappear, the fluid motion is characterized by the long-time solutions which are independent of the initial conditions but satisfy the boundary conditions and the governing equations. In practice, this time is important for the experimental researchers who want to know the required time to touch the steady or permanent state. To determine this time the long-time solutions have to be known and we shall determine them in the following.3.1. Exact expressions for the long-time velocity fields \(u_{\text{cp}}(y,t)\) and \(u_{\text{sp}}(y,t)\)
In order to determine both components in a simple way and in the same time, let us denote by the dimensionless complex velocity defined by the relation,3.2. Exact expressions for the long-time shear stresses \(\tau_{\mathbf{\text{cp}}}(y,t)\) and \(\tau_{\mathbf{\text{sp}}}(y,t)\)
The dimensionless complex shear stress,3.3. Exact expressions for the normal stresses\(\sigma_{\mathbf{\text{cp}}}(y,t)\) and \(\sigma_{\mathbf{\text{sp}}}(y,t)\)
The complex normal stress \(\sigma_{p}(y,t)\) defined by the equality,4. Limiting cases
In this section, for a check of results that have been previously obtained, some limiting cases are considered and different known results from the existing literature are recovered.4.1. Case \(\omega \rightarrow 0\); Motion due to an exponential shear stress on the boundary
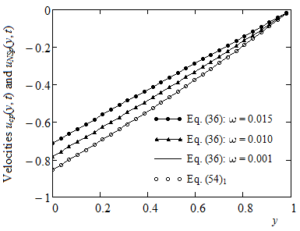
As we already justified in §2, the motions that have been previously studied are induced by the lower plate that applies a shear stress of the form (4) or (5) to the fluid. Making in Eq. (4), the corresponding motion is due to an exponential shear stress,Figure 1. Convergence of the long-time velocity \(u_{cp}(y,t)\) given by Eq. (36) to the corresponding Newtonian solution \(u_{NSp}(y)\) given by Eq. (54)\(_1\) for \(\alpha=0.8,Re{=}100,\mathrm{We}=1=t=5\) and \(\omega\rightarrow0\).
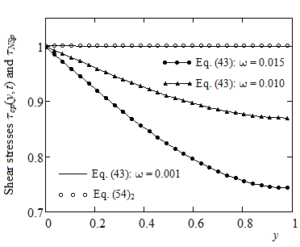
Figure 2. Convergence of the long-timee shear stress \(\tau_{\text{cp}}(y,t)\) given by Eq. (43) to the corresponding Newtonian solution \(\tau_{\text{NSp}}\) given by Eq. (54)\(_{2}\) for \(\alpha = 0.8,\text{Re} = 100,\text{We} = 1,t = 5\) and \(\omega \rightarrow 0\).
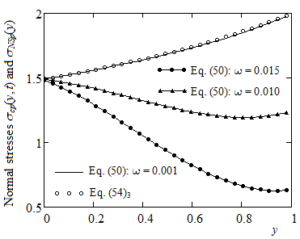
Figure 3. Convergence of long-time normal stress \(\sigma_{\text{cp}}(y,t)\) given by Eqs. (50) to the corresponding Newtonian solution \(\sigma_{\text{NSp}}(y)\) given by Eq. (54)\(_{3}\) for \(\alpha = 0.8,\text{Re} = 100,\text{We} = 1,t = 5\) and \(\omega \rightarrow 0\).
Consequently, the solutions \(u_{\text{Ep}}(y)\), \(\tau_{\text{Ep}}\) and \(\sigma_{\text{Ep}}(y)\) are given by the relations,
4.2. Case \(\alpha\rightarrow 0\) ; Long-time solutions for CIMF performing the initial motions
Based on some approximations of the standard Bessel functions \(J_{\nu}( \cdot )\)and \(Y_{\nu}( \cdot )\), namely4.3. Case \(\alpha\) and \(\omega\rightarrow 0\); Motion of CIMF due to an exponential shear stress on the boundary
Making \(\alpha \rightarrow 0\) in Eqs. (55) or \(\omega \rightarrow 0\) in (65), (67) and (69) one recovers the dimensionless steady solutions [17, Eqs. (84)-(86)],5. Some numerical results and conclusions
Generally, exact solutions corresponding to specific boundary value problems describe the behavior of a material subject to some deformations or motions. In addition, they can be used to verify various numerical schemes that are developed to study more complex problems. In the present work are established analytical expressions for the dimensionless long-time velocities and the adequate normal and shear stresses corresponding to isothermal motions of IMF with power-law dependence of viscosity on the pressure. The fluid motion, between two infinite horizontal parallel plates, is generated by the lower plate that applies time-dependent shear stresses to the fluid. Consequently, contrary to what is usually assumed in the existing literature, the shear stress is prescribed on a part of the boundary. Prescribing the shear stress on the plate is the same to give the force applied in order to move it.Obtained solutions are presented in simple forms in terms of standard Bessel functions. For a check of their corrections, the dimensionless steady solutions \(u_{\text{NSp}}(y)\),\(\tau_{\text{NSp}}\) and \(\sigma_{\text{NSp}}(y)\) corresponding to the isothermal motion induced by the lower plate that applies a constant shear stress S to an INF with power-law dependence of viscosity on the pressure have been used. More exactly, by means of Figures 1-3, the convergence of long-time solutions , and to these solutions has been graphically proved. In this way, as it was to be expected, we showed that the dimensionless steady solutions \(u_{\text{Ep}}(y)\), \(\tau_{\text{Ep}}\) and \(\sigma_{\text{Ep}}(y)\) corresponding to the isothermal motion generated by the lower plate that applies an exponential shear stress \(\lbrack 1 - \exp( - t/\lambda)\rbrack S\) to an IMF with power-law dependence of viscosity on the pressure are identical to \(u_{\text{NSp}}(y)\),\(\tau_{\text{NSp}}\), respectively \(\sigma_{\text{NSp}}(y)\).
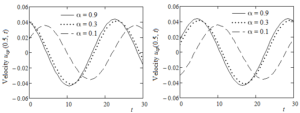
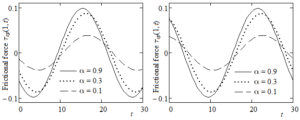
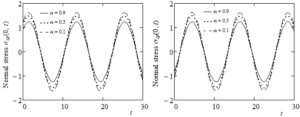
Finally, in order to emphasize some physical insight of results that have been here obtained, Figures 4-10 have been depicted for different values of the dimensionless pressure-viscosity coefficient and of the spatial variable y. The time variation of the mid plane velocities \(u_{\text{cp}}(0.5,t),u_{\text{sp}}(0.5,t)\), of frictional forces per unit area \(\tau_{\text{cp}}(1,t),\tau_{\text{sp}}(1,t)\) exerted by the fluid on the fixed plate and of the normal stresses \(\sigma_{\text{cp}}(0,t)\) and \(\sigma_{\text{sp}}(0,t)\) on the moving plate are presented in Figures 4-6 at increasing values of and fixed values of the other parameters. The oscillatory characteristic features of these entities of physical interest, as well as the phase difference between solutions corresponding to motions due to shear stresses of the form (4) or (5) on the boundary, are clearly visualized. From Figures 4 and 5 it also results that the larger pressure-viscosity coefficient the larger amplitude of velocity and shear stress oscillations. An opposite result appears in the case of normal stresses.
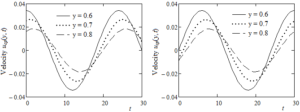
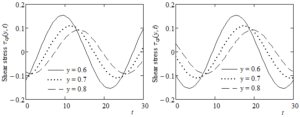
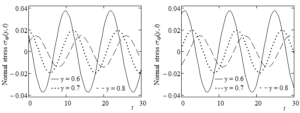
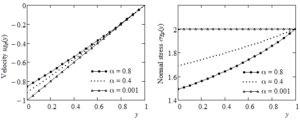
Figures 7-9 together present the time variations of \(u_{\text{cp}}(y,t)\) and \(u_{\text{sp}}(y,t)\),\(\tau_{\mathbf{\text{cp}}}\mathbf{(y,t)}\) and \(\tau_{\text{sp}}(y,t)\), respectively \(\sigma_{\text{cp}}(y,t)\) and \(\sigma_{\mathbf{\text{sp}}}\mathbf{(y,t)}\) at increasing values of the spatial variable y. As expected, the oscillations' amplitude corresponding to the fluid velocity and shear stress diminishes for increasing values of y while the amplitude of normal stresses is an increasing function with respect to this variable. Consequently, the fluid velocity and the corresponding shear stress in absolute value are higher in the vicinity of the moving plate. Last Figure 10 presents the variations of \(u_{\text{Ep}}(y)\) and \(\sigma_{\text{Ep}}(y)\) at increasing values of the pressure-viscosity coefficient \(\alpha\). The fluid velocity in absolute value, as well as the normal stress, is a decreasing function of \(\alpha\). This is possible because the fluid viscosity increases for growing values of \(\alpha\) and its velocity decreases. Both entities smoothly increase from minimum values on the lower plate to the values zero, respectively two on the upper plate.
Figure 4. Time variations of the mid plane velocities
\(u_{\text{cp}}(0.5,t)\) and \(u_{\text{sp}}(0.5,t)\)for \(\text{Re} = 100,\text{We} = 1,\omega = \pi/12\) and decreasing values of \(\alpha\).
Figure 5. Time variations of the frictional forces per unit area \(\tau_{\text{cp}}(1,t)\) and \(\tau_{\text{sp}}(1,t)\) for \(\text{Re} = 100,\text{We} = 1,\omega = \pi/12\) and decreasing values of \(\alpha\).
Figure 6. Time variations of the normal stresses
\(\sigma_{\text{cp}}(0,t)\) and \(\sigma_{\text{sp}}(0,t)\) on the bottom plate for \(\text{Re} = 100,\text{We} = 1,\omega = \pi/12\) and
decreasing values of \(\alpha\).
Figure 7. Time variations of the velocity fields \(u_{\text{cp}}(y,t)\) and \(u_{\text{sp}}(y,t)\) for \(\text{Re} = 100,\) \(\text{We} = 1,\omega = \pi/12,\alpha = 0.8\) and increasing values of y.
Figure 8. Time variations of the shear stresses \(\tau_{\text{cp}}(y,t)\) and \(\tau_{\text{sp}}(y,t)\) for \(\text{Re} = 100,\) \(\text{We} = 1,\omega = \pi/12,\alpha = 0.8\) and increasing values of y.
Figure 9. Time variations of the normal stresses \(\sigma_{\text{cp}}(y,t)\) and \(\sigma_{\text{sp}}(y,t)\) for \(\text{Re} = 100,\) \(\text{We} = 1,\omega = \pi/12,\alpha = 0.8\) and increasing values of y.
Figure 10. Profiles of \(u_{\text{Ep}}(y)\) and \(\sigma_{\text{Ep}}(y)\) for \(\text{We} = 1\) and decreasing values of the pressure-viscosity coefficient \(\alpha\).
- Two isothermal motions of some IMF with power-law dependence of viscosity on the pressure between parallel plates were investigated when the gravity effects are taken into consideration.
- Analytical expressions for the dimensionless long-time solutions corresponding to these motions were established when the lower plate applies time-dependent shear stresses to the fluid.
- As a check of their corrections, the solutions of CIMF performing same motions have been recovered as limiting cases of present results using appropriate approximations of Bessel functions.
- Oscillatory behavior of these motions, phase difference between them and the influence of pressure-viscosity coefficient on the obtained solutions is graphically brought to light and discussed.
- Similar solutions for the motion of same fluids generated by the lower plate that applies an exponential shear stress \(\lbrack 1 - \exp( - t/\lambda)\rbrack S\) to the fluid have been also determined.
- Steady shear stress corresponding to this motion is constant on the entire flow domain although the corresponding velocity and normal stress are functions of y and . This constant is even the non-dimensional shear stress applied to the fluid by the lower plate.
Author Contributions:
All authors contributed equally in this paper. All authors read and approved the final version of this paper.Conflicts of Interest:
The authors declare no conflict of interest.Data Availability:
All data required for this research is included within this paper.Funding Information:
No funding is available for this research.References
- Stokes, G. G. (1845). On the theories of the internal friction of fluids in motion, and of the equilibrium and motion of elastic solids. Transactions of the Cambridge Philosophical Society, 8, 287-305. [Google Scholor]
- Bridgman, P. W. (1931). The Physics of High Pressure. The MacMillan Company, New York. [Google Scholor]
- Cutler, W. G., McMicke, R. H., Webb, W., & Scheissler, R. W. (1958). Study of the compressions of several high molecular weight hydrocarbons. Journal of Chemical Physics, 29, 727-740. [Google Scholor]
- Johnson, K. L., & Tewaarwerk, J. L. (1977). Shear behavior of elastohydrodynamic oil films. Proceedings of the Royal Society A, 356, 215-236. [Google Scholor]
- Bair, S., & Winer, W. O. (1992). The high pressure high shear stress rheology of liquid lubricants. Journal of Tribology, 114, 1-13. [Google Scholor]
- Bair, S., & Kottke, P. (2003). Pressure-viscosity relationship for elastohydro-dynamics. Tribology Transactions, 46, 289-295. [Google Scholor]
- Prusa, V. Srinivasan, S., & Rajagopal, K. R. (2012). Role of pressure dependent viscosity in measurements with falling cylinder viscometer. International Journal of Non-Linear Mechanics, 47, 743-750. [Google Scholor]
- Kannan, K., & Rajagopal, K. R. (2005). Flows of fluids with pressure dependent viscosities between rotating parallel plates. in: P. Fergola et al., (Eds.), New Trends in Mathematical Physics, World Scientific, Singapore. [Google Scholor]
- Rajagopal, K. R. (2004). Couette flows of fluids with pressure dependent viscosity, International Journal of Applied Mechanics and Engineering, 9, 573-585. [Google Scholor]
- Rajagopal, K. R. (2008). A semi-inverse problem of flows of fluids with pressure dependent viscosities. Inverse Problems in Science and Engineering, 16, 269-280. [Google Scholor]
- Prusa, V. (2010). Revisiting Stokes first and second problems for fluids with pressure-dependent viscosities. International Journal of Engineering Science, 48, 2054-2065. [Google Scholor]
- Fetecau, C., & Agop, M. (2020). Exact solutions for oscillating motions of some fluids with power-law dependence of viscosity on the pressure. Annals of Academy of Romanian Scientists: Series on Mathematics and its Applications, 12 (1-2), 295-311. [Google Scholor]
- Fetecau, C., & Vieru, D. (2020). Exact solutions for unsteady motion between parallel plates of some fluids with power-law dependence of viscosity on the pressure. Applications in Engineering Science, 1, Article ID: 100003. https://doi.org/10.1016/j.apples.2020.100003. [Google Scholor]
- Fetecau, C., & Rauf, A. (2021). Permanent solutions for some motions of UCM fluids with power-law dependence of viscosity on the pressure. Studia Universitatis Babes-Bolyai - Mathematica, 66(1), 197-209. [Google Scholor]
- Fetecau, C., & Vieru, D. (2022). Steady-state solutions for modified Stokes' second problem of Maxwell fluids with power-law dependence of viscosity on the pressure. Open Journal of Mathematical Sciences, 6, 14-24. [Google Scholor]
- Fetecau, C., Vieru, D., Rauf, A., & Qureshi, T. M. (2021). Steady-state solutions for some motions of Maxwell fluids with pressure-dependence of viscosity. Journal of Mathematical Sciences: Advances and Applications, 68, 1-28. [Google Scholor]
- Fetecau, C., Vieru, D., Rauf, A., & Qureshi, T. M. (2022). Mixed boundary value problems which describe motions of Maxwell fluids with power-law dependence of viscosity on the pressure. Chapter to be published in the book Applications of Boundary Value Problems, Nova Science Publishers, Inc. [Google Scholor]
- Karra, S., Prusa, V., & Rajagopal, K. R. (2011). On Maxwell fluids with relaxation time and viscosity depending on the pressure. International Journal of Non-Linear Mechanics, 46, 819-827. [Google Scholor]
- Zill, D. G. (2009). A First Course in Differential Equations with Modelling Applications. Ninth Edition, BROOKS/COLE, CENGAGE Learning, Australia, United Kingdom, United States. [Google Scholor]
- Fetecau, C., Rauf, A., Qureshi, T. M., & Khan, M. (2020). Permanent solutions for some oscillatory motions of fluids with power-law dependence of viscosity on the pressure and shear stress on the boundary. Zeitschrift für Naturforschung A - Physical Sciences, 75(9), 757-769. [Google Scholor]